Depuis les années 1970, une nouvelle étude morphologique est apparue : celle des villes (Haggett, 1965). « L'objet de la morphologie urbaine est la forme urbaine, forme posant d'entrée de jeu, la question de sa définition. Ce que nous ont montré les premiers travaux de morphologie. [C'est] que la forme urbaine n'est jamais une donnée a priori, elle est toujours construite, un objet d'étude construit à partir d'une [hypothétique] définition, d'une représentation [et] d'un point de vue sur [sa] forme : [sur] la forme du tissu (développée dans les trois écoles de morphologie, italienne, française et anglaise), [et sur] la forme urbaine [elle-même] comme forme des tracés (développée par les géographes allemands de l'entre-deux-guerres ; Lavedan, 1936) » (Lévy, 2005). Ainsi, pour définir morphologiquement une ville, il existe trois possibilités : (1) soit la ville est définie comme une tache correspondant généralement à une agglomération morphologique au sens de François Moriconi-ébrard (1994) ; (2) soit la ville est caractérisée par son réseau intra-urbain ; (3) soit la ville est définie par ses bâtiments (Brunhes, 1900 ; Robic ; 2003). Chacune de ces définitions fera l'objet d'un chapitre.
Si l'on définit la ville par sa tache, on s'intéresse exclusivement à son contour, à sa limite, mais comment définir ce qui fait parti de la ville et ce qui n'en fait pas parti ? Généralement, on choisit un seuil statistique basé sur une densité de population, ce qui suppose que l'on ait des connaissances sur la répartition de cette population. Cependant, si l'on ne possède aucune de ces informations, il faut utiliser un référent morphologique qui dépend de l'outil que l'on utilise. Par exemple, la télédétection ou la photographie aérienne permettent d'identifier les structures bâties, puisqu'elles ont une réflectance particulière. Par contre, si l'on caractérise la ville par son réseau intra-urbain, l'outil privilégié est sans doute le plan de la ville. Pour le faire apparaître clairement, cela nécessite une haute résolution, mais on néglige tout autre aspect de la ville : bâti dense, place, espaces verts etc. Enfin, la ville peut être identifiée grâce à la densité élevée de son bâti. Autrement dit, ici, la ville n'inclut pas les réseaux, les jardins publics ou privés, les terrasses, les places, les points d'eau, etc. Nombreux sont donc les outils permettant d'identifier le bâti : la télédétection, les photographies aériennes, les plans du cadastre, etc.
Ce chapitre va effectuer une analyse fractale de différentes taches urbaines extraites à partir des données des satellites Landsat. Il ne s'agit pas de réaliser une réflexion sur la télédétection, mais simplement d'extraire différentes taches urbaines de plusieurs villes du monde, et de les comparer grâce à l'aide d'une analyse fractale.
7.1. Extraction des données
Le site http://sedac.ciesin.columbia.edu/ulandsat/data.jsp/ fournit des données gratuites, localisées et datées des principales villes du monde. Ses images ont été analysées et prétraitées par Christopher Small (2006). Un autre site, celui d'Ann Bryant (2007), http://geology.com/world-cities/, a mis à disposition des images datant toutes de 1999. Ces deux sites ont pour source les images des satellites du programme états-uniens Landsat, et plus particulièrement de Landsat 7.
7.1.1. Les satellites Landsat
Le programme Landsat de la NASA débuta le 22 juillet 1972 avec la mise en orbite de Landsat 1. Six satellites furent lancés entre 1972 et 1999, et seuls Landsat 5 (1984) et Landsat 7 (1999) fonctionnent toujours aujourd'hui. Ces deux satellites suivent une orbite héliosynchrone à une altitude de 705 km, leur cycle orbital étant de 16 jours (Girard et Girard, 1999).
Landsat 5 possède un capteur TM (Thematic Mapper) à sept bandes spectrales (Robin, 2002). Les canaux 1, 2 et 3 captent la lumière visible, les canaux 4, 5 et 7, le proche et moyen infrarouge, et le canal 6, le rayonnement thermique. Chaque canal possède une résolution spectrale : 30 × 30 m2 pour les canaux 1, 2, 3, 4, 5, 7 et 80 × 80 m2 pour le canal 6. Toutefois, il est important de noter que chaque scène capturée (ou image) possède une résolution spatiale (taille du pixel) de 30 × 30 m2. Landsat 7 possède, quant à lui, un capteur ETM+ (Enhanced Thematic Mapper Plus). La seule différence entre TM et ETM+ est l'existence d'un canal supplémentaire (le canal 8) dit panchromatique dont la résolution spectrale est 15 × 15 m2 (Robin, 2002).
Les deux bases de données citées précédemment ont principalement pour source le satellite Landsat 7. La base de données de Christopher Small (2006) est constituée d'images filtrées. En effet, seuls les canaux 2, 4 et 7 ont été utilisés pour déterminer les structures urbaines. Chaque image possède un pixel de 30 × 30 m2, et une étendue de 30 × 30 km2. Pour plus de détail, le lecteur pourra lire l'article de Christopher Small (2005) dans lequel il détaille tous ses prétraitements. La base d'Ann Bryant (2007) est plus problématique. En effet, il n'y a aucune description des données. Il semble qu'il s'agisse d'images Landsat 7 brutes c'est-à-dire qu'elles possèdent l'intégralité de leurs canaux. Le pixel semble correspondre à 30 × 30 m2, mais l'étendue n'est pas normalisée comme dans la base de Christopher Small.
Ces deux bases sont utilisables, sous certaines conditions, dans l'optique d'une analyse fractale des taches urbaines que l'on peut extraire de ces images.
7.1.2. Les couleurs de l'urbain
Sur le site de SEDAC (SocioEconomic Data and Applications Center), organisme dont dépend Christopher Small, il est précisé que, sur chaque image traitée, l'aire urbaine peut être identifiée par les couleurs suivantes : le violet, le gris et le blanc. La végétation apparaît en vert, et l'eau en noir ou bleu foncé. Si l'on prend l'exemple de Beijing (Figure 62.a), à l'œil nu, on perçoit très bien la tache urbaine. Il serait très simple de l'extraire manuellement par l'intermédiaire d'un système d'information géographique. Toutefois, s'il faut réaliser cette tâche sur les soixante-dix huit images de la base de données de Christopher Small (2006) et sur les soixante-trois images d'Ann Bryant (2007), cela devient très contraignant. Aussi, pour traiter plus rapidement ces données, on peut utiliser une méthode de filtrage proposée par Hiba Alawad (Alawad et Grasland, 2009).
7.1.3. L'extraction de la tache urbaine
Initialement, cette méthode d'extraction semi-automatique avait été testée à des résolutions plus fines pour identifier les structures bâties dans les villes (Alawad et Grasland, 2009). Elle peut être étendue très facilement à l'extraction, grossière, d'une tache urbaine.
Il faut rappeler qu'une image est une matrice à deux dimensions, où chaque cellule (ou pixel) représente une couleur. Il existe plusieurs sortes de codage possible : le RGB, le CMYK, le niveau de gris, etc. Ici, chaque image a été codée en RGB (Red, Green, Blue). Ce qui signifie que chaque pixel possède trois bandes : une rouge, une verte et une bleue. Chaque bande possède une valeur allant de 0 à 255 : plus 16 millions de couleurs sont donc possibles.
Pour extraire le bâti, Hiba Alawad et Loïc Grasland utilisent la bande rouge ; ils se fixent un seuil, à partir des données, qui leur permet d'identifier l'intervalle dans lequel se trouvent les éléments bâtis (Alawad et Grasland, 2009). Cette méthode, très efficace, présente l'avantage de conserver l'hétérogénéité spatiale de l'image source, mais l'inconvénient de ne travailler que sur une seule bande. En ce qui concerne l'extraction des taches urbaines, la conservation de l'hétérogénéité des couleurs de l'image source apporte peu d'informations. Aussi, on peut mettre au point un filtre, très simple, qui limite cette hétérogénéité (Tonye et alii, 2000).
Le filtre est le suivant : dans chaque bande, toutes les valeurs comprises entre 0 et 99 vont être codées 0 ; toutes celles entre 100 et 199, 100 ; toutes celles entre 200 et 255, 200. Ainsi, on obtient une image possédant 27 couleurs potentielles (Figure 61), au lieu de 16 millions, ce qui permet une identification, grossière, mais efficace de la tache urbaine (Figure 62.b).
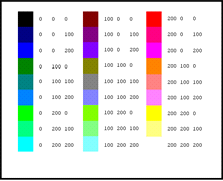

Le filtrage des couleurs ayant été effectué, il suffit d'identifier les couleurs de la tache urbaine. Dans le cas de Beijing, seule la couleur (0, 0, 100) permet d'identifier la tache urbaine. Toutefois, dans la majorité des images de Christopher Small (2006) et d'Ann Bryant (2007), il y a entre deux et cinq couleurs qui caractérisent la tache urbaine dans chacune des images. Celles-ci sont limitées à un choix parmi les dix couleurs suivantes : magenta foncé (200, 0, 200), violet (100, 0, 100), bleu gris (100, 100, 200), bleu foncé (0, 0, 100), gris (100, 100, 100), rose foncé (200, 100, 100), rouge (200, 0, 0), rouge foncé (100, 0, 0), vert gris (0, 100, 100), rose (200, 100, 100). Ce choix est contingent à chaque entité urbaine et dépend de ce que perçoit le modélisateur.
à partir de là, il est facile de convertir les couleurs choisies en blanc et les autres en noir ce qui donne le résultat final (Figure 63). Cette méthode a été appliquée aux soixante-huit images de la base de Christopher Small (2006) et aux soixante-trois images de celle d'Ann Bryant (2007). Cependant, elle ne fonctionne pas à chaque fois, seules 101 sur les 131 ont fourni une extraction convaincante. De plus, l'image obtenue comporte beaucoup de bruits, surtout aux grandes échelles.

7.1.4. Les limites de l'extraction
Plusieurs paramètres peuvent perturbés l'extraction des taches urbaines : le manque de cohérence des couleurs de l'image originale, les ombres, les nuages, la trop forte prégnance d'entités physiques (montagnes, lacs), etc. Ces éléments seraient gênants dans la construction d'une base de données représentant l'image précise d'une agglomération à une échelle donnée. Cependant, l'objectif de ces extractions étant de réaliser une analyse fractale de chaque structure urbaine, ces « éléments perturbants » deviennent de simples bruits si leur nombre et leur étendue restent limités en termes de taille. Finalement, seuls les bruits dus à la répartition des couleurs elles-mêmes peut être source d'erreur dans la mesure de la dimension fractale de la tache de l'agglomération, ce qui est le principal critère de rejet des trente images non prises en compte. De plus, les pixels isolés ne représentent pas forcément des entités bâties. Leur surnombre est visible à grande échelle dans l'analyse fractale par comptage de boîtes carrées. Puis, progressivement en allant vers les petites échelles, ce bruit est éliminé par la méthode même de l'estimation de la dimension fractale. Cette observation se matérialise par une structure multifractale dont la gamme d'échelles aux hautes résolutions s'interprète comme un bruit. De plus, l'analyse par comptage de boîtes carrées joue le rôle d'un buffer (Le Corre et alii, 2000), puisque, au-delà de l'échelle de coupure entre les deux domaines fractals, en allant vers les petites échelles, on mesure la dimension fractale de la tache urbaine, et non plus celle du bruit des grandes échelles.
Seules soixante-deux images de Christopher Small (2006) et trente-neuf images d'Ann Bryant (2007) ont pu être utilisées et utilisables pour l'analyse fractale.
7.2. Analyse fractale des données
Une dimension fractale par comptage de boîtes carrées a été réalisée pour les 101 entités urbaines retenues. Chacune d'elle présente des cas de dimensions fractales constantes dans la gamme d'échelles d'analyse (de 30 m (ou 15 m) à l'étendue de l'image).
7.2.1. Les résultats
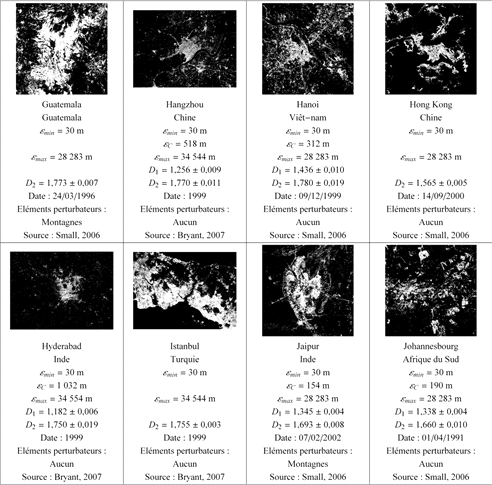
La Figure 64 présente les différentes taches urbaines et leurs caractéristiques. La première ligne donne le nom de l'agglomération ; la seconde, l'État ; la troisième, la résolution ; la quatrième l'échelle de coupure ; la cinquième, l'étendue ; la sixième, la dimension fractale observée aux grandes échelles appelée D1 ; la septième, l'estimation de la dimension fractale aux petites échelles appelée D2 ; la huitième, la date de la capture (toutes les dates étant antérieures à 1999 correspondent à une capture Landsat 5), la neuvième, les éléments perturbateurs, c'est-à-dire les entités physiques ou anthropiques ne correspondant pas à la structure urbaine qui sont, malgré tout, pris en compte dans le calcul de la dimension fractale, et la dixième, la base de données d'où provient l'image servant au calcul. D1 et D2 ne sont pas de même nature. D1 correspond à la structure fractale d'un « bruit » présent aux grandes échelles. En effet, lors de l'extraction, la tache n'est pas fermée ; elle le devient à partir de l'échelle de coupure propre à chacune des images dont la moyenne est 425 ± 47 m. Une fois que la résolution est supérieure à cette échelle de coupure, une seconde dimension fractale D2 apparaît. Cette dernière correspond à la mesure de la dimension de la tache urbaine proprement dite. Cette interprétation est étayée également par le fait que certaines villes ayant été extraites sans bruit telle que Accra, Bogota, Budapest, Buenos Aires 1, Calcutta 1, etc., n'ont pas de transition fractal - fractal. Ainsi, seules les valeurs de D2 doivent être étudiées, D1 ne renvoyant qu'au bruit de l'extraction.
Il est important de noter que certaines agglomérations sont présentes dans les deux bases de données. Tel est le cas de Buenos Aires, de Calcutta, de Lagos, de Montreal, de Mumbai, de Paris, de Perth, de Rio de Janeiro, de Santiago, de Sao Paolo, de Sydney et de Tokyo. Toutefois, la valeur de ces doubles dimensions fractales est parfaitement comparable dans la mesure où, si l'étendue est différente, la taille du pixel est comparable, car soit il est identique (30 × 30 m2), soit il n'y a qu'un facteur quatre entre la taille des pixels des agglomérations ayant des pixels plus fins (15 ×15 m2). Il est donc possible de regrouper ces données.












Si l'on considère que ces douze images en double sont indépendantes, la combinaison des estimations (valeurs et erreurs) se calcule de la manière suivante : soient wi = ![]() et w =
et w = ![]() wi alors la moyenne vaut
wi alors la moyenne vaut ![]() =
= ![]()
![]() wiDi, où Di est la dimension fractale, et l'erreur vaut
wiDi, où Di est la dimension fractale, et l'erreur vaut ![]() =
= ![]() . Si on applique cette méthode statistique, on peut proposer une estimation globale de la dimension fractale des douze villes en double (Figure 65).
. Si on applique cette méthode statistique, on peut proposer une estimation globale de la dimension fractale des douze villes en double (Figure 65).
| Agglomération | Dimension fractale corrigée |
Erreur corrigée |
|---|---|---|
| Buenos Aires | 1,766 | 0,004 |
| Calcutta | 1,759 | 0,006 |
| Lagos | 1,564 | 0,003 |
| Montreal | 1,769 | 0,007 |
| Mumbai | 1,757 | 0,004 |
| Paris | 1,820 | 0,007 |
| Perth | 1,755 | 0,006 |
| Rio de Janeiro | 1,767 | 0,004 |
| Santiago | 1,764 | 0,007 |
| São Paulo | 1,655 | 0,003 |
| Sydney | 1,628 | 0,005 |
| Tokyo | 1,798 | 0,004 |
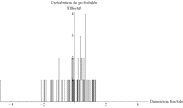
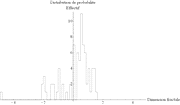
Ces corrections étant effectuées, il est possible de dresser une statistique de la dimension fractale observée pour chacune de ces agglomérations (Figure 66). On suppose que la loi des grands nombres atténue le bruit contenu dans chacune des images analysées, et qu'il s'agit d'une distribution gaussienne en première approximation. La statistique est centrée autour de la valeur 1,7 ± 0,1.
| n = 89 | ||
 |
 |
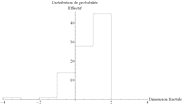 |
| Arrondi : 0,001 Moyenne : 1,723 Écart-type : 0,084 Erreur : 0,009 |
Arrondi : 0,01 Moyenne : 1,72 Écart-type : 0,08 Erreur : 0,01 |
Arrondi : 0,1 Moyenne : 1,7 Écart-type : 0,1 Erreur : 0,1 |
7.2.2. La critique des données extraites
Pour être certain que cette moyenne n'est pas biaisée par les tailles des différentes images, il faut isoler les deux sources de données et dresser leur statistique respective.
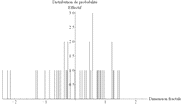
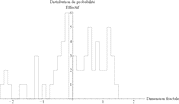
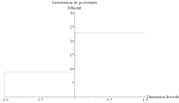
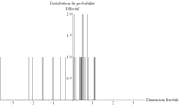
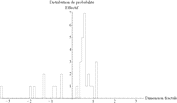
Les données de Christopher Small présentent une distribution statistique (Figure 67) analogue à la Figure 66. Il en est de même avec les données d'Ann Bryant (Figure 68). De plus, la part des deux sources différentes (1,737 et 1,705) dans la valeur moyenne (1,723) est de l'ordre de 50% (1,737 – 1,723 = 0,014 et 1,723 – 1,705 = 0,018). Autrement dit, les deux sources de données sont comparables, l'une ne domine pas l'autre.
 |
 |
 |
| Arrondi : 0,001 Moyenne : 1,737 Écart-type : 0,077 Erreur : 0,010 |
Arrondi : 0,01 Moyenne : 1,74 Écart-type : 0,08 Erreur : 0,01 |
Arrondi : 0,1 Moyenne : 1,7 Écart-type : 0,1 Erreur : 0,1 |
 |
 |
<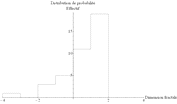 |
| Arrondi : 0,001 Moyenne : 1,705 Écart-type : 0,105 Erreur : 0,017 |
Arrondi : 0,01 Moyenne : 1,71 Écart-type : 0,11 Erreur : 0,02 |
Arrondi : 0,1 Moyenne : 1,7 Écart-type : 0,1 Erreur : 0,1 |
7.3. Interprétations
Comment expliquer cette dimension fractale constante ? Plusieurs hypothèses peuvent être formulées. Tout d'abord, la dimension fractale est peut-être liée à la localisation des taches sur l'espace terrestre. Ensuite, elle pourrait être reliée à la population contenue dans cette tache. Enfin, elle pourrait être reliée à la surface relative des taches.
7.3.1. Dimension fractale et localisation des taches
La localisation des taches mesurées (Figure 69) permet de constater qu'il n'existe aucun lien entre la répartition et les aires culturelles, même si l'on constate sur la carte quelques nids au niveau des grands foyers de peuplement (Europe, Inde, Chine et partie est des États-Unis) autour desquels les dimensions fractales sont plus faibles que ceux-ci. Autrement dit, la dimension fractale de chacune de ces taches est indépendante de sa localisation. En effet, que la ville suive un plan hippodamien ou un plan circulaire ou qu'elles apparaissent sous forme d'une tache « étoilée », la dimension fractale reste très proche de 1,7. Qu'en est-il du rapport entre la dimension fractale et de la population contenue dans cette tache ?
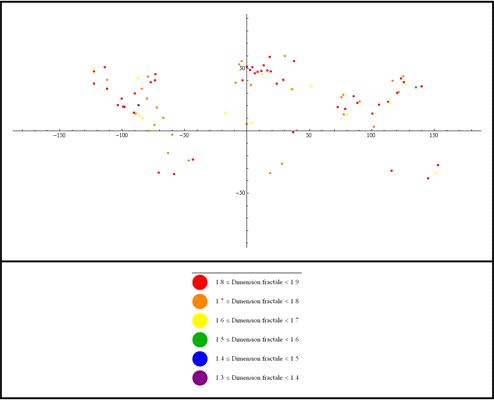
7.3.2. Dimension fractale et population urbaine
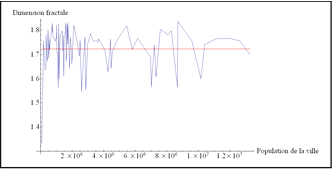
Pierre Frankhauser (1994) a montré qu'il existait des liens entre la dimension fractale et la population urbaine. Les données de la population sont issues de la base Tageo qui sera expliquée en détail dans le chapitre 16. La valeur que fournit cette base ne concerne que la ville principale, et non la totalité de la tache formant l'agglomération morphologique. Toutefois, la Figure 70 et la Figure 71 semblent indiquer l'inverse des résultats de Pierre Frankhauser : il n'existe aucun lien entre la dimension fractale et la population de la ville principale de la tache. Qu'en est-il de la dimension fractale et de la surface relative ?
| Tache | D2 | Population |
|---|---|---|
| Accra | 1.743 | 1 719 100 |
| Alger | 1.711 | 1 661 000 |
| Athènes 1 | 1.810 | 762 100 |
| Atlanta | 1.671 | 423 900 |
| Bangalore | 1.709 | 4 547 300 |
| Bangkok | 1.818 | 5 455 200 |
| Beijing 1 | 1.739 | 7 209 900 |
| Berlin | 1.752 | 3 396 300 |
| Beyrouth | 1.598 | 1 185 300 |
| Bogota | 1.689 | 6 981 500 |
| Brisbane | 1.830 | 1 598 600 |
| Brussels | 1.822 | 1 005 800 |
| Budapest | 1.833 | 1 727 300 |
| Buenos Aires 1 | 1.766 | 11 928 400 |
| Calcutta 1 | 1.759 | 4 852 800 |
| Calgary | 1.754 | 938 300 |
| Caracas | 1.714 | 1 967 800 |
| Changchun | 1.743 | 2 337 000 |
| Chennai | 1.641 | 4 466 900 |
| Chicago | 1.553 | 2 862 400 |
| Cozumel | 1.330 | 69 400 |
| Dakar | 1.572 | 2 613 700 |
| Damas | 1.719 | 1 614 500 |
| Delhi | 1.741 | 10 400 900 |
| Dhaka | 1.721 | 5 818 600 |
| Dublin | 1.713 | 1 027 900 |
| Genève | 1.756 | 181 200 |
| Glasgow | 1.696 | 1 081 800 |
| Guadalajara 1 | 1.824 | 1 672 000 |
| Guangzhou | 1.771 | 3 244 900 |
| Guatemala | 1.773 | 999 400 |
| Hangzhou | 1.770 | 1 881 500 |
| Hanoï | 1.780 | 1 420 400 |
| Hong Kong | 1.565 | 7 018 600 |
| Hyderabad | 1.750 | 3 654 900 |
| Istanbul | 1.755 | 9 592 200 |
| Jaipur | 1.693 | 2 462 500 |
| Johannesbourg | 1.660 | 1 975 500 |
| Katmandou | 1.829 | 743 300 |
| Kuala Lumpur | 1.716 | 1 410 300 |
| Lagos 1 | 1.564 | 8 682 200 |
| Le Cap | 1.744 | 2 984 100 |
| Lisbonne | 1.718 | 560 700 |
| Londres | 1.803 | 7 593 300 |
| Madrid 2 | 1.786 | 3 167 000 |
| Managua | 1.562 | 1 113 100 |
| Manaus | 1.672 | 1 615 700 |
| Melbourne | 1.765 | 3 666 000 |
| Mexico 1 | 1.836 | 8 705 100 |
| Miami | 1.709 | 380 500 |
| Monterrey | 1.828 | 1 142 900 |
| Montreal 1 | 1.769 | 3 256 300 |
| Moscou | 1.764 | 11 102 300 |
| Mumbai 1 | 1.757 | 12 622 500 |
| Munich | 1.760 | 1 241 100 |
| Nairobi | 1.758 | 2 504 400 |
| New York | 1.781 | 8 091 700 |
| Nouvelle-Orléans | 1.802 | 466 600 |
| Osaka | 1.547 | 2 596 700 |
| Paris 1 | 1.820 | 2 107 700 |
| Perth 1 | 1.755 | 1 412 900 |
| Phoenix | 1.776 | 1 409 900 |
| Port-au-Prince | 1.736 | 1 156 400 |
| Puebla | 1.797 | 1 370 800 |
| Pyongyang | 1.773 | 2 811 500 |
| Quito | 1.610 | 1 466 300 |
| Rio de Janeiro 1 | 1.767 | 6 150 200 |
| Saint-Pétersbourg | 1.718 | 4 079 400 |
| Salt-Lake-City | 1.723 | 179 900 |
| Salvador | 1.684 | 513 400 |
| San Francisco | 1.792 | 746 900 |
| San Jose | 1.642 | 340 100 |
| Santa Cruz | 1.724 | 1 196 100 |
| Santiago 1 | 1.764 | 4 434 900 |
| Sao Paolo 1 | 1.655 | 10 260 100 |
| Seattle-Tacoma | 1.781 | 767 200 |
| Seoul | 1.6 | 10 165 400 |
| Shanghai 1 | 1.700 | 13 278 500 |
| Shenyang | 1.759 | 3 527 800 |
| Stockholm | 1.781 | 1 250 400 |
| Sydney 1 | 1.628 | 4 277 200 |
| Teheran | 1.606 | 7 317 200 |
| Tokyo 1 | 1.798 | 8 294 200 |
| Toronto 1 | 1.713 | 4 551 800 |
| Vancouver 1 | 1.641 | 1 836 500 |
| Venise 1 | 1.637 | 271 800 |
| Vienne 2 | 1.755 | 1 504 100 |
| Washington DC | 1.761 | 556 500 |
| Zurich | 1.781 | 347 900 |
7.3.3. Dimension fractale et surface relative
On appelle surface relative SR le rapport entre la surface que représentent les « pixels villes » SN en mètre carré sur la surface totale de l'image ST en mètre carré.
SR =
× 100
SN et ST sont calculées à partir de la résolution de chaque image (εmin) et du nombre de « pixels villes » extrait NV (ou le nombre total de pixels NT).
SN = NV × εmin2
ST = NT × εmin2.
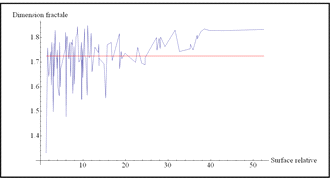
La Figure 72 montre qu'il n'existe aucun lien entre la surface relative et la dimension fractale de chacune des taches.
L'analyse fractale de l'organisation spatiale de différentes agglomérations mondiales aboutit à un résultat étonnant : pour une même résolution initiale (30 m), on observe une dimension fractale moyenne proche de 1,7, quelle que soit la forme géométrique apparente de la ville. Ce résultat est en accord avec l'hypothèse de Pierre Frankhauser d'après des calculs réalisés sur Berlin et Montbéliard (Frankhauser, 1994), sur Besançon (Frankhauser, 1998) et sur Bruxelles (Keersmacker et alii, 2004) qui proposait un modèle théorique de type « tapis de Warclaw Sierpinski » dont la dimension fractale était proche de 1,7.
De plus, cette dimension fractale constante prouve que c'est par l'étude de l'organisation multi-échelle que l'on a pu découvrir un invariant intrinsèque à l'organisation des agglomérations morphologiques que représentent les taches. La dimension fractale permet aussi de classer les différentes villes du monde en fonction de leur niveau d'organisation scalaire, mais sans que cela soit facilement interprétable. Pour preuve, il faut ajouter qu'il n'a pas été possible de relier cet indicateur à d'autres variables « plus classiques » en géographie, telles que la population de la ville principale, la surface de la tache urbaine ou la répartition même de ces taches à l'échelle du monde à nuancer en fonction des pistes évoquées ci-dessus et à vérifier. Quel est donc le processus engendrant ces morphologies si différentes d'un point de vue spatiale ? Ces processus sont-ils eux-mêmes fractales ? Enfin, l'extraction ayant été approximative, il faut vérifier ce résultat sur deux cas : l'un sur un plan de ville (Avignon), l'autre sur une répartition des bâtiments d'une ville (Montbéliard). Cela permettra également de répondre aux deux questions précédentes.
Chapitre 8. L'analyse morphologique d'images à résolution variable de la ville d'Avignon
Chapitre 9. Morphologie de l'objet « ville » défini par ses éléments bâtis
Partie 1. Échelles, limites et modèles : la forme en géographie
Partie 3. Morphométrie et analyse spatio-temporelle en géographie
Étude du cas de la répartition des châteaux dans l'espace géohistorique du nord de la France (Picardie et Artois)
