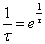Remerciements
Je remercie l'équipe archéologique du chantier de Boves.
Je remercie Laurent Nottale, Marie-Noëlle Célerier, Thierry Lehner et Amaury de Kertanguy pour leur accueil à l'Observatoire de Meudon en juin-juillet 2006 et pour tout ce qu'ils ont pu m'apprendre.
Je remercie Philippe Martin pour sa grande patience et disponibilité, sans lui ce mémoire ne serait pas ce qu'il est.
Je remercie l'UMR espace – Avignon de m'avoir si bien accueilli durant cette année universitaire 2006-2007.
1. Avant-propos
J'ai entendu parler pour la première fois de la théorie de la relativité d'échelle (Nottale, 1993, 1998) lors d'un cours de Philippe Martin en décembre 2003 à l'Université d'Artois. Qui aurait pu me dire à cette date que trois ans plus tard j'écrirai un mémoire complètement tourné vers cette théorie. Ecrire de la géographie à partir de la relativité d'échelle peut être vu comme une gageure. En effet, il s'agit d'une théorie physique, écrite en langage de physicien et pour les physiciens, ou à la rigueur pour les mathématiciens. Nous sommes donc loin du corpus géographique à l'exception de deux choses : les échelles et les formes. Je n'ai pas la prétention d'avoir tout compris de cette théorie tant elle est riche et tant ses concepts et ses idées sont profondes. Cependant, il m'est possible d'en présenter les fondements et les applications spatio-temporelles, et de montrer qu'elle a toujours été présente en filigrane en géographie, de manière informelle, et cela depuis l'émergence de l'école vidalienne !
J'avais déjà commencé cette entreprise dans mon mémoire de master 1 (Forriez, 2005). Au cours de mon premier stage archéologique à Boves (été 2004), je m'étais aperçu que la chronologique relative du château obéissait à un ordre log-périodique. Aussi, j'avais décidé de bâtir une réflexion épistémologique autour de ce constat dans ce mémoire de master 1. Elle m'a amené à commencer une double analyse : d'une part une analyse temporelle sur le site de Boves et d'autre part une analyse spatiale de la localisation des autres sites en Picardie historique (Pas-de-Calais, Somme, une partie de l'Aisne et Oise). Ces analyses ont eu deux défauts majeurs. D'abord, l'analyse temporelle n'a été réalisée que sur le château de Boves. De plus, l'analyse spatiale commencée est lacunaire et peu convaincante car elle n'a été faite que sur la carte du XXIe siècle des mottes et châteaux, carte qui était d'ailleurs incomplète. Aujourd'hui, cette carte a été remise à jour ce qui permet de préciser l'analyse. Il faudra ainsi croiser les deux pour obtenir une véritable analyse spatio-temporelle. Elle consistera à partir de l'état initial arbitrairement choisi de la répartition des mottes à l'an 1000, par exemple, et à lancer un petit programme de diffusion spatiale à partir de l'équation de Schrödinger généralisée pour voir comment la structure spatiale de la constellation des châteaux évolue, donc voir si le déploiement théorique est conforme aux données connues.
nbsp; Après mon mémoire de master 1, j'ai décidé d'occuper mon temps libre à faire avancer mon travail de recherche entrepris en 2004-2005. Il s'agit d'en achever la partie technique afin de pouvoir réaliser une simulation spatiale autrement que par les méthodes devenues classiques d'automates cellulaires ou de systèmes multi-agents. Cet objectif a été encouragé par ma rencontre avec Laurent Nottale en janvier 2006. J'avais des doutes qu'en tant à ma maîtrise de l'outil mathématique et à la validité de ce que j'avais entrevu. Finalement, il s'est avéré que j'avais envisagé par intuition une voie fructueuse.
Aussi, pour me donner les moyens de cette recherche, j'ai décidé de faire un stage avec Laurent Nottale en juin-juillet 2006 à l'Observatoire de Meudon. Ce fut un grand moment pour moi. J'ai vu comment fonctionne la recherche française et ce qu'est réellement le métier de chercheur. J'ai ainsi décidé de poursuivre dans ce mémoire de master 2 cette recherche passionnante sur la relativité d'échelle et sur son utilité et de son application en analyse spatiale, et plus généralement en géographie.
Dans ce travail, je veux simplement essayer d'établir un recueil suffisamment approfondi sur un corpus de méthodes dispersées dans plus de 300 ouvrages (si on se limite à la bibliographie française) ! Ainsi, une très importante synthèse sur le devenir, sur les théories, sur les concepts et sur l'application des sciences a été entreprise, et ce, pour satisfaire à deux objectifs : (1) montrer que la science, au sens général, vit vraisemblablement un moment crucial de son évolution ; (2) introduire l'ensemble des outils à la disposition des archéologues, des géographes, et peut être des historiens afin qu'ils puissent analyser plus en profondeur leurs résultats dans le cadre d'un espace-temps, et perfectionner les méthodes qu'ils utilisent.
Pour conclure, je tiens à préciser que ma formation d'historien m'incite plus facilement à prendre des exemples dans des espaces historiques, donnant ainsi en plus de la dimension spatiale, une dimension temporelle non négligeable, comme c'est le cas dans l'application de Boves. Toutefois, d'autres exemples seront développés. Cela étant, cet opus est purement épistémologique et technique. Il présente peu d'exemples et de cas concrets, ceux-ci étant réservés pour ma thèse.
2. Introduction générale
L'analyse spatiale a déjà une cinquantaine d'années. Elle a su faire progresser la géographie vers une science quantitative. Cependant, il faut reconnaître qu'elle manque toujours d'une certaine cohérence. De nombreux géographes ont testé un faisceau de méthodes quantitatives différentes sur l'espace géographique, et ils ont réussi, par ce biais, à analyser ce dernier. Toutefois, ces méthodes et outils allant de la mécanique quantique à la mécanique newtonienne, en passant par des analyses statistiques comme les analyses en composantes principales ou les analyses factorielles de correspondance, n'offrent pas la possibilité de démarquer clairement la géographie des autres disciplines. En effet, d'une part, ces méthodes ont « marché », mais on ignore pourquoi. L'exemple type renvoie bien sûr aux automates cellulaires ou aux systèmes multi-agents. D'autre part, elles appartiennent à des théories non géographiques, en soi, et qui le restent, même si elles ont fait leur preuve en géographie. Ce mémoire a pour objectif de proposer une tentative de clarification sur la causalité profonde de l'organisation spatiale de l'interface terrestre (formes naturelles, formes anthropiques aux échelles moyennes) dont la géographie à la charge de l'étude. Il entre donc dans le projet de l'étude des formes en géographie comme élément structurant de la discipline, à la lumière des théories transdisciplinaires de la morphogenèse développées depuis les années 1980.
Le problème levé semble si important qu'il tend à recouvrir, à lui seul, toutes les autres connaissances. Dans cet effort de conciliation, il faut distinguer synthèse, fusion et recomposition. Il ne s'agit ici ni de faire une synthèse, ni d'effectuer une fusion des connaissances acquises autour de l'immense thématique qu'est la complexité. Il s'agit de réaliser une recomposition des échanges entre les différentes disciplines pour construire des objets scientifiques communs (fig. 1).
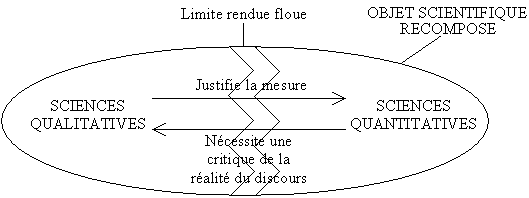
La relativité d'échelle est une extension à partir de principes premiers de la géométrie fractale. Elle a déjà permis de nombreuses applications dans différents domaines (physique, biologique, économique, etc.). De ce fait, la compréhension de l'espace terrestre à la lumière de la relativité d'échelle pourrait donner une force conceptuelle supplémentaire à tous les travaux géographiques antérieurs, et particulièrement ceux de l'analyse spatiale. Cependant, ce mémoire ne doit pas être pris comme une rupture, mais comme un complément théorique qui m'apparaît indispensable pour mieux fonder la géographie en tant que science autonome et originale.
Les essais antérieurs de Roger Brunet ou de Bernard Claval par exemple, ont toujours été problématiques dans la mesure où, pour considérer une localisation dans l'espace géographique, il fallait systématiquement faire appel ou renvoyer aux connaissances des autres sciences telles que l'économie, l'histoire, la sociologie, l'ethnologie, le droit, la géologie, la biologie, la physique, la chimie, les mathématiques pour ne citer qu'elles. Au final, la géographie spatiale est un melting pot de sciences, faisant de la géographie une discipline « carrefour ». La géographie se trouve donc être une science de synthèse, à la croisée de ce que d'autres sciences ont développé sur la localisation dans l'espace ! C'est le problème de la causalité interne et externe qu'a défini Philippe Martin (2004a). Le dualisme est le suivant : la dimension spatiale est-elle structurelle et causale, ou est-elle une conséquence attendue de la dynamique économique, sociologique, politique, ethnologique, etc. ? Dans le premier cas, le champ de la géographie peut lui être propre et est original ; alors que dans l'autre, la géographie n'est qu'une synthèse ou un « carrefour » d'autres discours, et dans ce cas une individuation ne peut être envisagée qu'au niveau des conséquences des règles et fonctionnements des métathéories dont la géographie dépendrait ; ce qui est peu.
En conséquence, tout se résume presque à savoir comment on peut objectiver les formes en géographie. Quelques éléments seront envisagés dans ce mémoire pour répondre à cette question. Il faut rappeler qu'une série de tests a permis d'expérimenter la pertinence de l'utilisation de la relativité d'échelle comme outil théorique de base pour fonder la géographie en tant que science des formes. Les quelques résultats obtenus sont plutôt convaincants (Forriez, 2005 ; Forriez, Martin 2006), même s'ils restent largement prospectifs.
Ainsi, une réflexion en quatre parties peut être proposée pour traiter cette vaste question. La première partie fera le point sur ce que sont les sciences de la complexité et sur la place que la géographie tient, ou plutôt devrait y tenir. La seconde partie fera une mise au point sur le concept d'échelle en géographie. La troisième partie présentera rapidement la théorie fractale et la relativité d'échelle. La quatrième partie développera au final quelques applications de ces théories de la complexité en géographie.
3. Géographie et complexité
Les géographes se sont intéressés relativement tôt à la complexité (Pumain et alii, 1989 ; Frankhauser, 1994 ; Dauphiné, 1995), mais tous ont vraisemblablement rencontré une difficulté : l'immense complexité de la formalisation mathématique qui n'appartient que peu à leur culture dont on sait qu'elle est encore largement littéraire. Aussi, se sont-ils contentés de fonder une série de réflexions épistémologiques pour guider la communauté des géographes sur cette voie. Malheureusement, elles n'ont fait guère école. La diffusion de ces concepts reste très restreinte car il faut bien l'avouer, ils sont très difficiles à comprendre. Cette partie a deux objectifs. D'une part, elle cherche à repositionner le débat de la complexité dans son contexte historique et à redonner des définitions plus ou moins précises autour de ce thème. D'autre part, cette partie essayera de lancer quelques pistes pour réinsérer la complexité au cœur du débat géographique contemporain.
Pour ce faire, il faudra commencer pour redéfinir ce qu'est l'épistémologie et à quoi elle sert. Puis, à partir de ces définitions, il s'agira de définir les principaux cadres doctrinaux qui ont alimenté le débat au sein de l'école géographique française. Et enfin, il faudra rappeler quelques définitions et repositionner la thématique de la complexité au sein des sciences, et particulièrement de la géographie française.
3.1. Eléments d'épistémologie
3.1.1. Philosophie, science et sciences
« A l'origine, philosophie et science étaient confondues. La connaissance, la réflexion sur la démarche scientifique en général, ou sur les progrès de chacune des sciences, relevaient du domaine des philosophies. La séparation du domaine scientifique devait amener un glissement de la signification des termes, qui aboutit aujourd'hui à une confusion regrettable » (Grawitz, 2001, p. 7).
La philosophie englobe toutes les sciences particulières qui ne sont qu'une portion limitée de la réalité. Les sciences particulières partent de présuppositions. La méthode et l'objet de la philosophie ne sont pas fixés par avance, mais elles les déterminent à chaque fois de nouveau. Emmanuel Kant a proposé de regrouper la philosophie en quatre thèmes. Que puis-je faire ? (Métaphysique) Que dois-je faire ? (Morale) Que m'est-il permis d'espérer ? (Religieux) Qu'est-ce que l'homme ? (Anthropologie)
L'épistémologie est « l'étude critique des principes, des hypothèses et des résultats des diverses sciences, destinée à déterminer leur origine logique, leur valeur et leur portée objective » (Lalande, in Grawitz, 2001, p. 8)l'origine, il s'agit d'une discipline philosophique. L'épistémologie est la synthèse de la gnoséologie (ou théorie de la connaissance) et de la philosophie des sciences. Elle étudie les connaissances, surtout dans une optique de comprendre les processus menant à la connaissance d'une science, prise ici dans le sens de savoirs. Après Gaston Bachelard qui fut le dernier philosophe à avoir eu une connaissance totale des sciences, l'épistémologie est entrée, plus ou moins, dans les différentes disciplines. La géographie semble être la science qui a le plus développée cette approche car le géographe sait que les apparences sont souvent trompeuses. Cela étant, il existe plusieurs définitions servant de socle commun.
La science offre des définitions multiples et variées mais aucune d'entre elles n'est satisfaisante. La science est « l'usage de démontrer ce que l'on affirme, c'est-à-dire de déduire des principes certains et immuables par voie de conséquences légitimes » (Wolff, in Grawitz, 2001, p. 22). Cette définition met fin au surnaturel dans les sciences. En effet, la science « est la connaissance méthodique dont le contenu, d'une manière contraignante est à la fois certain et universellement valable » (Jaspers, in Grawitz, 2001, p. 23). Cependant, il est clair que la science désigne un ensemble de connaissances plus ou moins universelles et plus ou moins vérifiables, obtenues grâce à un savoir-faire qui sont établies par l'intermédiaire d'un discours se décomposant en trois champs : le champ phénoménal, le champ théorique et le champ ontologique. Seuls le champ phénoménal et le champ ontologique sont clairement définis. Le champ théorique apparaît bizarrement comme un champ « fourre-tout » : c'est ce qui n'est ni phénoménal ni ontologique. Enfin, il faut remarquer que la science est une variable historique, ce qui signifie que l'on peut accepter plusieurs définitions par rapport à ses strates. Ici, il s'agit de développer bien évidemment la définition la plus récente possible.>
Cependant, il faut distinguer la science des sciences. La science renvoie à la théorie de la connaissance c'est-à-dire à la totalité de ce que l'on peut connaître, alors que les sciences renvoient à l'idée d'un découpage dans cette connaissance. À travers les siècles, il y eut de multiples découpages de la science. Le découpage du Moyen Age, par exemple, ne distingue que sept disciplines dont quatre majeures et trois mineures. Aujourd'hui, le découpage date du XIXe siècle. Il s'est affirmé au début du XXe siècle avec le développement du réductionnisme. Ainsi, les sciences se sont multipliées. Le savoir se décline désormais en disciplines académiques et en sous-disciplines. En ce début du XXIe siècle, le découpage est devenu si fin que l'on ne sait plus vraiment à quelle grande discipline appartient telle sous-discipline, ou bien on ne comprend pas pourquoi dans telle science on trouve telle sous-discipline, alors qu'on pourrait la ranger dans la science voisine !
De plus, la distinction entre sciences et humanités est récente dans l'histoire de la pensée occidentale. Au début du XVIIe siècle, les « lettres » désignent tout le domaine de la connaissance. La rupture est consacrée, en France par exemple, par la création en 1852 du Baccalauréat ès-sciences. Toutefois, la pensée qui va définitivement séparer sciences et humanités, c'est le marxisme. Les penseurs marxistes opposent les sciences quantitatives et les sciences qualitatives, le postulat étant que les premières seraient plus scientifiques que les secondes, donc plus utiles. Le développement de la pensée utilitariste tout au long du XXe siècle, dont la consécration est la société de consommation, aboutit à une sorte de « blocage psychologique » qui maintient fortement cette distinction. La comparaison entre le budget d'une faculté de mathématique et une faculté de géographie en France illustre bien ce propos. Toutefois, l'idéologie communiste est tombée en 1991. De ce fait, cette distinction peut-elle toujours se maintenir en ce XXIe siècle ? Par ailleurs, la notion d'utilité est ambiguë dans la mesure où il existe bien sûr une utilité immédiate liée à la matérialité du monde, à la production de produits, à l'échange mais il y a aussi une utilité différée et moins visible liée par exemple aux cadres de pensée qui permettent le fonctionnement des sociétés de consommation en particulier. Que l'on songe par exemple à un certain nombre de règles traditionnelles liées au statut de l'enfant et de la femme…
La pensée marxiste a consacré une division de la connaissance en deux sciences : les sciences « dures » et les sciences « molles » - ces dernières n'atteignant jamais le même niveau de scientificité que les premières - ou plus exactement la division entre les sciences utiles et les sciences inutiles. Cette fracture a été accentuée, pour ne pas dire consommée, par la Guerre froide. Pourquoi cette division ? C'est d'abord pour satisfaire le besoin utilitariste de la pensée libérale occidentale, repris avec véhémence (et de façon apparemment paradoxale) par la pensée marxiste. Cette division semble avoir disparu avec la chute de l'Union des Républiques socialistes soviétiques ! Certains, comme Stephen Jay Gould (2005), prétendent que la séparation n'a jamais existé.
Cependant, Stephen Jay Gould (2005) déplore cette distinction. Il qualifie les sciences de « renard » et les humanités1 de « hérisson ». Le renard est rusé, l'hérisson est tenace. Stephen Jay Gould (2005) démontre que le conflit entre les sciences et les humanités est un « pseudo-conflit » (p. 31). En effet, les termes « sciences » et « humanités » ne peuvent être employées pour désigner des entités suffisamment stables, engagées dans une lutte raisonnablement continue entre des positions intellectuelles durables et bien affirmées » (Gould, 2005, p. 92). La dichotomie est trop simpliste. « Le concept même d'opposition entre science et humanité n'est qu'une négation absurde de nos capacités mentales et notre complexité – piège non moins néfaste aux potentialités humaines que nos dérisoires efforts passés pour maintenir séparées et inégales des races qui n'existent pas » (Gould, 2005, p. 121). De plus, Stephen Jay Gould insiste sur le danger du « chiffre 2 » pour le raisonnement. Il dénonce « notre déplorable tendance à réduire toute situation complexe à une dichotomie conflictuelle » (Gould, 2005, p. 120). Il faudrait, selon lui, développer des raisonnements ternaires réduisant cette dichotomie.
Quoi qu'il en soit, l'ambiguïté du terme science demeure. Au sens étroit, il ne concerne que « l'ensemble de connaissances établi de façon systématique, à référence universelle et susceptible d'être vérifiée » (Grawitz, 2001, p. 25) c'est-à-dire les sciences physiques et naturelles. Au sens large, si on reprend la définition de Karl Jaspers, le terme désigne également les humanités. « C'est le souci de rigueur, non l'utilisation abusive de termes scientifiques, qui permettra aux sciences humaines d'accéder au statut de science » (Grawitz, 2001, p.8). Il semblerait que les sciences de l'homme seraient une réponse à la crise provoquée par les découvertes militaires et les dégâts écologiques des sciences au sens étroit. Les sciences de l'homme cherchent à comprendre le passé, et à partir de là, essayer de prédire l'avenir. Claude Lévi-Strauss (1908- ?) précise que sciences humaines et sciences sociales sont synonymes. De ce fait, on peut supposer que sciences de l'homme englobent les sciences humaines et sociales. Jean Piaget (1896-1980) propose une distinction intéressante : les sciences « nomothétiques » qui cherchent à dégager des lois ou des relations quantitatives (la psychologie scientifique, la sociologie, l'ethnologie, la linguistique, l'économie, la démographie…). Toutes ces sciences utilisent soit des méthodes d'expérimentation directe, soit d'expérimentation au sens large d'observation systématique. Les sciences historiques reconstituent le déroulement de la vie sociale au cours des temps. Les sciences juridiques et philosophiques constituent les deux dernières catégories de Jean Piaget. Il est important de constater que les sciences sociales ne sont pas encore arrivées à construire une théorie de l'Homme, leur permettant d'intégrer l'ensemble des phénomènes observés.
Enfin, la science est une croyance. De ce fait, une science a besoin d'un projet disciplinaire tel que l'avait défini Gaston Bachelard (1934). Ce projet la caractérise et la différencie des autres. « Au-dessus du sujet, au-delà de l'objet immédiat, la science moderne se fonde sur le projet. Dans la pensée scientifique, la méditation de l'objet par le sujet prend toujours la forme du projet » (Bachelard, 1934, p. 15). En effet, les différentes sciences se partagent les objets d'étude qui sont les fondements de la manière de penser la science, c'est-à-dire un moyen matériel de développer une hypothèse de recherche. L'hypothèse est une proposition de réponse à la question posée qu'il faut vérifier, tester. La définition de l'objet d'étude doit entrer dans le projet scientifique de la science envisagée. Dans nos civilisations occidentales, la définition d'objet d'étude repose essentiellement sur les quatre causes d'Aristote : la cause matérielle, l'objet existe, la cause efficiente, l'objet est issu d'une dynamique, la cause finale, l'objet a un but à atteindre et la cause formelle, cet objet est perçu par exemple. Pour René Thom, le but de la science est de « réduire l'arbitraire de la description » lié à la perception (1974, p. 276-277).
Toujours dans le domaine de la croyance, on peut noter que « […] le phénomène le plus intéressant c'est qu'aujourd'hui la science joue le rôle tenu dans le passé par la religion, en ce sens la science est aujourd'hui porteuse des espérances eschatologiques de l'humanité » (Thom, 1983, p. 16). « Nos sociétés se tournent vers les scientifiques comme les anciens se tournaient vers les oracles pour avoir des avis sur leurs inquiétudes… quelquefois soulevées par les scientifiques eux-mêmes » (Sapoval, 1997, p. 19). « L'expertise scientifique est la demande, faite à des « savants », de fournir des réponses techniques de société, réponses dont le contenu peut influencer des décisions politiques, juridiques ou même éthiques » (Sapoval, 1997, p. 19). Toutefois, une expertise n'est pas une recherche car elle se fait dans l'urgence à partir des théories que l'on croit être justes. Le problème de la croyance scientifique est pourtant sensiblement différent de celui de la croyance religieuse. En fait, il s'agit d'une croyance issue de méthodes d'analyse différentes évoluant au cours du temps, tandis que les croyances religieuses sont basées sur une différence de dogmes, posés à l'origine de cette religion. Pourtant, il existerait une guerre entre la science et la religion. Pour Stephen Jay Gould (2005), le conflit entre science et religion ne se serait jamais posé ! « La « religion », en tant qu'entité cohérente, ne s'est jamais opposée à la « science », que ce soit sur des idées générales ou sur des points de détail » (Gould, 2005, p. 41). La dichotomie science/religion est un mythe, car les pouvoirs laïques ont parfois su se montrer plus intolérants que les religions. Cependant, le relativisme du postmodernisme est néfaste car il alimente la pseudo – « guerre des sciences ».
Albert Einstein avait pourtant mis en garde l'humanité : « prenez garde à ne pas faire un dieu de votre intelligence ; elle a… des muscles puissants, mais aucune personnalité » (in Stewart, 1997, couverture). Les marxistes auraient, sans doute, souhaité faire des sciences « dures » une nouvelle religion, qui ne laissait aucune place à l'incertitude. La croyance ne fait pas partie de la science, mais depuis une trentaine d'années, la croyance a ressurgi dans les sciences : on a cru au chaos, ou on n'y a pas cru. Le problème, c'est que même en démontrant que le chaos existe, nombreux sont ceux qui répondent : « je suis convaincu par votre démonstration, je la respecte, mais je n'y crois pas ». Le verbe « croire » est choquant. La frontière entre science et religion serait-elle plus floue que ce que la raison admet ! Une démonstration est soit vraie, soit fausse, et pas partiellement vraie ou partiellement fausse. Aucune croyance ne doit s'y immiscer quelle soit laïque ou religieuse dans les sciences. Pourtant, et c'est un sentiment humain, on a besoin de croire en quelque chose, en un idéal, mais cette croyance a-t-elle sa place dans la science ? Certainement pas, et ce qu'elle soit « dure » ou « molle », seule la froideur des faits compte, qu'on le déplore ou non. C'est ainsi qu'aux yeux des théories économiques de l'innovation ou de la productivité, la science doit être finalisée. Cependant, tous les domaines scientifiques ne peuvent pas être finalisés. C'est le cas de la morphogenèse qui va particulièrement nous intéresser. Peut-on prétendre à l'inutilité de cette recherche ? Un paradoxe se crée puisqu'une recherche ne peut devenir utile uniquement lorsque l'on a pu mener cette recherche. La crise relative des sciences modernes s'inscrit dans la crise économique débutée en 1973. Par conséquent, une recherche doit aujourd'hui être finalisée, sinon elle ne trouvera pas de financement. Cependant, certaines recherches sont difficilement définissables, mais importantes pour l'avenir de l'humanité. C'est un cercle vicieux connu qui empêche l'innovation scientifique dans les domaines fondamentaux.
Par ailleurs, les sciences modernes (fig. 2) distinguent les sciences empiriques qui décrivent, explorent, expliquent, prévoient à partir de l'expérience scientifique ou humaine et les sciences rationalistes qui sont marquées par une logique interne exceptionnelle.
SCIENCES EMPIRIQUES | SCIENCES RATIONALISTES | |
|---|---|---|
Sciences de la nature | Sciences de l'homme | |
Physique | Sociologie | Mathématiques |
Psychologie | ||
3.1.2.1. Les phénomènes
Les phénomènes sont des occurrences spatio-temporelles qui affectent un observateur par ses sens. Elles sont étudiées par ce que l'on appelle la phénoménologie. Cependant, la phénoménologie n'a rien de scientifique : c'est une doctrine philosophique. Elle a été développée au début du XXe siècle par Edmond Husserl (1859-1938). Elle est née d'une contestation du kantisme et de la psychologie de l'école de Warzbourg. Elle est hostile à l'idéalisme et à l'empirisme, lié au développement scientifique et industriel. « Même les matériaux recueillis dans l'observation empirique sont construits, au lieu d'être simplement vécus. La phénoménologie se veut une méthode de retour aux choses elles-mêmes, dans les descriptions, en dehors de toute conceptualisation. Il s'agit d'une « eidétique » ou « science des essences » qui repose avant tout sur l'intuition. Comment se situe l'individu par rapport à cet objet vécu ? » (Grawitz, 2001, p. 11).
La phénoménologie est à l'origine des diverses théories existentialistes. Elle insiste sur la supériorité du vécu, du subjectif sur les constructions conceptuelles du champ théorique. « Toute science est avant tout l'étude d'une phénoménologie » (Thom, 1983, p. 5). La source d'une science est bien une phénoménologie, mais le but de la science est de chercher à la dépasser. Aussi, les problèmes de la connaissance sont étroitement liés aux différentes positions philosophiques.
3.1.2.2. La méthode et les techniques
Il ne faut pas confondre la méthode et les techniques. Pour faire simple, la méthode est un ensemble de techniques, et la technique sans méthode ne suffit pas. Méthode et techniques ne valent rien si on ne se pose pas les bonnes questions.
3.1.2.2.1. La méthode
« Le propre de la méthode est d'aider à comprendre au sens le plus large, non les résultats de la recherche scientifique, mais le processus de recherche lui-même » (Kaplan, in Grawitz, 2001, p. 15). La méthode est l'ensemble des techniques permettant d'une part l'objectivation des phénomènes observés et d'autre part de les transformer en faits avérés. C'est une notion ambiguë. « Jean Piaget (1967) remarque qu'elle n'est pas une branche indépendante, car les problèmes d'épistémologie et de logique posent constamment des questions de méthode » (Grawitz, 2001, p. 15). On peut toutefois distinguer quatre types de méthodes.
(1) La méthode au sens philosophique est constituée de l'ensemble des opérations intellectuelles par lesquelles une discipline cherche à atteindre les vérités qu'elle poursuit, les démontre, les vérifie. Cette conception de la méthode dans le sens général de procédure logique, inhérente à toute démarche scientifique, permet de la considérer comme un ensemble de règles indépendantes de toute recherche et contenu particulier, visant surtout des processus et formes de raisonnement et de perception, rendant accessible la réalité à saisir.
(2) La méthode comme étant une attitude concrète vis-à-vis de l'objet dicte des façons concrètes d'envisager ou d'organiser la recherche, mais ceci de façon plus ou moins impérative, plus ou moins précise, complète et systématisée. Toutes les méthodes n'influencent pas de la même manière, les mêmes étapes de la recherche.
(3) La méthode liée à une tentative d'explication se rattache plus ou moins à une position philosophique. Elle peut influence telle ou telle étape de la recherche. Ces méthodes visent avant tout un schéma explicatif, qui peut être plus ou moins étendu et se situer à un niveau de profondeur très différent.
(4) La méthode liée à un domaine particulier comporte une manière de procéder qui est propre à un domaine donné comme la méthode historique. Dans ce cas, la méthode se confond avec la théorie, or la théorie définit plutôt le « quoi ? » alors que la méthode devrait définir plutôt le « comment ? ».
3.1.2.2.2. Les techniques
Toute recherche ou application de caractère scientifique doit comporter l'utilisation de procédés opératoires rigoureux, bien définis, transmissibles, susceptibles d'être appliqués à nouveau dans les mêmes conditions, adaptés au genre de problèmes et de phénomènes en cause : ce sont là des techniques. Le choix de ces techniques dépend de l'objectif poursuivi, lequel est lié lui-même à la méthode de travail, qui est à l'origine de la confusion des termes technique et méthode. La technique est une réponse à un « comment ». C'est un moyen d'atteindre un but, mais qui se situe au niveau des faits ou des étapes pratiques. La technique représente les étapes d'opérations limitées, liées à des éléments pratiques, concrets, adaptés à un but défini, alors que la méthode est une conception intellectuelle, coordonnant un ensemble d'opérations, en général plusieurs techniques. Les techniques ne sont que des outils, mis à la disposition de la recherche et organisés par la méthode dans ce but.
3.1.2.3. Les faits
« L'observation scientifique [des phénomènes] est toujours une observation polémique » (Bachelard, 1934, p. 16). En effet, celle-ci entraîne une hiérarchisation des phénomènes qui est ensuite objectivées par une méthode, c'est dire que l'on reconstruit le réel pour obtenir un fait ! Les faits sont donc des constructions obtenues par une méthode d'objectivation scientifique.
3.1.3. Le champ théorique
C'est la mise en relation des faits entre eux, c'est-à-dire la recherche des causes qui les ont produits. Sa construction se fait en deux étapes. D'abord, on établit des principes premiers par différentes observations expérimentales. Puis, on définit des concepts, des modèles, le tout formant une théorie.
3.1.3.1. Les principes premiers
Le champ théorique a besoin de principes dits premiers, c'est-à-dire de principes que le chercheur est obligé de poser et d'admettre sans avoir à les démontrer. Cela montre que le champ théorique n'est jamais premier : il est toujours précédé du champ phénoménal à partir duquel ces principes premiers ont pu être posés. Ces principes sont d'abord littéraires, puis peuvent être exprimés de manière mathématique. Toutefois, il ne faut pas confondre principes et axiomes. En effet, rechercher des axiomes en géographie n'aurait aucun sens car il s'agit d'un terme réservé aux mathématiques. En effet, « les axiomes sont des faits mathématiques considérés comme évidents et que nous ne tentons pas de déduire de principes plus simples » (Chaitin, 2006, p. 70-76). Ensuite, une série de règles générales qui fonctionnent universellement, est démontrée à partir de ces principes premiers. En mathématique, on les appelle théorème, en informatique, résultat, dans les autres disciplines, théorie, tout simplement. La recherche de ces règles correspond à un double objectif : la prédiction ou la rétroprédiction, ainsi que la compréhension. Autrement dit, l'impression de maîtriser les phénomènes que l'on a pu, que l'on peut ou que l'on pourra observer.
Cependant, les axiomes peuvent être réfutés. C'est le cas, par exemple, du cinquième axiome d'Euclide. « Un des grands succès mathématiques du XIXe siècle fut la découverte de la géométrie hyperbolique. Il s'agit d'une géométrie où l'axiome des parallèles est faux. Les axiomes restant de la géométrie euclidienne permettent de démontrer que, étant donné une droite et un point en dehors de celle-ci, il existe au moins une parallèle à la droite passant par le point (la perpendiculaire à la perpendiculaire). L'axiome des parallèles stipule qu'il existe une seule parallèle ; sa négation consiste donc à supposer qu'il en existe plus d'une » (Odifreddi, 2004, p. 46). Le XXIe siècle sera celui de la géométrie fractale. D'autres axiomes peuvent être partiellement réfutés dans certain cas bien précis. C'est le cas du principe de continuité dans le cadre du chaos ou des fractales. « L'hypothèse du continu est indépendante de la théorie des ensembles : elle ne peut être ni prouvée ni […] réfutée » (Odifreddi, 2004, p. 64).
3.1.3.2. La problématique, les raisonnements et les logiques
« Le raisonnement, base de connaissance implique […], une certaine relation entre un sujet et un objet. » (Grawitz, 2001, p. 3) Le sujet englobe l'objet. Le sujet est un thème c'est-à-dire une généralité. Quant à l'objet, il s'agit d'un concept c'est-à-dire une définition d'un mot particulier. Le raisonnement est le lien entre le sujet et l'objet. Cette présentation de la distinction fondamentale est appelée la division platonicienne. Elle pose deux problèmes : comment différencier l'objet, le sujet et le raisonnement ? Quelle est la validité de la logique ?
3.1.3.2.1. La logique
Aristote (384-322 a.-C.) ne s'occupe pas de savoir si le raisonnement est vrai ou faux : s'il est logique, il est valable. C'est la logique formelle. Elle est indépendante du contenu c'est-à-dire de toute affirmation concrète. La logique formelle pose en d'autres termes le problème de la relation complexe entre la vérité et la réalité. « En éliminant le contenu objectif, historique, pratique et social de la connaissance, la logique formelle se transforme en pensée formaliste » (Grawitz, 2001, p.4). Toutefois, la logique soulève deux difficultés : le rejet du langage ordinaire comme support de la logique et le rejet du raisonnement commun des êtres humains.
Aristote fonde la logique. Cependant, ce sont George Boole, Augustus de Morgan et Gottlob Frege qui ont fondé l'alliance entre la logique et les mathématiques. Ainsi, aujourd'hui, la logique se décompose en trois composantes : les mathématiques pour le calcul, la philosophie pour la croyance et la recherche de la vérité et l'informatique pour la simulation, au sens de la théorie des processus de calcul.
On peut résumer la logique en quatre opérateurs (fig. 3).
| La négation | Non |
| La conjonction | Et |
| La disjonction | Ou |
| L'implication ou le conditionnel | Si… alors |
« Si… alors » est une vérité conditionnelle. « Si » est appelé l'antécédent, « alors » le conséquent. Son utilisation engendre le célèbre paradoxe du Menteur qui a été énoncé par Eubulide de Mégare (IVe siècle a.-C.) : lorsque l'antécédent est vrai, le conséquent est vrai. Cependant, lorsque que l'antécédent est faux, le conséquent peut être vrai puisqu'il s'agit d'une logique formelle : c'est la relation de pertinence. Désormais, on peut définir l'équivalence qui formule par une double vérité conditionnelle : si A alors B et si B alors A ; A et B sont pertinents.
Le Moyen Age établit également quatre types de proposition logique :
A dit Universelle affirmative : tout X est M ;
E dit Universelle négative : aucun X n'est M ;
I dit Particulière affirmative : quelque X est M ;
O dit Particulière négative : quelque X n'est pas M.
En 1931, Kurt Gödel (1906-1978) démontra le théorème d'incomplétude « selon lequel toute théorie mathématique suffisamment riche, contient, lorsqu'elle est cohérente, des énoncés qui y sont indécidables, c'est-à-dire qui ne peuvent y être ni prouvés ni réfutés » (Dubucs et Sandu, 2005, p. 2-5). Ce théorème est fondamental car il nous fait comprendre que la mathématisation et sa logique contiennent des limites. Il « montrait pour la première fois qu'aucun système d'axiomes ne peut à lui seul prouver toutes les vérités mathématiques » (Chaitin, 2006, p. 70-76). Il démonte un mythe scientifique établi par Galilée 300 ans plus tôt ! « On a montré que dans tout système fini d'axiomes, il existe une infinité d'énoncés mathématiques vrais qui ne peuvent y être prouvés » (Chaitin, 2006, p. 70-76). En effet, ce théorème exprime que « la cohérence de n'importe quelle théorie qui contient des nombres entiers ne peut être démontrée de l'intérieur de la théorie elle-même. En d'autres mots, aucune théorie qui prétend fonder la mathématique n'est en mesure de s'auto-justifier mais au contraire elle est contrainte à chercher une justification en dehors d'elle-même. En particulier, aucune théorie de ce genre qui soit cohérente ne peut être complète, au sens de pouvoir démontrer toutes les vérités mathématiques exprimables dans son langage, et l'une des vérités qu'elle ne peut démontrer est précisément sa propre cohérence. Pour cette raison, le résultat de Gödel fut appelé théorème d'incomplétude » (Odifreddi, 2004, p. 48). Par conséquent, « la signification des résultats de la logique mathématique demande une analyse philosophique » (Dubucs, Sandu, 2005, p. 2-5). Autrement dit, si certaines humanités, comme la géographie, mathématisent leur propos, il faut qu'elles prennent conscience de la limite philosophique, et non scientifique, de leur discours mathématisé. Les mathématiques deviennent donc un outil, et non plus une vérité absolue. « Nous sommes maintenant en 2006, 100 ans exactement après la naissance de Gödel (28 avril 1906), et nous ignorons encore l'importance de son résultat d'incomplétude. L'incomplétude des mathématiques doit-elle nous inciter à les pratiquer différemment ? L'avenir nous le dira » (Chaitin, 2006, p. 70-76).
3.1.3.2.2. La problématique
La problématique est « l'intermédiaire entre la logique formelle et la recherche concernant le contenu » (Grawitz, 2001, p. 4). « Elle répond à un besoin de cohérence logique, met en œuvre un ensemble de problèmes qui orientent la recherche et un corps de concepts qui, directement ou indirectement, débouchent sur des hypothèses rendant compte d'un contenu riche de conflits » (Grawitz, 2001, p. 4). Ce qui signifie que « forme et contenu ne peuvent être totalement séparés et la logique, même formelle, garde malgré tout une signification concrète dont la limite imprécise laisse entier le problème essentiel : comment unir la forme et le contenu, passer de l'être passant à l'être existant ? » (Grawitz, 2001, p. 4). C'est le dualisme kantien entre la forme et son contenu ; la pensée et l'objet à connaître (la « chose en soi »).
3.1.3.2.3. Les raisonnements
Le raisonnement déductif est avant tout une démonstration. Le raisonnement déductif part du champ phénoménal pour dégager un champ théorique. Les faits construisent leur propre théorie. Des prémisses supposées entraînent des conséquences déduites qui sont des certitudes comme la mathématique. C'est la conception aristotélicienne.
Le raisonnement inductif recherche la généralisation. Le raisonnement inductif part du champ théorique pour expliquer le champ phénoménal. Le fait observé entre dans un concept existant. Le processus de généralisation est nécessairement une abstraction. Le meilleur exemple est le syllogisme qui comprend trois propositions : la majeure, la mineure et la conclusion. Une erreur amène une contradiction. Il peut être envisagé par trois approches, décrites par Bernard Lepetit (in Revel, 1996, p. 71-94). La première approche est d'utiliser un concept existant pour passer d'un objet singulier à une généralité. La seconde technique, si le concept est imparfait ou inexistant, est d'effectuer un échantillonnage statistique, et le généraliser à toute une population mère. C'est un raisonnement inductif, très largement répandu dans les différentes sciences. La troisième possibilité est d'utiliser la ressemblance entre plusieurs faits, et les généraliser. C'est un raisonnement analogique, peu utilisé à l'heure actuelle parce qu'il a été discrédité par la modernité de Galileo Galilei et de René Descartes.
Le débat entre raisonnement déductif et raisonnement inductif est loin d'être tranché. À la rigueur de la déduction s'oppose la richesse de l'induction. Toutefois, ils peuvent se décliner en d'autres types de raisonnement comme le raisonnement par l'absurde ou l'abduction. Le raisonnement par l'absurde consiste à démontrer un théorème en montrant que des conséquences contradictoires résultent de l'hypothèse contraire. Il essaye de prouver qu'une hypothèse est fausse parce qu'elle ne peut pas entrer dans un champ théorique existant, ni même en établir un.
Le raisonnement dit de l'abduction a été élaboré par Charles Peirce (1839-1914). Il consiste à « remonter » de l'effet à la cause, c'est-à-dire reconstruire les étapes d'un processus à partir du résultat actuel, se distinguant de la déduction qui emprunte un chemin inverse (de la cause vers l'effet).
3.1.3.3. Les concepts.
« Toute science utilise des mots et des concepts » (Aron, 1969, p. 116). Le but de toute science est de construire un objet scientifique, c'est-à-dire un concept, une matière d'étude universelle servant de généralisation. « Le mot ne remplit entièrement sa fonction que s'il a une signification exacte, autrement dit, s'il correspond à un concept » (Aron, 1969, p. 116-117). Un concept est donc une représentation mentale générale et abstraite d'un objet ou d'une idée. Il définit les caractères spécifiques d'un projet, d'un produit, par rapport à l'objectif ciblé. Toutefois, certains concepts sont également sources d'échange entre les différentes disciplines.
Il faut préciser qu'un concept n'est pas le phénomène lui-même. C'est une abstraction, une pensée, un moyen de connaissance. Le concept est, en réalité, double. Il représente une activité pratique, sensible, le contact avec le monde sous la forme des êtres singuliers. Progressivement, son contenu devient une abstraction universelle. Le concept formé va au-delà de l'immédiat sensible, de l'apparence, du phénomène, dans un degré supérieur d'objectivité. « La logique du concept est une logique de l'essence » (Lefebvre, in Grawitz, 2001, p. 18). C'est un outil qui permet de comprendre.
Le concept est plus ou moins étendu, plus ou moins compréhensif. Si l'étendue est grande, le concept est peu compréhensif. Les concepts se créent, s'enrichissent et disparaissent sans que leurs contours obéissent à une délimitation rigoureuse. On reconnaît au concept une valeur de généralité. Sur l'élaboration des concepts, empiristes et rationalistes s'affrontent. Ainsi, Jean-Paul Delahaye (1994) distingue trois catégories de concept. Le concept est dit effectif lorsqu'il définit son contenu par un moyen sans ambiguïté. Le concept constructif se précise au fur et à mesure que les travaux avancent : il est impossible de le définir sans ambiguïté. Le concept prospectif est un discours où rien n'est explicite. C'est un mot issu de la langue courante sans connotation scientifique.
Cependant, il faut distinguer les concepts et les termes correspondants, c'est-à-dire les expressions verbales ou symboliques qui représentent ces concepts. Pour mentionner des termes particuliers et des choses particulières de n'importe quel autre genre, on a besoin de noms ou de désignations. En accord avec une convention classique de la logique et de la philosophie analytique, on forme un nom ou une désignation d'un terme en le mettant entre des guillemets anglais.
D'après Carl Hempel (1996), il existe deux types de définition dans un concept :la définition nominale et la définition réelle. La définition nominale utilise un mot ou une phrase (definiens) comme substitut d'une autre (definiendum). Autrement dit, le concept, dans ce cas, a la signification qui lui est donnée arbitrairement. Le concept ne prétend à d'autre vérité que la conformité à sa propre définition : il n'ajoute rien à nos connaissances, mais peut, sur le plan méthodologique, aider à les accroître. Le risque de cette définition est que celle-ci peut être considérée comme réelle par ceux qui l'emploient. Ladéfinition réelle désigne l'objet par ses caractéristiques essentielles : elle suppose donc une vérité. Elle établit une équivalence entre le défini et la définition. Elle dépasse le plan du langage pour atteindre celui de la connaissance. Il faut remarquer que l'on juge les définitions nominales d'après leur utilité, tandis que les définitions réelles sont jugées d'après leur vérité.
Toutefois, il existe également des définitions dites opératoires. Le concept opératoire de Karl Popper (1902-1994) est la mesure même qui mesure la mesure à mesurer. L'idée centrale de l'opérationnalisme est que la signification de chaque terme scientifique doit pouvoir être déterminée en spécifiant une opération de vérification bien définie qui lui fournit un critère d'application. Elles exigent une cohérence des critères opératoires, mais cela encourage la prolifération de concepts très proches et la multiplication de définitions pour un même terme. Les étalons opératoires peuvent donc avoir un usage dangereux. Il ne faut donc pas isoler une hypothèse sous prétexte qu'elle n'a pas été définie, ce qui signifie que la définition opératoire est de moins en moins utilisée. En effet, il faut admettre que dans ce concept opératoire, Karl Popper exprime clairement sa vision libérale du monde : tout devant être utile et utilisable ou disparaître, vision qui peut être dangereuse. Comment peut-on évaluer, par anticipation, « opérationnabilité » d'un concept ?
Enfin, il faut donner les trois éléments de définition d'un concept scientifique.
Il y a habituellement le choix entre plusieurs critères d'application pour un terme et ceux-ci reposent sur des ensembles différents d'opérations.
Pour comprendre la signification d'un terme scientifique et l'utiliser à bon escient, on doit connaître le rôle qu'il joue dans un système et ce qu'indiquent les principes théoriques dans lesquels il figure et qui le relient à d'autres termes théoriques.
Un terme scientifique ne peut pas être considéré comme « synonyme » d'un ensemble d'opérations, au sens où sa signification serait complètement déterminée par elles.
3.1.3.4. Les théories
Une théorie a pour but d'identifier les causes et les effets entre les faits objectivés. La théorie englobe principes et concepts, ainsi que les modèles. Celle-ci est liée à un courant de pensée appartenant à l'époque qui l'a produite, ce qui signifie qu'une théorie est « mortelle ». On estime qu'elle a une espérance de vie moyenne limitée à une cinquantaine d'années. Il faut confronter le point de vue des rationalistes et des empiristes sur les théories. « Pour un rationaliste, le critère de la vérité ne dépend pas de nos sens : il est intellectuel. » (Grawitz, 2001, p. 16). Les théories sont des constructions logiques, des schémas conceptuels. C'est la conception platonicienne de la théorie. A contrario, « l'empiriste affirme que l'origine de la connaissance se trouve dans l'expérience. Il croit en la valeur de l'observation et en celle de la sensation » (Grawitz, 2001, p. 16). C'est la conception aristotélicienne de la théorie.
Une théorie a trois objectifs :
décrire et montrer ;
expliquer et comprendre ;
prédire et prévoir.
Pour satisfaire à ces objectifs, les théories utilisent les lois qui sont des relations formalisées et mathématiques. Elles transcrivent un fait régulier et récurrent. Par exemple, les lois de la physique relèvent du laboratoire. Les faits observés sont de plus en plus soumis à des expériences éloignées de la réalité. La loi est une propriété de la nature. Cependant, la nature est complexe et la loi est simple. Autrement dit, la loi n'est qu'un moyen, une régularité statistique. Par cette relation répétable le scientifique cherche à construire des objets scientifiques. Il existe deux types de lois : la loi stricte et la loi de l'évolution. « Les entités et les processus fondamentaux postulés par une théorie et les lois supposées les régir doivent être définis avec toute la clarté et la précision souhaitables ; faute de quoi, la théorie ne peut remplir son but scientifique » (Hempel, 1996, p. 110-111). Le problème est qu'il existe des théories qui ne sont pas testables comme la plupart des théories de l'évolution que ce soit celle de Charles Darwin ou celle de Laurent Nottale. Cependant, certaines sont testables de façon probabiliste comme les méthodes Monte Carlo. Quoi qu'il en soit, toute théorie est mortelle. Il suffit de montrer qu'il existe un contre exemple à la loi dégagée pour invalider ou mettre le doute sur la théorie.
Pour conclure, il faut préciser qu'il serait excessif d'exiger qu'une théorie corresponde à la réalité : d'une part, parce que la réalité est inaccessible par nos sens et d'autre part, parce que ce n'est pas l'objectif de la théorie. Elle cherche plutôt à offrir quelques clefs permettant de comprendre le monde dans lequel nous vivons. Autrement dit, la critique classique de l'analyse spatiale, au sein de la géographie, n'a aucun sens. En effet, nombreux sont ceux qui s'indignent sur le fait que l'analyse spatiale s'éloigne de la « réalité », mais cela est parfaitement normale et légitime par rapport son projet.
3.1.3.5. Les modèles
Un modèle consiste en la représentation formelle d'idées ou de connaissances, relatives à un phénomène. Le modèle est beaucoup moins vaste qu'une théorie. Il a justement une vision opérationnelle de la recherche. Tout modèle est un compromis entre une simplicité incomplète et un réalisme reflétant la complexité de la réalité. Le modèle implique la mise en forme de relations entre certains facteurs, c'est-à-dire la sélection de variables et leur mise en place respective. Le modèle est souvent visuel : c'est un assemblage topologique d'éléments.
En géographie, l'utilisation de modèles est de plus en plus fréquente car ils sont un bon compromis entre le champ phénoménal et le champ théorique. Peter Haggett (1973) souligne que le modèle est économique car il permet de transmettre ce qu'il y a de général dans l'information sous une forme très condensée. Le modèle est stimulant, car l'application permet d'en voir les lacunes qui conduisent à de nouvelles recherches, à de nouveaux modèles.
Le modèle scientifique est extrêmement rare car il est totalement décrit, explicité, vérifié, valable de tout temps et en tout lieu. La plupart des modèles sont donc à la fois des outils et des catégories intermédiaires soumis à une évolution de pensée constante. « Comprendre ce qui se passe autour de nous revient en réalité à construire des modèles et à les confronter à nos observations » (Prigogine, Nicolis, 1992, p. 279).
3.1.4. Le champ ontologique
3.1.4.1. Être et objets
Le champ ontologique est une réflexion sur le statut de la réalité. On y réfléchit sur la vérité contenue dans les sciences. Il possède deux entités : l'être et les objets construits. L'être existe de tout temps et en tout lieu. L'objet construit n'existe que par la théorie qui l'a élaboré.
3.1.4.2. Les paradigmes
Les paradigmes sont des « découvertes scientifiques universellement reconnues qui, pour un temps, fournissent à une communauté de chercheurs des problèmes types et des solutions » (Kuhn, 1983, p. 11). Les paradigmes de Thomas Kuhn sont vagues ! Il s'agit d'une acceptation souple et mal définie. En grec, paradigme signifie « exemple ». De plus, qu'est-ce qu'une communauté scientifique ? En vérité, c'est beaucoup de choses. Elle peut recouvrir l'ensemble de la communauté des chercheurs. Cela revient à dire qu'il existe des problèmes types et des solutions types qui mettent tous les chercheurs d'accord. Incontestablement, il s'agit ici d'un synonyme de « cadres doctrinaux » ; c'est dans ce sens que Marc Luyckx-Ghisi (2001) emploie le terme. Cependant, les paradigmes peuvent également, selon la définition de Thomas Kuhn, ne satisfaire qu'une communauté scientifique. Dans ce cas, le sens du terme paradigme devient flou. Est-ce un synonyme de projet disciplinaire ou de théorie ou de concept ? La meilleure réponse est, sans doute, une réponse balancée : « ça dépend du contexte ou de la phrase ». Pour Jacques Leca, le paradigme n'est pas une théorie, mais un ensemble de propositions partagées par un groupe de chercheurs, organisant la façon d'aborder un fait concret, de découper un certain nombre de questions à propos de tel objet, d'élaborer des méthodes d'établissement et d'évaluation des preuves, de formuler des généralisations découlant de ces preuves. Toutefois, le terme « paradigme » est très pratique pour désigner un ensemble de théories, de concepts et un projet disciplinaire puisqu'il désigne les découvertes scientifiquement reconnues pour un temps. Ainsi, un paradigme, au niveau d'une discipline ou d'une sous-discipline, est un agrégat cohérent de théories et de concepts, unis par un projet disciplinaire. Pour ne pas confondre les deux définitions, il faut appeler le paradigme, cadre doctrinal, métaparadigme, et on nommera l'autre paradigme tout simplement.
On observe au XXIe siècle que de nombreuses sciences attaquent de plus en plus les métaparadigmes. Autrement dit, le modèle cartésien, moderne, admis depuis des siècles, n'est plus universel. Certaines disciplines ouvrent de nouvelles possibilités. Pour bien comprendre cette évolution qui passe presque inaperçue en ce début du XXIe siècle, il faut entreprendre un rapide panorama de l'histoire des sciences de l'Antiquité à nos jours, le but étant de montrer l'apparition d'un nouveau métaparadigme.
3.2. Les cadres doctrinaux
Il existe de nombreux cadres doctrinaux (ou métaparadigme). Marc Luyckx-Ghisi (2001) complète la définition du paradigme en lui ajoutant une influence sociétale non négligeable. Il s'agit d'un cadre de pensée dans lequel se trouvent la société et la communauté scientifique. La doctrine scientifique pose la croyance scientifique. Il existe plusieurs doctrines scientifiques. En Occident, trois semblent avoir été mis en œuvre : le paradigme de la pré-modernité, le paradigme de la modernité et le paradigme de la « transmodernité » qui serait en cours de construction autour des sciences de la complexité.
3.2.1. Le paradigme pré-moderne
C'est celui qui va être mis en avant pendant 3000 ans (2500 a.-C. – 1600 p.-C.). L'homogénéité de cette période est contestable, ne serait-ce que par la division traditionnelle de l'Antiquité et du Moyen Age. Certes, le point de rupture n'est pas négligeable : le passage de sociétés polythéistes à des sociétés monothéistes demeure un grand changement dans la conception de la science. Toutefois, comme de nombreux historiens l'ont montré, le passage de l'Antiquité au Moyen Age s'accompagne d'une continuité de la philosophie antique qui s'est adaptée à la chrétienté ou encore à l'islam. Si on prend l'exemple de Platon, il fut interprété par saint Augustin. Aristote, quant à lui, a été interprété, entre autres, par saint Thomas d'Aquin. La coexistence des deux pensées ne fut pas pacifique. Il suffit de rappeler la querelle des Universaux, mais d'un point de vue philosophique et scientifique, on ne peut y voir une rupture nette. Les conceptions antiques demeurent dans les conceptions médiévales, et même celle du début de la Renaissance.
D'après Marc Luyckx-Ghisi, le paradigme pré-moderne aurait d'abord la particularité d'être vertical et autoritaire, patriarcal, intolérant car sa vérité est exclusive. La pré-modernité est opposée à la sécularisation. Cependant, le système symbolique présente l'énorme avantage d'être stable et poétique. Le monde de la magique domine. Le système est enchanté. Il n'existe qu'une seule science : la théologie. La pré-modernité a un sens du sacré évident et non discuté.
3.2.2. Le paradigme moderne et postmoderne
À partir du XVIIe siècle, on manifeste une attention particulière pour les méthodes et les démarches de la pensée, un déplacement d'intérêt de la métaphysique à la théorie de la connaissance. La science dite moderne est fondée sur le rejet de la cause formelle et de la cause finale. Les fondateurs en sont René Descartes et Galileo Galilei. Dans son Discours de la méthode (1637), René Descartes formalise les idées que reprendra Galileo Galilei. Il met en avant les causes efficientes. Autrement dit, il s'agit de rechercher l'origine de l'existence d'un objet : sa raison d'être. Il organise tout travail de recherche autour d'une méthodologie articulée par quatre préceptes constituant sa méthode, devenus classiques aujourd'hui.
René Descartes (1596-1650) est-il un des pères de la modernité ? Le débat reste ouvert. Quoi qu'il en soit, sa méthode est au cœur de la science moderne. Il insiste sur la valeur des mathématiques non pour leur précision quantitatives, mais seulement pour la certitude et l'évidence de leur démarche. « Descartes inaugura un nouveau paradigme numérique, fondé cette fois sur ce qu'aujourd'hui nous appelons analyse, c'est-à-dire les nombres réels. La géométrie devint analytique, et points et entités géométriques furent réduits à des coordonnés et équations : par exemple, les droites à des équations de premier degré » (Odifreddi, 2004, p. 18). Il cherche à prouver la validité de la science. Comment concilier l'univers quantitatif et la perception qualitative ? Qui nous dit que nos représentations s'accordent avec les choses et que le monde est intelligible ? René Descartes pratique le raisonnement expérimental en adoptant un système de raisonnement hypothético-déductif. « Avant Descartes, le hasard seul, ou le génie, permettait de résoudre une question géométrique [(c'est la méthode d'invention)] ; après Descartes, on a pour arriver au résultat des règles infaillibles [(c'est la méthode de résolution)] ; pour être un géomètre il suffit d'être patient » (Poincaré, in Bachelard, 1934, p. 169-170). Il développe une vision mécaniste du monde. Enfin, il faut préciser que, pour lui, la raison s'accorde aux choses parce que toutes deux sont l'œuvre de Dieu. L'évidence est le critère de la vérité. La vérité est dégagée par le sensible. Autrement dit, la base de la science n'est pas expérimentale.
« Le premier était de ne recevoir jamais aucune chose pour vraie que je ne la connusse évidemment être telle, c'est-à-dire d'éviter soigneusement la précipitation et la prévention et ne comprendre rien de plus en mes jugements que ce qui se présenterait si clairement et si distinctement à mon esprit que je n'eusse aucune occasion de le mettre en doute.
« Le second, de diviser chacune des difficultés que j'examinerais en autant de parcelles qu'il se pourrait et qu'il serait requis pour les résoudre.
« Le troisième, de conduire par ordre mes pensées, en commençant par les objets les plus simples et les plus aisés à connaître, pour monter peu à peu comme par degrés jusqu'à la connaissance des plus composés : en supposant même de l'ordre entre ceux qui ne se précèdent point naturellement les uns les autres.
« Et le dernier, de faire partout des dénombrements si entiers et des revues si générales que je fusse assuré de ne rien omettre »(Descartes, éd. 1999, p. 27).
Le premier précepte révèle le premier principe de la modernité proposée par René Descartes : l'évidence. Cela consiste à prétendre qu'un fait peut s'expliquer simplement, d'une manière évidente. Autrement dit, la complexité des êtres et des objets n'est qu'apparente. « Descartes a fondé la méthode d'analyse scientifique en posant que, pour résoudre un problème complexe, il suffit de le séparer en parties plus simples, de décrire ces parties plus simples, puis de les réintégrer pour obtenir une compréhension du tout » (Nottale, 1998, p. 31-32). Ce principe nie également les causes finales et formelles puisqu'il veut « éviter soigneusement la précipitation et la prévention ». C'est donc la victoire de la pensée platonicienne. Cependant, il faut relativiser cette négation de la cause formelle. En effet, la forme existe toujours, mais elle est réduite à une perception phénoménologique. Parfois, elle peut être idéalisée avec un formalisme mathématique. Cela va des formes euclidiennes banales (le cercle, le carré, le triangle) jusqu'à des formes particulières comme les formes fractales.
Le second précepte est le réductionnisme. Il s'agit de partir de l'idée que la complexité du monde n'est qu'apparente, et de le découper en petits problèmes, de manière à aboutir à une chaîne qui mettra en lumière les évidences du premier précepte. Aujourd'hui, le réductionnisme cartésien fait l'objet d'une vigoureuse controverse. Le problème principal du réductionnisme est que « les méthodologies réductionnistes marchent tant que les éléments présentent une individualité bien définie, tant qu'ils présentent des caractères d'immuabilité bien marqués. Quand ils sont plus « flexibles » et qu'ils n'ont pas une individualité très nette, la décomposition du système en éléments ne se révèle plus efficace » (Thom, 1983, p. 85-86). Cependant, pour Laurent Nottale, « la méthode cartésienne a parfois été taxée de réductionnisme. C'est, à mon avis, un faux procès qui procède précisément d'une réduction de la pensée cartésienne. Peut être réductrice, effectivement, une application restreinte de cette méthode à un problème particulier. Mais il est remarquable qu'au cas où un tel blocage de la pensée survienne (ce qui arrive souvent en physique), l'appel au mode de pensée cartésien apporte souvent la solution au problème tout simplement parce qu'il s'agit en fait d'une méthode générale d'analyse des lois de la nature. Par l'exemple, l'idée que le tout soit la somme des parties (exemple d'idées « réductionniste ») ne fait pas explicitement partie du point de vue cartésien. Il s'agit d'analyser le système considéré pour y découvrir des parties plus simples dans leur description, mais l'identification de ces parties peut parfaitement être plus complexe qu'un simple découpage, et la reconstruction du tout plus élaborée qu'un simple collage… » (1998, p. 32). L'argumentation de Laurent Nottale mérite d'êtreretenue mais le propos cartésien a été déformé au cours des siècles, notamment par le positivisme, pour devenir réductionniste. Il l'est toujours aujourd'hui.
Enfin, il faut présenter la pensée de Gaston Bachelard (1934). « La méthode cartésienne est réductive, elle n'est point inductive. Une telle réduction fausse l'analyse et entrave le développement extensif de la pensée objective. Or il n'y a pas de pensée objective, pas d'objectivation, sans cette extension. […] La méthode cartésienne qui réussit si bien à expliquer le Monde, n'arrive pas à compliquer l'expérience, ce qui est la vraie fonction de la recherche objective » (Bachelard, 1934, p. 142). Gaston Bachelard critique René Descartes pour sa recherche des natures simples et absolues. Il admet que dans certain cas la méthode dite cartésienne est suffisante. « Pour les savants du XIXe siècle aussi bien que pour Descartes, les bases rationnelles du mécanisme étaient inébranlables » (Bachelard, 1934, p. 186). Cependant, il note un certain abus dans les explications scientifiques de cette méthode.
Le troisième précepte est la mise en avant de la causalité efficiente. Celle-ci est fondée sur la continuité de la chaîne produite par le processus. Elle ne peut donc pas être lacunaire. Elle est pensée sur le modèle de la linéarité, puisqu'une petite cause génère un petit effet et qu'une grande cause produira un grand effet. C'est le fameux rationalisme d'Aristote. Il suffit donc de remonter la chaîne des évidences pour expliquer la complexité du monde. En revanche, il ne faut pas confondre causalité et déterminisme. Une causalité peut être qualitative et/ou quantitative alors que le déterminisme ne concerne que le quantitatif. Ainsi lorsque les humanités prétendent qu'elles ne sont pas déterministes, elles n'expriment qu'une tautologie puisque la plupart d'entre elles ne sont que qualitatives2. Cependant, aujourd'hui, dans un système complexe, la causalité change de statut : elle devient indéterminable. On ne peut jamais prouver qu'un phénomène a été provoqué par telle ou telle cause, ou plus exactement la cause ultime qui sera amplifiée par la non linéarité du système ne peut être identifiée. Comment identifier la vibration d'un atome qui déclenche un tremblement de terre ou une avalanche ?
Le quatrième précepte correspond au principe d'exhaustivité. Il est basé sur le fait que l'information scientifique est nécessairement infinie, et qu'il faut la recenser le plus précisément possible. La conséquence de ce principe est qu'il y a toujours quelque chose à découvrir. Cependant, il semblerait que les sciences aient aujourd'hui atteint une limite. En effet, le rythme des découvertes majeures en physique, par exemple, tant dans le champ phénoménal et dans le champ théorique, a fortement ralenti depuis le milieu du XIXe siècle. De plus, nombreux sont les scientifiques qui croient que ce principe est un mythe. C'est sans doute pour cela qu'ils ont mis l'accent sur le second principe de René Descartes. Enfin, l'exhaustivité de la mesure a provoqué une « inflation » de l'information.
Galileo Galilei, père de la modernité, a associé la chute libre d'un corps à la variable temps. Cette équation a permis une mise en avant de la cause efficiente d'Aristote puisqu'elle dissocie pour la première fois dans l'histoire des sciences, temps et espace. La cause efficiente est également liée aux forces présentes dans l'univers. Les causes finales et formelles n'existent plus. Quant à la cause matérielle, elle est maintenue, parce que la nier serait nier l'existence des objets d'étude, c'est-à-dire le fondement des sciences. Galileo Galilei éprouve la méthode de René Descartes en quelque sorte.
Cette construction scientifique s'est bâtie de concert, avec ce qu'il est commun d'appeler, la société moderne. La science y tient une place éminente. La modernité a développé ainsi son propre modèle social, qui est globalement toujours en place aujourd'hui. D'après Marc Luyckx-Ghisi (2001), il consiste à partager la vie des individus en deux : une vie appartenant au domaine privé, une autre appartenant au domaine public. La vie publique est un système social hiérarchique dont on peut considérer qu'il est dominé par les tenants du pouvoir scientifique tout autant que par les tenants du pouvoir politique, les élus. La vie privée est un autre monde où se meuvent d'autres dimensions de la vie sociale. C'est de ce côté qu'une partie des causes aristotéliciennes et des entités matérielles ou immatérielles comme la forme se retrouvent de facto. Dans le domaine public, au sommet de la pyramide se trouve la raison, il s'agit bien sûr d'une dimension en rapport étroit avec les causes efficientes. Ensuite, viennent ceux qui sont capables de décoder ces causes : d'abord les scientifiques, ensuite les politiciens qui appliquent les progrès dégagés par les scientifiques ; enfin, le reste de la société où l'homme est nettement supérieur à la femme. Dans une vision moderne, les causes finales et formelles relèvent donc de questions métaphysiques entrant dans le champ de la philosophie et de la littérature. Elles recouvrent des faits qui ne sont pas scientifiquement objectivables. Ce paradigme de la modernité offre une autre solution au problème philosophique de la liberté de l'homme puisque, désormais, il possède un espace de libertés : son domaine privé, et un espace de contraintes : le domaine public. Grâce à cela, on met en avant le progrès scientifique. Ainsi l'espace de contraintes devient utilitaire au libre-arbitre humain. Dans cette position, on comprend l'intérêt scientifique et philosophique de l'histoire. Elle permet d'être au cœur de la liberté humaine en formulant son propos de la manière suivante : hier, on en était là, aujourd'hui, on en est là, et demain, on en sera sûrement là. Cette liberté est fondée sur l'idée que l'homme est, par nature, bon, ce qui reste en soi à démontrer. Toutefois, la raison placée au sommet de la pyramide a posé problème. L'utilisation du terme renvoie à une vérité absolue qui, en soi, n'existe pas.
Ce schéma moderne rencontre aujourd'hui des difficultés. Pour les résoudre, l'astuce trouvée a été, dans le schéma postmoderne, de remplacer la raison par l'idée qu'il n'existait pas une vérité, ce qui pose d'autres problèmes. En effet, cela met sur un même pied d'égalité un astrophysicien avec un astrologue, par exemple… Par ailleurs, les progrès de la science et de la technologie produisent de plus en plus des inquiétudes plus ou moins raisonnables (OGM, réchauffement climatique, déchets nucléaires, etc.). La postmodernité est fondée sur un scepticisme. Toutefois, ce début d'évolution du paradigme de la modernité semble indiquer que la modernité entre en crise à la fin du XXe et se poursuit en ce début du XXIe siècle.
3.2.3. Le paradigme transmoderne
La vision de la recherche formulée par la modernité a été contestée par l'approche systémique mise en place depuis une cinquantaine d'années. Objectivement, le paradigme transmoderne n'existe pas. Ce n'est qu'une appellation pratique donnée par Marc Luyckx-Ghisi (2001). Personnellement, ce terme me semble plus approprier que « paradigme de la complexité ou du chaos » qui est plutôt réducteur, mais plus fréquent dans la littérature. Il a été, en quelque sorte, annoncé par Gaston Bachelard dans le chapitre 6 intitulé « l'épistémologie non cartésienne » du Nouvel esprit scientifique (1934). Cependant, la découverte de la complexité commence par l'élaboration de la théorie des systèmes dans les années 1950.
Un système est un ensemble cohérent d'éléments interdépendants et non hiérarchisés. La systémique est l'étude d'un rapport entre le système et son environnement, d'une organisation, d'une structure et de son fonctionnement, et d'une dynamique propre au système. Cette approche possède, comme l'approche cartésienne, quatre préceptes : la pertinence qui est le rapport entre l'objet d'étude et le chercheur, « qu'est-ce que cette étude va lui apporter ? », la globalité qui considère que le tout du système l'emporte sur la somme des éléments qui le composent, la téléologie qui cherche à établir le comportement du système : on considère le système comme un être vivant, et l'agrégativité qui essaye de représenter de manière simplifiée les éléments connus du système.
La systémique articule ces préceptes autour de deux notions fondamentales : l'interrelation et la totalité. Il s'agit d'avoir, en quelque sorte, une approche holistique du monde, c'est-à-dire l'art de la synthèse expliquant la globalité. Elle propose une méthode qui serait à l'opposé des préceptes de René Descartes. Il n'y a plus de réductionnisme, plus d'évidence, plus de causalité linéaire et continue et plus de recherche de l'exhaustivité des données (fig. 4).
Les préceptes de l'approche cartésienne | Les préceptes de l'approche systémique |
|---|---|
évidence | pertinence (par rapport au problème) |
réductionniste (priorité à l'analyse) | globaliste ou holiste |
causalité (raisonnement linéaire) | |
exhaustivité | agrégativité |
La systémique réintroduit le raisonnement analogique qui avait perdu de son importance avec l'approche cartésienne, puisqu'il est fondé sur la comparaison de différentes formes. Il est vrai que l'analogie peut prendre un aspect très simple et parfois erroné. Toutefois, avec le développement de la systémique, l'analogie peut s'avérer beaucoup plus complexe. Il y en a trois types : les métaphores, les isomorphismes et les modèles. Les métaphores sont des comparaisons entre différents éléments dont le processus de fabrication est identique. Les isomorphismes travaillent sur une analogie structurale. Les modèles sont des représentations abstraites de réalités concrètes. Ils représentent la forme la plus élaborée de l'analogie. À cela, il pourrait être ajouté l'homologie, l'identité des structures comme telles identifiée par des lois de décroissance ou de croissance exponentielle. Grâce au raisonnement analogique et homologique, on peut entreprendre des recherches interdisciplinaires, nécessaires aujourd'hui pour créer des ponts entre les différentes disciplines académiques, ce qui permettra d'élaborer une méthodologie générale pour traiter les objets d'étude appartenant à plusieurs disciplines.
La systémique propose une recherche opérationnelle c'est-à-dire qu'elle se veut finalisée. Elle se fait par étapes successives. La première étape consiste à définir le système et son environnement avec ses entrées et ses sorties. La seconde étape doit montrer ou expliquer l'organisation du système. Cette étape est double : il s'agit de rechercher un état, c'est-à-dire une structure, et un processus, c'est-à-dire un ensemble de fonctions. Pour les établir, il faut chercher la frontière (ou la limite) entre le système et son environnement, puis définir les éléments qui composent le système, ensuite étudier les connexions entre les différents éléments, c'est-à-dire les réseaux, et enfin, trouver ce qui peut servir de réservoir au système. Une fois ce squelette mis en place, il faut chercher les flux, le ou les centres de décisions, les boucles de rétroaction et les délais de réponse. L'établissement de la structure et du processus conduit à définir des lois qui commandent le système, et à comprendre les relations internes et externes du système. À l'intérieur, l'état, c'est-à-dire la structure, correspond à un organigramme qui établit ce que l'on appelle les modules (ou sous-systèmes) en même temps que leur niveau (ou hiérarchie). L'état défini, il faut trouver le mécanisme de fonctionnement : le processus qui gère les différents éléments du système ainsi que les différentes relations entre les niveaux. Ce processus est un programme qui maintient la structure du système. Cependant, il faut remarquer qu'à l'extérieur du système, un certain degré de fermeture existe toujours. Il permet de maintenir l'identité propre du système considéré.
La structure et les fonctions du système comprises, on peut passer à la troisième étape qui consiste à rechercher la dynamique du système étudié. Il en existe essentiellement deux. Un état stationnaire correspond à un système qui s'adapte dans toutes les situations difficiles qui se présentent à lui. Lorsqu'on l'observe, il donne l'illusion d'être immobile, d'être en équilibre. Celui-ci est obtenu par une régulation qui s'appelle l'homéostasie. Elle repose sur la capacité d'un système à produire ce que l'on appelle de la variété, c'est-à-dire le nombre de configurations, ou d'états, que ce système peut revêtir. « L'un des problèmes cruciaux avec ces phénomènes de contrôle est la robustesse : jusqu'où un système peut-il résister à de petits chocs ? » (Gleick, 1991, p. 337 et p. 372). Toutefois, trop de variétés peut conduire à une crise de la structure et des fonctions du système, et engendrer la deuxième dynamique possible : celle de l'émergence. L'émergence est une « apparition inattendue et soudaine (dans une série d'événement ou d'idées) » (Mayet, 2005, p. 5). Elle se produit lorsque le système ne peut plus être plus régulé. Deux cas sont possibles : soit le système redéfinit brusquement sa structure et ses fonctions, soit il est englobé dans un autre système, devenant ainsi un sous-système. L'émergence peut être soit spontanée, c'est-à-dire à partir de rien, soit évolutive, c'est-à-dire à partir d'une accumulation des tensions menant à une agrégation. Cependant, « l'émergence est considérée comme importante, mais sans qu'on sache souvent ce qu'elle est ! » (Sober, 2005, p. 10-13). Quoi qu'il en soit, l'émergence conduit à l'apparition d'un nouveau système qui n'a plus rien à voir avec l'ancien. L'émergence rappelle que le réel n'est pas homogène. Le réductionnisme pose la règle d'addition : le tout est égal à la somme des parties, tandis que l'émergentisme pose la règle d'interaction : le tout est supérieur à la somme des parties.
Les étapes précédentes conduisent à observer le système, ce qui a permis de le décrire. La quatrième étape consiste à vérifier, par l'intermédiaire d'une méthode pertinente, que la théorie obtenue par la description correspond à la situation pratique. Cette étape est le cœur de la recherche dite opérationnelle. Elle consiste à lier les différents éléments (les faits) entre eux, puis à faire intervenir dans ces différentes liaisons, le hasard, et enfin à expliquer la concurrence entre les éléments. Pour étudier correctement un système, il faut faire au minimum trois études : une étude combinatoire, une étude sur les variables aléatoires et une étude sur la concurrence. L'étude combinatoire travaille sur les invariants du système qui sont les éléments stables du système, ceux qui sont considérés comme fixes, non susceptibles de transformation. On étudie ces invariants par l'intermédiaire de deux techniques qui permettent d'associer les différents invariants : soit il s'agit d'un algorithme, c'est-à-dire une prescription détaillée des opérations à réaliser pour obtenir avec certitude la solution du problème posé, soit il s'agit d'un programme linéaire, c'est-à-dire la détermination des valeurs de variables ou d'activités en présence de contraintes relatives aux ressources disponibles et en vue d'obtenir le résultat optimum. Le choix aléatoire travaille sur les variables du système. Les variables sont des éléments du système dont les changements peuvent provenir soit d'événements aléatoires externes au système, soit de décisions du modélisateur qui est le véritable meneur de jeu. Cette analyse est menée par l'intermédiaire des probabilités, des analyses factorielles… Enfin, l'étude de la concurrence nécessite une connaissance de la théorie des jeux (Guerrien, 1995 ; Giraud, 2000) et de son application. Elle étudie le comportement des individus rationnels en interaction, et les conséquences de leurs choix, c'est-à-dire les contraintes exercées sur le système. Les contraintes sont internes ou externes au système. Elles limitent sa capacité d'adaptation ou de réaction à telle ou telle situation.
La cinquième étape consiste à présenter les résultats sous la forme d'une représentation graphique et à modéliser le système. La représentation graphique est soit un diagramme, soit une carte soit un réseau. La modélisation est le processus d'action qui conduit à la construction d'un modèle. Le terme de modèle s'applique à toute représentation ou transcription abstraite d'une réalité concrète. Cette représentation doit être assez simplifiée pour être intelligible, mais suffisamment fidèle pour être utile et fiable. Cette modélisation est difficile à réaliser. La plupart des modèles formulés sont faux. Il faut sans arrêt les retravailler pour atteindre quelque chose qui tend vers une juste image de la réalité. Cependant, il faut insister sur le fait que le modèle n'est qu'un résultat. Seul le processus de modélisation a un intérêt scientifique et méthodologique. Cette modélisation a pour but de pouvoir faire des simulations qui vont permettre d'établir une éventuelle prospective. Selon Daniel Durand (2002), il en existe quatre types : le modèle cognitif, le modèle décisionnel, le modèle normatif et le modèle prévisionnel. Le modèle cognitif doit donner une représentation simplifiée d'un système réel en ne retenant que les éléments et les interactions les plus significatifs du système. Le modèle décisionnel doit fournir au décideur des schémas qui lui permettent de prendre rapidement une décision en présence soit d'une information trop abondante, c'est-à-dire difficile à maîtriser, soit au contraire d'une information lacunaire ou incertaine. Le modèle normatif est une forme particulière du modèle décisionnel qui est particulièrement contraignante. Le modèle prévisionnel doit permettre de déduire le comportement futur d'un système à partir de la connaissance de l'état présent et passé de ce système. Cependant la nature d'un modèle est classable en quatre niveaux de compréhension : la maquette, le schéma, le modèle cybernétique et le modèle numérique. La maquette est un objet représentant à une échelle réduite l'objet mécanique ou le bâtiment que l'on veut construire ou étudier. Cette maquette peut être soumise à des tests, des mesures qui permettront d'améliorer les performances de l'objet ou du projet. Le schéma représente l'objet ou le système, existant ou à créer, de façon plus ou moins détaillée. Les schémas ou les dessins sont complétés par un code qui permet de les interpréter. Le modèle cybernétique permet d'étudier ou de prévoir les conditions de régulation d'un système. Le modèle numérique est lié au développement de l'informatique. Le modèle, quelle que soit la discipline qui l'a produit, s'inscrit dans un langage qui permet de le comprendre. Selon Daniel Durand (2002), ce langage se joue à trois niveaux : un langage graphique, qui fait appel à des notions de sémiologie, un langage mathématique, qui permet d'établir les lois d'ensemble du système, et un langage discursif, qui possède deux faiblesses : il est de nature linéaire alors que la plupart des systèmes ont des règles non linéaires, et il manque de rigueur ; il utilise un lexique flou, mais demeure indispensable pour trouver de nouvelles connaissances.
La systémique étudie la complexité du monde pour elle-même, mais comment différencier ce qui complexe de ce qui ne l'est pas ? D'après les principes de René Descartes, la complexité n'existe pas : elle n'est qu'apparente. Grâce à des chaînes linéaires et continues de causes et d'effets, on peut comprendre la complexité du monde par des expressions simplifiées de celui-ci. Depuis une trentaine d'années, on admet que le complexe a une réalité propre, irréductible.
Piergiorgio Odifreddi (2004) remarque que « les sciences et les mathématiques du XXe siècle ont en commun cette difficulté à expliquer leurs conquêtes en termes de concepts classiques. Mais difficultés ne signifie pas impossibilité. Ce sont souvent les abstractions superficielles et stériles qui sont plus difficiles à justifier tandis que celles qui sont profondes et fécondes puisent leurs racines dans des problèmes et des intuitions concrètes. En d'autres mots, la bonne abstraction n'est jamais une fin en soi, un art pour l'art, au contraire, elle est toujours une nécessité, un art pour l'homme » (2004, p. 11). Deux problèmes sont ici soulevés : (1) sur des centaines de milliers de théorèmes la plupart n'ont aucune importance et aucun intérêt ; (2) la fragmentation des sciences depuis le XVIIIe siècle a abouti a une hyperspécialisation au XXe siècle. En effet, « à force de nous spécialiser, nous devenons plus vulnérable,… et c'est la mort » (Ghost in the shell3). La complexité cherche à résoudre ces deux problèmes. « Les sciences de la complexité ne sont pas une école de pensée, une nouvelle idéologie scientiste : elles aspirent, au travers d'un ensemble de techniques et de principes, à proposer une description aussi fidèle que possible des phénomènes que la nature nous donne à voir » (Benkirane, 2002, p. 8). Deux disciplines ont contribué à la compréhension de la complexité : la physique du non équilibre et la théorie moderne des systèmes dynamiques dans lesquelles la prédominance de l'instabilité est la règle. « En bref, cela signifie qu'une petite modification des conditions initiales peut conduire à d'énormes amplifications » (Prigogine, Nicolis, 1992, p. 4).
La pensée transmoderne développée par Marc Luyckx-Ghisi (2001) essaye de lutter contre une vision classique de la science. La science n'est pas une accumulation de connaissances dont le vague souvenir est relancé au nom d'une quelconque expertise. Elle met en avant, entre autre, ce que l'on appelle l'ago-antagonisme (Bernard-Weil, 1988). Deux objets contraires s'opposent en même temps qu'ils se complètent, puisque chacun sert de référentiel à l'autre. Le rapport entre les individus obéirait à un abandon partiel de soi : l'individu est libre de faire ce qu'il veut, mais sous contrainte de son environnement, sinon celui-ci pourrait un jour se retourner contre lui, ce qui signifie qu'un individu possède des « degrés de libertés » en fonction du système social dans lequel il se meut. Le système sociétal devient donc une entité supérieure à la stricte somme des individus qui le composent.
La vérité est une perfection : on tend toujours vers elle, sans jamais l'atteindre. Pour arriver à l'approcher, il faut nécessairement avoir une démarche transdisciplinaire et construire un objet scientifique faisant appel à plusieurs disciplines. Ce nouveau cadre hypothétique de la modernité passe, en outre, par des processus non linéaires, des bifurcations, des horizons de prévisibilité, etc.
Comment étudier cette complexité, si elle existe réellement ? La méthode consiste, comme on l'a vu, à déconstruire les systèmes et à les étudier par l'intermédiaire de la recherche opérationnelle. Cependant, il existe également de nombreuses méthodes appelées « théories du chaos » par James Gleick (1991) parmi lesquelles on trouve la géométrie fractale.
3.3. Complexité, chaos et fractales
La complexité est un terme générique qui englobe toute science (ou tout sujet) dont la connaissance est liée à une notion d'échelle et/ou à la morphogenèse. Le chaos est déjà plus restrictif. Il étudie les systèmes déterministes non linéaires à comportement complexe. Quant aux fractales, elles constituent une foule d'objets géométriques, et purement géométriques qui ont la propriété d'être dépendant d'échelle. Le cas le plus simple est l'invariance d'échelle : de près comme de loin, l'observateur verra la même forme.
3.3.1. La complexité
Complexe « se dit de ce qui contient plusieurs parties ou plusieurs éléments combinés d'une manière qui n'est pas immédiatement claire pour l'esprit ». En effet, « la complexité d'un système se mesure par l'importance de l'intelligence qu'il faut mettre en face pour le comprendre et non par l'importance du temps nécessaire à le décrire » (Martin, 2004b, p. 26). Le mot vient du latin complexus qui signifie « tissé ensemble ». La complexité accepte comme postulat celui de la systémique : « le tout est plus que la somme des parties ». Toutefois, il faut préciser qu'il « existe pléthore de définitions [de la complexité]. Certaines s'appuient sur les notions d'information, d'entropie (le niveau de désordre d'un système), de chaos ou de hasard. Toutes, à des degrés divers, expriment une relation entre le tout et les parties d'un système, plus exactement le fait que la connaissance des parties ne suffit pas à expliquer le fonctionnement du tout » (Benkirane, 2002, p. 9).
Il faut faire attention. Le terme « complexité » doit être opposé à celui de « compliqué ». En effet, à la question, un système compliqué est-il complexe ? La réponse est non. Le compliqué est réductible par la méthode cartésienne, tandis que le complexe ne l'est pas. « Dans la mesure où la complexité se différencie de la complication et dans la mesure où les phénomènes non complexes donc linéaires, etc. s'avèrent, tant dans la nature que dans la société, rares, tout change. Il apparaît ainsi que ce qu'il faudra maintenant appeler le « vieux paradigme moderne » n'est pas suffisant pour comprendre, pour se représenter et donc pour vivre dans le monde, ce qui est fondamental » (b, t. 1, 2004, p. 22).
Le père de la complexité est Andrei Kolmogorov. Il a formulé ce que l'on appelle la théorie algorithmique de l'information (ou théorie de la complexité). Pour lui, le monde serait un ensemble de programmes mis en place en fonction de la taille de l'objet étudié. Plus un objet est « long », moins il est probable. Un système complexe ne peut se résumer en un algorithme court, tant la richesse des informations est importante. Ce genre de système présente une organisation qui n'est ni strictement définie, ni aléatoire, et produit des effets non linéaires dont l'expression est l'émergence de propriétés nouvelles.
« Pour la plupart d'entre nous, les phénomènes qui entrent dans les ouvrages de physique traditionnelle comme la chute d'un objet sous l'action de la pesanteur ou le mouvement du pendule, sont fondamentalement « simple ». À l'opposé, nous pourrions affirmer que notre système économique, notre langage, le cerveau des mammifères ou même la plus infime des bactéries sont des « systèmes complexes » (Prigogine, Nicolis, 1992, p. 9 et 11). Ce qui signifie qu'il « paraît plus naturel, moins ambigu, de parler de comportement complexe plutôt que de systèmes complexes » (Prigogine, Nicolis, 1992, p. 11).
Pour résumer, la complexité regroupe trois situations : le système possède beaucoup de degrés de liberté et a des équations dont on ne possède pas la solution ; le résultat, apparemment simple, adopte un comportement compliqué rendant une prospective impossible ; le système a un très grand nombre de variables et un comportement aléatoire. « Il existe en fait deux « styles » de complexité. L'une est la complexité de ce qui est aléatoire et elle est complexité parce que rien ne la résume. Elle n'est pas simple à concevoir contrairement à ce que nous pourrions initialement penser. Par exemple dessiner une distribution aléatoire de points est quelque chose de délicat. Mais inversement voir une structure dans une distribution aléatoire de point est possible. L'autre style est une « complexité » liée à une organisation. C'est la complexité qui rejoint le sens vernaculaire du mot de façon plus directe. Cette complexité correspond à ce qui est organisé, fortement structuré, riche en informations plus ou moins cachées, mais en informations organisées. Il faut essayer d'en rendre compte […] » (Martin, t. 1, 2004b, p. 27).
Enfin, ces sciences de la complexité fondent la réflexion de Marc Luyckx-Ghisi (2001) sur les conséquences que celles-ci auront sur la société. Il qualifie sa pensée de transmoderne. « Ce n'est pas tant que ces sciences de la complexité soient nouvelles ; ce qu'il faut voir ici, c'est la migration d'idées, auparavant en marge des courants principaux de la science, vers le cœur de l'activité scientifique » (Benkirane, 2002, p. 10-11). La complexité défend l'idée d'être « en bordure » avec les notions de « seuil critique » et de « frontière entre chaos et ordre ». Il s'agit d'assimiler le fait qu'un rien peut transformer complètement un système, ou plus généralement la « face du monde ».
« Qu'est-ce qu'un système complexe ? Il n'existe pas de définition mathématique universellement acceptée mais l'idée générale est qu'on ne devrait pas pouvoir décrire de manière concise le comportement d'un tel système, même s'il possède des éléments d'organisations bien précis. Les systèmes complexes ne sont ni ordonnés ni aléatoires, mais ils combinent de façon frappante bien qu'insaisissable des éléments des deux comportements » (Stewart, 1998, p. 550). « Il existe beaucoup de sortes de systèmes complexes. La complexité peut être purement spatiale – le système fait apparaître des formes compliquées, mais les formes n'évoluent pas dans le temps. […] La complexité peut être purement temporelle – la structure spatiale est simple à tout instant, mais elle évolue au cours du temps de façon complexe. […] Le système peut être complexe à la fois dans l'espace et dans le temps […]. Un système complexe peut être adaptatif, répondant à des influences extérieures, ou même aux résultats de son propre comportement, et « apprenant » d'eux – modifiant lui-même sa réponse » (Stewart, 1998, p. 530-531). À la différence de la pensée traditionnelle, pour la complexité, « le cœur de la discussion n'est pas tant ce qu'est réellement l'univers, mais comment les êtres humains peuvent l'appréhender. La vision traditionnelle de l'explication scientifique est relativement simples : l'explication d'un quelconque phénomène est la déduction de ce phénomène à partir de lois de la nature » (Stewart, 1998, p. 554).
Le monde sera une somme d'objets, de configurations spatiales dont le programme qui les a élaborées serait court. Plus le programme est court, plus on a de chances de le rencontrer. Cependant, Jean-Paul Delahaye (1994) rappelle constamment que la complexité du monde actuel n'exclut pas une origine simple.
Une énumération des problèmes me semble plus parlante qu'une description longue et fastueuse.
Le problème du changement de niveau d'intégration (ou l'émergence) :
avec le phénomène de réorganisation ;
avec le phénomène de simplification ;
Le problème de l'indétermination quantique ou fortuite :
avec le chaos déterministe :
une non linéarité ;
un retour de la sortie sur l'entrée ;
avec une sensibilité des conditions initiales ;
L'irréversibilité (c'est-à-dire la dépendance au passé) ;
La théorie des catastrophes et les mathématiques du chaos ;
La géométrie fractale ;
Les simulations informatiques (automates cellulaires, systèmes multi-agents).
Chaos et fractale entrent, en partie, dans le domaine mathématique de la topologie, fondée par Henri Poincaré. « Il s'agit des mathématiques de la continuité. La continuité est l'étude des changements réguliers, progressifs, la science du non brisé. Les discontinuités sont soudaines, dramatiques : des endroits où un minuscule changement au niveau de la cause produit un énorme changement au niveau de l'effet » (Stewart, 1998, p. 97). « La topologie est une sorte de géométrie, mais une géométrie où les longueurs, les angles, les surfaces, les formes sont infiniment transformables. […] Toutes [les] formes géométriques qu'on nous enseigne avec tant d'acharnement lorsque nous sommes enfants : pour un topologue, elles ne sont qu'une. La topologie n'étudie que les propriétés des formes continues réversibles » (Stewart, 1994, p. 97-98).
3.3.1.1 Définition de l'émergence
L'émergence est une « apparition inattendue et soudaine (dans une série d'événements ou d'idées) » (Mayet, 2005, p. 5). Il s'agit de la plus grande énigme des sciences de la complexité. Jean Petitot ajoute que l'émergence engendre de la simplicité en changeant de niveau (ou d'échelle plus exactement). L'émergence peut être soit spontanée c'est-à-dire à partir de rien, soit évolutive c'est-à-dire une accumulation des tensions menant à une agrégation. Cependant, « l'émergence est considérée comme importante, mais sans qu'on sache souvent ce qu'elle est ! » (Sober, 2005, p. 10-13).
L'émergence rappelle que le réel n'est pas homogène. « La notion d'émergence se comprend ainsi essentiellement comme un constat d'échec ou d'impuissance, provisoire ou définitif, du programme réductionniste en biologie ou en physique » (Mayet, 2005, p. 5). Le réductionnisme pose la règle d'addition : le tout est égal à la somme des parties, tandis que l'émergentisme, né en Angleterre au XIXe siècle, pose la règle d'interaction : le tout est supérieur à la somme des parties.
L'émergence va de pair avec le phénomène d'auto-organisation qui renvoie à une émergence ordonnée. « L'auto organisation est l'apparition spontanée d'une forme ou d'une structure qui ne résulte pas d'un programme codé comme un algorithme » (Sapoval, 1997, p. 166). L'un des objectifs de la complexité est de comprendre ces phénomènes d'auto-organisation.
La relativité d'échelle sera décrite plus en détail un peu plus loin dans la partie technique consacrée à la géométrie fractale. Du point de la compréhension du phénomène d'auto organisation et d'émergence, la relativité d'échelle va beaucoup plus loin que l'autopoïese. Son existence est bien la preuve que l'étude des changements d'échelle n'est pas propre au concept de Francisco Varela et Humberto Maturana. Ainsi, Laurent Nottale a dit au cours de son entrevue avec Réda Benkirane : « j'ai effectivement l'espoir d'utiliser ce genre de méthode dans des domaines intermédiaires. Atomes, molécule, ADN, chromosomes, noyau, cellule, tissu, organe, organisme, homme, institution, village, pays, nation, communauté – l'Europe –, planète… pour tous ces niveaux il faut arrêter d'avoir une vision réductionniste. La relativité d'échelle apporte justement ce changement mental qui permet de penser ces niveaux de réalité irréductibles les uns par rapport aux autres » (Nottale, in Benkirane, 2002, p. 350).
3.3.1.2. La théorie statistique de l'information
Cette théorie a été développée grâce à l'invention de l'ordinateur. Elle peut être considérée comme à l'origine de la complexité. Toutefois, il ne faut pas confondre cette théorie statistique de l'information avec la théorie algorithmique de l'information. Les outils de base sont les mêmes, mais leurs buts divergent.
3.3.1.2.1. Généralités sur l'information
Un bruit est « tout ce qui trouble la communication, y compris l'absence de signaux, donc même le silence » (Baylon, Mignot, 1999, p. 41).
Un message est une « succession de signaux, tiré d'un ensemble appelé répertoire, clavier ou alphabet » (Baylon, Mignot, 1999, p. 42).
Un canal est le « support physique du message » (Baylon, Mignot, 1999, p. 43). « Il est caractérisé par une capacité exprimée en bits par unité de temps » (Baylon, Mignot, 1999, p. 43).
3.3.1.2.2. La théorie statistique de l'information de Shannon
L'information n'est ni matière, ni énergie. Une information est une « valeur mathématique telle qu'il y a un rapport inverse entre probabilité des signaux et information transmise » (Baylon, Mignot, 1999, p. 41). Une distribution de probabilité discrète est un ensemble de nombres positifs pn tels que la somme de pn soit égale à 1. L'indice n va de 1 à N, où N peut être infini. « La quantité d'information est une mesure de l'imprévisibilité, de « l'effet de surprise » d'un message » (Baylon, Mignot, 1999, p. 41). La quantité d'information est définie par rapport à sa probabilité. L'information est donc liée au degré d'improbabilité. Plus l'information est improbable, plus la valeur de l'information est élevée. « L'occurrence d'un événement parfaitement prévisible n'apporte aucune information » (Baylon, Mignot, 1999, p. 41). Il faut noter que « l'information est maximale lorsque tous les éléments du répertoire sont équiprobables » (Baylon, Mignot, 1999, p. 42). La loi Wierner-Shannon exprime de la manière suivante : 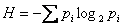 où H est l'information en bit et pi la probabilité de chaque élément. Elle mesure l'information moyenne d'un message considérée comme la quantité de hasard possible. L'information est la mesure de l'incertitude. Un théorème de Shannon introduit H comme limite inférieure du nombre de signes binaires (0 ou 1) nécessaires en moyenne pour transmettre un message dont les mots – texte sont indépendants et les mots – lexique ont les probabilités pn. D'autres démonstrations du théorème de Shannon insistent sur deux étapes intermédiaires. Si le lexique contient deux mots équiprobables, on a H = 1 ; s'il contient N mots équiprobables, on a H = log2 N. H est une mesure de la richesse du vocabulaire.
où H est l'information en bit et pi la probabilité de chaque élément. Elle mesure l'information moyenne d'un message considérée comme la quantité de hasard possible. L'information est la mesure de l'incertitude. Un théorème de Shannon introduit H comme limite inférieure du nombre de signes binaires (0 ou 1) nécessaires en moyenne pour transmettre un message dont les mots – texte sont indépendants et les mots – lexique ont les probabilités pn. D'autres démonstrations du théorème de Shannon insistent sur deux étapes intermédiaires. Si le lexique contient deux mots équiprobables, on a H = 1 ; s'il contient N mots équiprobables, on a H = log2 N. H est une mesure de la richesse du vocabulaire.
L'information pose deux problèmes essentiels : comment quelque chose sans matière et sans énergie peut-elle déterminer quelque chose ? Comment penser l'efficacité d'une information ?
Le bruit aléatoire peut modifier le message avec un mécanisme d'amplification. Deux voies permettent d'étudier la structure du bruit. La solution de la redondance consiste à prétendre que si la même information arrive au même récepteur alors elle est vraie. « Pour combattre le bruit, on introduit donc une certaine redondance dans le message. On transmet plus de signaux qu'il est nécessaire » (Baylon, Mignot, 1999, p. 43). Le phénomène est-il un ordre ou un phénomène aléatoire ? Benoît Mandelbrot (1975) a montré que les erreurs arrivent en rafale : 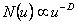 où N(u) est le nombre d'intermissions. L'apparition des erreurs correspond à une structure particulière qu'est la géométrie fractale.
où N(u) est le nombre d'intermissions. L'apparition des erreurs correspond à une structure particulière qu'est la géométrie fractale.
3.3.1.2.3. La théorie algorithmique de l'information d'Andrei Kolmogorov
« Dans la théorie ordinaire [de Claude Shannon], l'information est quantifiée par le nombre d'unités élémentaires – des bits – nécessaires pour coder cette information. Un bit, entité binaire de valeur 0 ou 1, suffit par exemple pour coder la réponse de type « oui » ou « non » à une question. L'information algorithmique d'un ensemble de données, en revanche, est définie par la taille du plus court programme nécessaire pour engendrer ces données, la taille du programme étant mesurée par le nombre minimal de bits nécessaires pour le stocker » (Chaitin, 2006, p. 70-76).
Un algorithme est composé de faits non aléatoires. Le but de la théorie algorithmique de l'information est de répondre à la question suivante : comment réduire l'information brute en une somme de 0 et de 1. « La complexité algorithmique consiste en la description de plus courte longueur d'une séquence finie donnée. Dans ce sens, une séquence totalement aléatoire générée par un bruit présente une complexité algorithmique maximum essentiellement égale à sa longueur. […] L'information sera considérée comme maximum lorsque la séquence est aléatoire étant donné que la réalisation de cette séquence particulière parmi le nombre énorme de séquences possibles revient à localiser le système de façon très pointue » dans l'espace des états. L'information est nulle dans une séquence de complexité minimum puisque le résultat que l'on est en droit d'attendre est toujours le même » (Prigogine, Nicolis, 1992, p. 247).
« Le temps ou la quantité de mémoire nécessaire n'importent pas dans la définition de l'information algorithmique, seule compte la longueur du programme » (Chaitin, 2006, p. 70-76).
« Un nombre aléatoire composé d'à peine un million de chiffres pris au hasard a un contenu en information algorithmique beaucoup plus important. Comme un tel nombre ne présente pas de régularités susceptibles de le définir, le programme le plus court pour le produire consiste à écrire explicitement la suite des chiffres. En d'autres termes, un tel flot de chiffres est incompressible et ne contient aucune redondance. De tels nombres sont dits irréductibles ou algorithmiquement aléatoires » (Chaitin, 2006, p. 70-76).
3.3.2. Le chaos
« Découvrir, c'est souvent voir autrement »
(Nottale, 1998, p. 110).
La théorie du chaos4 s'est développée aux Etats-Unis et en Europe vers la fin des années 1960. Cette théorie s'applique sur les structures dissipatives ou sur les systèmes dynamiques. Elle repose sur l'idée d'un système déterministe. Le chaos est une évolution temporelle avec dépendance sensitive des conditions initiales (David Ruelle). On répertorie deux types de chaos : le « chaos déterministe » et le « chaos stochastique ». Pour le chaos déterministe, le désordre résulte d'un processus rigoureusement défini. « Le déterminisme peut produire des résultats non prévisibles » (Dauphiné, 1995, p. 17). Pour le chaos stochastique, le désordre est dû à une multitude de causes agissant sans aucun lien entre elles. Il n'existe pas de définition claire du terme « chaos », mais on rapproche le chaos d'un phénomène de turbulence. Toutefois, on connaît, au moins, trois types de routes de processus, menant à un chaos. Le premier scénario explique que la turbulence apparaît dans un système après trois bifurcations à partir d'un état stationnaire. Ce sont les travaux de David Ruelle et de Floris Takens (1971) (Ruelle, 1991). Ces chercheurs ont lancé l'idée d'attracteurs étranges. Un attracteur est un espace théorique constitué d'un ensemble de points correspondant aux états possibles du système, distribués selon une topologie. Le premier attracteur a été construit par Edward Lorenz, celui qui a écrit « un battement d'ailes de papillon en Chine peut provoquer un ouragan en Californie ». Il est vrai que son attracteur explique que l'on ne peut pas prévoir le temps qu'il fera demain ou après demain. Cela est lié à la complexité de l'attracteur qui est très développée. Les attracteurs ne sont pas seulement de nature chaotique. Il en existe quatre types : le point, le cycle, le tore et les attracteurs étranges, qui sont généralement fractales. Le deuxième scénario repose sur le mécanisme de doublement de période (Mitchell Feigenbaum). Ce scénario utilise ce que l'on appelle la méthode logistique de Verhulst (1838). Le troisième scénario repose sur la notion d'intermittence (Yves Pomeau et Paul Manneville [Manneville, 1991]), qui recouvre un phénomène relativement simple : un système devient turbulent lorsqu'il a été envahi par des fluctuations « anormales ». La multiplication de ces fluctuations anormales dans le temps aboutit par étapes successives à la turbulence à proprement dite. Cependant, il faut remarquer que les trois scénarios ne sont pas incompatibles. Autrement dit, décrire et expliquer un système chaotique demande une approche de nature structurelle.
| Les routes possibles | Les principaux découvreurs |
|---|---|
| La route par bifurcations successives | FEIGENBAUM COULLET TRESSER |
| La route par le passage d'attracteurs périodiques à des attracteurs étranges (avec un nombre fini de bifurcations selon le scénario de ces découvreurs) | RUELLE TAKENS NEWHOUSE |
| La route par apparition d'un régime dynamique intermittent | POMEAU MANNEVILLE |
Il existe quelques néologismes propres au chaos comme chaologie qui est l'étude du chaos, ou chaotique qui est l'adjectif désignant un phénomène relevant du chaos, ou encore chaométrie qui désigne les mesures faites du chaos. Les différents concepts que nous allons aborder ont tous un point commun : ils présentent la particularité d'être apparemment discontinus.
Toutefois, la célèbre phrase d'Edward Lorenz (1963) a été, en partie, remise en cause par la notion d'horizon de prévisibilité. Il s'agit de dire qu'un système chaotique possède un comportement qui peut permettre de déterminer son état à une date plus ou moins éloignée. Il permet de caractériser le futur d'un système chaotique. L'horizon de prévisibilité pour les prévisions météorologiques est de l'ordre de trois à cinq jours, par exemple. Cet horizon est dû au fait que l'information que nous détenons, qui devrait être, en théorie, infinie pour un système chaotique, sera toujours imparfaite. Ce qui implique que l'on introduit, involontairement, une erreur dans la position de l'état initial du système à partir de laquelle sont effectués les calculs. Autrement dit, un système chaotique est très sensible aux conditions initiales que l'on impose à ce calcul. Ce qui implique que la prise en compte d'un écart faible sur une variable peut donner des résultats radicalement différents. Une petite cause peut générer un grand effet. C'est tout le sens de la citation d'Edward Lorenz. Il existe une autre source d'incertitude qui conduira le système vers un état étonnant. Elle s'introduit dans le calcul même lors, par exemple, d'une multiplication des nombres non entiers, le nombre de chiffres après la virgule est lui aussi multiplié. Or, sauf à saturer la mémoire du calculateur de chiffres après la virgule, ce qui est contraire au but recherché, il faut à un moment ou à un autre arrondir, couper, donc introduire une erreur qui inévitablement fera diverger le système. Le rapport entre cause et conséquence n'est plus linéaire ou continu : il est non linéaire ou discontinu. La divergence peut être elle-même calculée par ce que l'on appelle les exposants de Lyapounov, ce qui permet d'établir la vitesse de divergence du système.
Le domaine de l'aléatoire ressort de tout cela de plus en plus réduit. Si on ajoute que le chaos est un modèle qui peut être appliqué dans de nombreux domaines scientifiques comme la circulation atmosphérique, la société, le réseau Internet… Il apparaît que ce mode de connaissance change radicalement notre façon d'aborder le monde. Cela étant, la non linéarité d'un phénomène permet au système chaotique de produire de la variété, donc l'adaptation qui lui est nécessaire. Un système non chaotique à comportement linéaire lui ne peut produire autant de variétés. Autrement dit, appliquer aux sciences humaines, un système social chaotique devrait être plus robuste qu'un système social non chaotique, beau paradoxe par rapport au sens commun. Le problème, au fond, est que le passé du système ne permet pas de se projeter dans l'avenir, puisqu'il peut bifurquer n'importe quand : aujourd'hui même, demain, après demain, dans cent ans… Pour Etienne Klein, grâce aux systèmes chaotiques, on peut dire qu'« il n'y a pas de flèches du temps, seul le niveau global donne l'impression qu'il y en a une » (Prigogine, in Klein, 1995, p. 40). Ce qui implique que c'est parce que l'espace est en mouvement que le temps existe. Peut-on dès lors instrumentaliser le chaos ? Ce serait un rêve de pouvoir dire quand le système va bifurquer, puisque l'on pourrait se positionner avant la bifurcation et choisir la direction que l'on veut faire prendre au système. Dans l'état des travaux actuels, cela demeure un beau rêve, malgré les recherches de Laurent Nottale (1993 ; 1998 ; 2000) qui vont dans ce sens. Il serait trop simple et trop facile de penser que, pour tout, une fois le programme trouvé, on puisse faire des prévisions. En effet, un programme générant un chaos évolue aussi dans le temps. Il provoque ce que les physiciens appellent une brisure de symétrie. Pascal Chossat (1996) rappelle que ces brisures se font de manières spontanées. Autrement dit, les bifurcations sont imprévisibles. Ce sont des catastrophes au sens de René Thom.
3.3.2.1. Les systèmes déterministes
Un système déterministe est un « système modélisé par des équations qui ne font pas intervenir de variables aléatoires, c'est-à-dire de fluctuations gouvernées par une loi de probabilité » (Chossat, 1996). Dans le cadre déterministe, les certitudes sont possibles. L'incertitude serait posée dans un cadre non déterministe par nature. Cependant, il existe une position intermédiaire : celle du chaos. En effet, le chaos prouve que « le déterminisme peut produire des résultats non prévisibles » (Dauphiné, 1995, p. 17). On peut citer comme exemple le comportement d'un système dissipatif et/ou dynamique qui montre que « le point fondamental [du chaos] est la reconnaissance que des systèmes simples, déterministes peuvent avoir un comportement apparemment aléatoire » (Sapoval, 1997, p .230).
3.3.2.2. La non linéarité
« Tout le progrès de la science était fondé sur la croyance que la manière de chercher la simplicité dans la nature était de trouver des équations simples pour la décrire. Quelle question stupide. » (Stewart, 1998, p. 88). La forme la plus simple est bien entendu l'équation linéaire. « Une équation est linéaire si la somme de deux solutions est encore une solution » (Stewart, 1998, p. 97-98). Cependant, « la linéarité est un piège » (Stewart, 1998, p. 126), car la physique, par exemple, a été bâtie sur des théories ayant un espace à deux dimensions, alors que la réalité est un espace à trois dimensions, voire quatre (Albert Einstein) ou cinq (Laurent Nottale).
De plus, la réalité des phénomènes qui nous entourent n'est pas linéaire : elle est non linéaire. « La non linéarité signifie que le fait de jouer modifie les règles du jeu : l'importance du frottement dépend du palet qui, à son tour dépend du frottement » (Gleick, in Dauphiné, 1995, p. 19).
3.3.2.3. La dynamique
Toutefois, le chaos n'apparaît que pour les systèmes ouverts, c'est-à-dire soumis à une force extérieure qui permet de leur réinjecter l'énergie perdue par la dissipation. Par définition, les systèmes ouverts n'atteignent jamais un état d'équilibre.
>Les dynamiques d'un système sont décrites par la thermodynamique. La thermodynamique est simplement la mécanique statistique. Il y a deux branches dans cette science : la thermodynamique proche de l'équilibre et la thermodynamique très loin de l'équilibre. La première est la plus connue. Elle repose sur les lois de conservation de l'énergie de James Joule (1842) et cherche à transformer l'énergie thermique en énergie mécanique. Rudolf Clausius formule, en 1865, la loi de croissance irréversible de ce que l'on appelle l'entropie qui est une fonction caractérisant l'état de désordre de la matière. Quand la température baisse, l'entropie augmente, et réciproquement. La thermodynamique proche de l'équilibre repose sur l'idée que le système est fermé, ce qui signifie qu'il n'a aucun contact avec son environnement. Autrement dit, il n'y a pas de flux de matière, d'énergie et d'information.
C'est pour cela que l'on a développé depuis 1945, la thermodynamique très loin de l'équilibre, qui décrit les systèmes ouverts, non conservatifs, c'est-à-dire dissipatifs. En effet, il faut constater que l'évolution du monde tend vers l'ordre, plutôt que vers le désordre, or la thermodynamique montre le contraire : on devrait aller de l'ordre au désordre. L'expérience type matérialisant ce phénomène de passage de l'ordre au désordre et du désordre à l'ordre, est ce que l'on appelle les cellules d'Henri Bénard (1900). Il s'agit de chauffer régulièrement une couche mince d'un liquide homogène entre deux plaques, la plaque inférieure étant chauffée, la plaque supérieure restant froide. Il y a donc un gradient de température entre les deux. Quand le gradient dépasse une certaine valeur, des cellules de convection se déploient rapidement. Elles fonctionnent par couple, l'une d'elle tournant de droite à gauche, l'autre tournant de gauche à droite. C'est un phénomène type d'auto organisation. Les structures dissipatives correspondent donc à l'émergence, apparemment spontanée, d'un ordre. Si la température continue à augmenter, les deux cellules vont se complexifier en reproduisant leur forme initiale à une échelle inférieure, et ainsi de suite, jusqu'à la création d'un phénomène de turbulence. Il s'agit d'une évolution temporelle irrégulière et de structures spatiales « décorrélées », c'est-à-dire évoluant indépendamment les unes des autres et devenant pratiquement impossible à identifier (Chossat, 1996). La turbulence est un jeu d'échelles. Elle peut être décrite par la géométrie fractale. On voit donc une cascade de cellules dans l'ordre des échelles. Pour annuler cette complexification croissante, il suffit simplement de faire baisser le gradient de température. Il faut remarquer que l'on passe d'un état à un autre brusquement, sans aucun pallier avant la bifurcation du système. L'état, immédiatement antérieur à la bifurcation, est ce que l'on appelle un état critique, matérialisé par une agitation anormale des molécules. On constate que les systèmes agissent afin d'assurer le transport de l'énergie, c'est-à-dire, en fait, sa dégradation rapide. Cet état critique montre que les causes de l'émergence d'un nouveau système sont essentiellement internes. Toutefois, il y a quelques contraintes externes dans la formation de ces cellules : la gravité, par exemple. Les cellules n'apparaissent pas en apesanteur.
3.3.2.4. Les structures dissipatives
L'ordre dans les cellules d'Henri Bénard est à la fois de nature temporelle et de nature spatiale, mais « contrairement aux structures d'équilibre qui, une fois créées, n'ont pas besoin d'un apport d'énergie extérieure pour se maintenir, les structures dissipatives sont formées et stabilisées par les flux de matière et d'énergie qu'elles échangent avec le milieu qui les entoure » (Boutot, 1993, p. 48). La thermodynamique montre que l'évolution tend irréversiblement vers un équilibre décrit comme la « mort thermodynamique de l'univers », ce qui est en opposition avec l'idée de Charles Darwin, puisque dans la thermodynamique, le seul événement qui peut avoir un sens est le moment où le système atteint son équilibre. L'évolution de système dissipatif, en physique, est supposée déterministe. Cependant, le concept de structures dissipatives dépasse le champ de la physique. « En biologie, [par exemple] quand vous atteignez un équilibre, vous êtes mort » (Gleick, 1991, p. 373). Le cas le plus classique est le cœur (humain). Il possède un rythme chaotique. Si ce rythme atteint l'équilibre (le point), l'individu est meurt !
3.3.2.5. L'entropie
Les sciences de la complexité ont davantage exploré le concept d'entropie qui prend désormais trois grandes dimensions.
C'est la physique statistique qui inventa le concept. L'entropie, dans la seconde loi de la thermodynamique, mesure le gain de chaleur. De plus, cette seconde loi de la thermodynamique a formalisé mathématiquement l'irréversibilité par ce concept (Le Méhauté et alii, 1998). L'entropie est un bilan concernant la variation d'une fonction d'état S suivant l'équation  , ce qui signifie que la variation dSe due à l'échange d'énergie et de matière entre le système et son environnement, et la variation dSi due à la création ou à la disparition d'entropie au sein du système. Si dSi est strictement positive alors on a à faire à une transformation irréversible spontanée où l'entropie croît de manière strictement positive. Si dSi est nulle alors on a une transformation réversible. Enfin, il faut remarquer qui si dSe est nulle alors le système est isolé.
, ce qui signifie que la variation dSe due à l'échange d'énergie et de matière entre le système et son environnement, et la variation dSi due à la création ou à la disparition d'entropie au sein du système. Si dSi est strictement positive alors on a à faire à une transformation irréversible spontanée où l'entropie croît de manière strictement positive. Si dSi est nulle alors on a une transformation réversible. Enfin, il faut remarquer qui si dSe est nulle alors le système est isolé.
Lorsque dSi est strictement positive, l'entropie devient une mesure du désordre, suite à la perte d'énergie. On peut alors formuler Si telle que :
Si = –k ln W
où W est le nombre de configuration atomique possible du système et k une constante (celle de Boltzmann pour un gaz par exemple). La thermodynamique montre que l'état le plus probable dans le monde est le désordre. Autrement dit, « l'entropie mesure la quantité de hasard présente dans un système » (Ruelle, 1991, p. 137).
Claude Shannon transforme l'entropie en une quantité d'information :
I = –k ln M
avec M le nombre de messages possibles en bits. De plus, Claude Shannon démontre grâce à cette formule que l'état le plus probable de l'information est le bruit !
En géographie, « l'entropie spatiale » reste à définir précisément. Cependant, sa forme mathématique sera identique aux équations précédents : une variable V à définir, une variable de mesure M et une constante k.
V = –k ln M
Avec la théorie de la relativité d'échelle, il est possible d'identifier une telle relation, du moins hypothétiquement. V pourrait correspondre à la distance et M à la résolution. Ce qui revient à dire que, si toutes les échelles sont présentes alors l'entropie est maximale, et inversement, si quelques échelles sont présentes alors l'entité considérée est organisée. Fondamentalement l'ordre morphologique que nous permet de comprendre la théorie de la relativité d'échelle est un ordre des gammes d'échelles. Ainsi, il existerait ce que Laurent Nottale appelle des « échelles de coupure ». À partir d'une échelle minimale, l'objet existe et possède une morphologie descriptible, tandis qu'au-delà d'une échelle maximale, l'objet n'existe plus : il n'a plus de morphologie propre c'est-à-dire qu'il se trouve englober dans une autre structure plus grande ou plus petite selon les cas.
Yvon Gauthier résume bien l'évolution du concept d'entropie. « Le concept d'entropie est apparu dans la théorie de la chaleur pour ensuite passer à la théorie de l'information et revenir à la théorie probabiliste des systèmes dynamiques (ergodiques) » (Gauthier, texte pdf).
3.3.2.6. L'attracteur
Le concept d'attracteur est flou puisque, comme le dit James Stewart (1998, p. 162), il s'agit de tout et de n'importe quoi du moment que tout y converge. Toutefois, cette convergence se réalise au sein d'un espace des phases (ou de configuration) qui correspond à la mise en corrélation de la position et la vitesse, c'est-à-dire entre x et 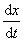 . Plus généralement, il s'agit de faire correspondre une variable x avec la dérivée de cette variable x par rapport à une autre grandeur. Ainsi, un espace des phases en échelle correspond à la mise en corrélation entre x et
. Plus généralement, il s'agit de faire correspondre une variable x avec la dérivée de cette variable x par rapport à une autre grandeur. Ainsi, un espace des phases en échelle correspond à la mise en corrélation entre x et 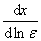 , c'est-à-dire la variable x et la dérivée de cette variable x par rapport au logarithme de la résolution. Il existe quatre grands types d'attracteurs : le point, le cercle (ou l'ellipse), le tore et le chaos.
, c'est-à-dire la variable x et la dérivée de cette variable x par rapport au logarithme de la résolution. Il existe quatre grands types d'attracteurs : le point, le cercle (ou l'ellipse), le tore et le chaos.
L'attracteur exprime l'état d'une dynamique. Celle-ci s'exprime soit en termes de stabilité, soit en termes d'instabilité. La stabilité maintient un système dynamique dans son état : une perturbation ne modifierait pas son fonctionnement. La stabilité peut être illusoire car le système peut évoluer dans le temps mais à l'état d'équilibre. L'instabilité regroupe tous les cas où la perturbation modifierait la dynamique du système. Comment évaluer le résultat d'une perturbation ! On choisit un état de référence arbitrairement Xs comme attracteur. Soit une perturbation x(t) telle que X(T) = Xs + x(t). Il existe quatre solutions possibles au sens de Lyapounov : le cas stable, le cas asymptotiquement stable, le cas de l'instabilité et le cas localement stable, mais globalement instable. Cela est mesuré par le nombre caractéristique de Lyapounov.
Il existe deux types de temps possibles : le temps polynomial (celui de la théorie algorithmique de l'information ou le temps exponentiel (Lyapouvov). On définit le nombre caractéristique (ou exposant) de Lyapounov tel que :
où τ est appelé le temps de Lyapounov qui donne une mesure de l'horizon de prévisibilité. Plus il est élevé, plus la dynamique du système est stable.
3.3.3. Les fractales
Le terme « fractal » vient de l'adjectif latin fractus (fracture) et du verbe frangere (briser). Etymologiquement, fractal veut donc dire fraction et/ou fracture.
La géométrie fractale est un des outils qui permet de mesurer le chaos, ou plutôt qui essaye de le quantifier. Cependant, elle peut être considérée comme une manière de voir le monde, indépendante du chaos. C'est pour cela que chaoticiens et fractalistes expriment les mêmes idées, mais n'ont pas la même priorité. Les premiers étudient la dynamique des systèmes, les seconds étudient la structure des systèmes (Stewart, 1998, p. 308).
Traditionnellement nous utilisons, pour décrire les formes que nous voyons la géométrie euclidienne composée par les figures classiques (carré, cercle, triangle, polygones divers…). Depuis une trentaine d'années, la géométrie euclidienne ainsi que la première géométrie non euclidienne, la géométrie riemannienne (début XXe siècle) ont été englobées, dépassée par la deuxième géométrie non euclidienne : la géométrie fractale (années 1950). Celle-ci étudie toutes les formes irrégulières, ou qui nous apparaissent comme telles. « Les fractales sont des objets – qu'ils soient mathématiques, dus à la nature ou dus à l'homme – qu'on appelle irréguliers, rugueux, poreux ou fragmentés, et qui, de plus, possèdent ces propriétés au même degré à toutes les échelles. C'est dire que ces objets ont la même forme qu'ils soient vus de près ou de loin » (Mandelbrot, 1997, p. 33). Notre réflexion nous conduira à corriger cette définition.
Le principal outil est ce que l'on appelle la dimension fractale ou plutôt les dimensions fractales qui présentent la particularité d'être parfois non entières. Rappelons qu'Euclide et ses successeurs avaient défini les dimensions mathématiques comme étant strictement entières : la dimension zéro correspondant aux points, la dimension une aux courbes, la dimension deux aux surfaces et la dimension trois aux volumes. Depuis, on a ajouté à ceux-ci l'espace-temps à quatre dimensions d'Albert Einstein et l'espace-temps fractal à cinq dimensions de Laurent Nottale. Ce concept de dimension au sens d'Euclide ne pouvait cependant définir que des figures que nous qualifierons de régulières, créées généralement par les hommes oubliant que la nature aime l'irrégularité. Ainsi, les dimensions fractales qualifient tous ces objets oubliés. Il s'agit d'un « nombre qui quantifie le degré d'irrégularité et de fragmentation d'un ensemble géométrique ou d'un objet naturel, et qui se réduit, dans le cas des objets de la géométrie usuelle d'Euclide, à leurs dimensions usuelles » (Mandelbrot, 1975, p. 155). Ce mémoire présentera la relativité d'échelle de Laurent Nottale qui est une extension de la théorie mathématique de Benoît Mandelbrot.
3.4. Conclusion de la partie
Tenter de comprendre la complexité, c'est d'abord d'accepter de renoncer partiellement aux quatre préceptes de René Descartes, mais surtout mettre fin à la dichotomie de la logique formelle d'Aristote. C'est prendre conscience que notre science a ses limites et qu'elle n'est pas inébranlable. Ce n'est qu'une forme de croyance raisonnable, ce qui signifie qu'elle peut se tromper. La géographie a participé de près ou de loin à ces débats, sans vraiment faire entendre sa voie. Comment peut-on faire entrer la géographie dans les sciences de la complexité ?
4. Géographie et échelles
Si peu de géographes se reconnaissent dans les sciences de la complexité, il n'en demeure pas moins que la géographie a été précurseur dans le domaine. En effet, le géographe sait très bien, et ce depuis l'école vidalienne, qu'observer un espace géographique au 1/50 000 n'est pas la même chose qu'observer le même espace au 1/100 000. Autrement dit, intuitivement, le géographe constate que « l'information dépend de l'échelle à laquelle on la perçoit ». Cependant, quel est le lien profond entre l'information et l'échelle .
L'analyse spatiale a tenté de clarifier les concepts d'espace et d'espace géographique. Cependant, elle n'a pas rejetée la notion d'échelle. L'obsession de trouver la bonne échelle pour tel ou tel espace géographique demeure au cœur de l'analyse géographique en général.
L'échelle choisie va également influencer la limite naturelle ou anthropique. Par exemple, le tracé de la frontière de la France ne sera pas le même si l'on est à 1/50 000 ou si l'on est à 1/1 000 000 ! Pourtant, il s'agit bien de représenter la France sur l'interface terrestre. Autrement dit, la précision du tracé est une notion d'échelle. Pendant longtemps, la géographie s'était plus attardée sur les problèmes de projection, mais elle avait conscience de ce qu'elle avait appelé « l'effet d'échelle » c'est-à-dire le fait de gagner ou de perdre de l'information géographique en passant d'une échelle à une autre. Quel est le lien entre espace et échelle .
La géographie gagnerait donc à étudier les liens entre échelle et limite ou, plus exactement, entre échelle et morphogenèse. Un outil permettant de faire le lien entre échelle et limite existe déjà : il s'agit de la géométrie fractale bien entendu. Cependant, il faut, au préalable, construire la géographie en tant que science autonome, et non plus science carrefour.
4.1. Construction de l'espace géographique et de l'objet de la géographie
4.1.1. Construction de la démarche scientifique en géographie
La première étape consiste à définir des variables, ou plus exactement des grandeurs qui vont servir de quantifications des mesures faites en géographie. C'est un exercice extrêmement difficile qui suscite de nombreux tests, mais surtout de nombreuses déceptions et vexations. Cela étant, une fois la relation découverte, il faudra rechercher des corrélations entre ces grandeurs.
Autrement dit, il faut rechercher un modèle mathématique traduisant cette corrélation. On peut dès lors étudier analytiquement ce modèle. Cela consiste d'abord à étudier la fonction définie par le modèle, ce qui en soi n'est pas très difficile. Cependant, il faut également trouver la cause de cette fonction, ce qui est moins évident. Cela se fait grâce à des outils mathématiques comme les équations différentielles. Toutefois, il n'est pas rare qu'il faille construire de nouveaux outils mathématiques pour trouver cette causalité.
Enfin, il faut conclure par la construction théorique de ce que l'on a observé en pratique, mais surtout, par l'interprétation qualitative de cette ou ces relations. Ces relations permettront d'en établir d'autres purement théoriques. Cependant, elles pourront aussi être invalidées, auquel cas, il faudra rechercher une nouvelle écriture mathématique pour faire face à ce que l'on a observé de contradictoire.
4.1.2. Construction des principes premiers de la géographie
Rappelons qu'un principe est une proposition qui ne fait pas remonter à d'autres propositions appartenant au même domaine scientifique. Il n'est ni démontré ni démontrable. Autrement dit, une fois posé, il reste parfaitement réfutable et contestable. Il s'agit ici de présenter les principes de premier ordre qui sont, par définition, « les principes logiques que l'on peut déduire par induction et que l'on ne peut pas vérifier expérimentation avec certitude ». Ils obéissent au dilemme d'Agrippa : ou bien la connaissance est fondée sur des principes premiers, mais arbitraire, ou bien on ne trouve pas de tels principes et on a une régression à l'infini, ou bien la justification est circulaire.
4.1.2.1. Les principes premiers philosophiques
4.1.2.1.1. Le principe de causalité
Le principe de causalité a été formulé par Aristote. Il exprime l'idée que toute cause entraîne un effet, et que tout effet trouve son origine dans une cause. Depuis, l'approche systémique a ajouté à ce principe, la causalité circulaire où l'effet entraîne de nouveau la cause qui l'a produit. Ce principe a pour corollaire le principe de certitude : si j'ai les conditions initiales A alors j'obtiendrais B. C'est une certitude ! De plus, il faut précise que le principe de causalité s'exprime dans un cadre évidemment déterministe.
Le principe de causalité est extrêmement simple, mais comment respecter mathématiquement ce principe ? La mathématisation du principe de causalité a été très difficile. Un certain Isaac Newton a eu l'idée de relier ce principe de causalité à la théorie mathématique de la dérivabilité et de la différentiabilité. Il faut dans un premier temps revenir sur la définition d'une fonction f et de sa fonction dérivée f' ![]() . On appelle fonction f une relation où chaque élément de l'ensemble de départ possède au plus une image dans l'ensemble d'arrivée. On suppose que f est définie au voisinage de x0. On dit que f est dérivable en x0 si le quotient
. On appelle fonction f une relation où chaque élément de l'ensemble de départ possède au plus une image dans l'ensemble d'arrivée. On suppose que f est définie au voisinage de x0. On dit que f est dérivable en x0 si le quotient ![]() admet une limite finie lorsque x tend vers x0. La fonction dérivée f' permet de connaître la variation de la fonction f. En effet, si f' est positif sur un intervalle I alors f est croissante sur I. Si f' est négatif sur un intervalle I alors f est décroissante sur I. si f' est nulle sur un intervalle I alors f est constante sur I (Bourbaki, 1961 ; Schwartz, 1961 ; Bass, 1964 ; Cartan, 1967 ; Martin, 1967 ; Bass, 1968-1971 ; Smirnov, 1969 ; Ayrès, 1972 ; Flory, 1974, Ayrès, Schmidt, 1978 ; Dameron, 1994-1997 ; Pham, 1996).
admet une limite finie lorsque x tend vers x0. La fonction dérivée f' permet de connaître la variation de la fonction f. En effet, si f' est positif sur un intervalle I alors f est croissante sur I. Si f' est négatif sur un intervalle I alors f est décroissante sur I. si f' est nulle sur un intervalle I alors f est constante sur I (Bourbaki, 1961 ; Schwartz, 1961 ; Bass, 1964 ; Cartan, 1967 ; Martin, 1967 ; Bass, 1968-1971 ; Smirnov, 1969 ; Ayrès, 1972 ; Flory, 1974, Ayrès, Schmidt, 1978 ; Dameron, 1994-1997 ; Pham, 1996).
Dans tous les problèmes pratiques, on connaît f' qui est le modèle mathématique que l'on évalue statistiquement dans la plupart des cas. Autrement dit, f' est la conséquence (ou l'effet) du comportement de la fonction f. En effet, quel que soit le phénomène étudié, nos sens ne peuvent en percevoir que la conséquence, c'est-à-dire, déjà, une interprétation particulière qu'il faut ressentir ! Il faut donc déterminer f. Pour ce, il faut utiliser les méthodes de l'intégration. Intégrer ou trouver une primitive, on consiste à trouver une fonction F(x) qui a pour dérivée la fonction de départ f. C'est le calcul intégral qui va permettre de trouver les fonctions f possibles. En effet, cette méthode ne permet malheureusement pas de trouver une unique fonction f, mais de déterminer la forme générale de cette fonction avec des paramètres à évaluer pour obtenir la solution de notre problème. Cependant, il est très difficile de trouver des causalités « simples ». Très souvent, il faut réintégrer la fonction f pour trouver une cause plus profonde, etc. Le problème de la cause première s'exprime donc ici de la manière suivante : où doit-on arrêter d'intégrer ? En physique, il est extrêmement rare de dépasser la « primitive seconde ». L'archétype est la trajectoire : à partir de conditions initiales, on détermine l'accélération, on l'intègre : on détermine alors la vitesse, on intègre de nouveau et on trouve la position. La cause première de cet exemple est donc la position x par rapport au temps t.
Là, entre en scène les équations différentielles pour sélectionner des fonctions dans cette infinité qui permettent de coupler plusieurs causes et effets c'est-à-dire plusieurs fonctions dérivées et/ou primitives. Aussi, un outil pratique a été inventé par Isaac Newton et Gottfried Wilhem Leibniz : le calcul différentiel. Il n'est pas facile de comprendre de prime à bord ce qu'il signifie. Cependant, on peut dire que c'est une sorte de résumé de l'intrigue. En effet, en une ligne d'équation, on résume le ou les effets observés par la ou par les causes déterminées. Par exemple, pour les fractales, nous verrons dans la quatrième partie que l'équation de base
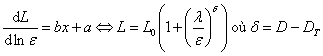 où
où 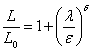
exprime l'idée que la cause de la fractalité exprimée par une fonction L quelconque, est la dépendance d'échelle de cette fonction exprimée par le logarithme népérien de la résolution ε, c'est-à-dire de l'étalon servant à effectuer la mesure. L'échelle devient donc par cette équation simple, cause de la fractalité, et plus généralement, nous le verrons par la suite, des phénomènes chaotiques et quantiques. La dimension fractale D devient un paramètre de contrôle de la manifestation de la fractalité, élément que vous ne trouverez pas chez Benoît Mandelbrot, par exemple. Toutefois, cette méthode pose le problème de la cause première car, mathématiquement, on pourra toujours trouver des dérivées ou des primitives. À un moment, il faudra donc s'arrêter et admettre que l'on a trouvé, du moins provisoirement, la cause profonde de ce que l'on a observé. En physique, il est rare d'avoir plus de deux dérivations de la même fonction.
Il existe de nombreux autres outils mathématiques qui permettent de respecter ce principe, mais aucun n'a la puissance du calcul différentiel. En effet, l'expression cause – conséquence dans une unique équation permet de comprendre et de fabriquer une dynamique. Aussi, la découverte des fractales et la « découverte » du chaos avaient mis à mal cet outil. Dans le cas des fractales, la non différentiabilité est une caractéristique, donc les équations différentielles ne semblent pas à première vue s'appliquer. Pour les phénomènes chaotiques, les équations différentielles perdent leur « causalité-effet » dans la mesure où leur résultat devient imprévisible. Nous verrons par la suite que la théorie de la relativité d'échelle permet de rétablir ce principe, donc qu'elle a le pouvoir de le maintenir en géographie.
4.1.2.1.2. Le déterminisme
Il ne faut pas confondre le déterminisme et la causalité. Le déterminisme apparaît vers 1820. Il s'agit de comparer le monde à une machine. Le déterminisme est appliqué à l'univers. On confond également le déterminisme partiel et scientifique du postulat méthodologique qui consiste à isoler un groupe de phénomènes pour en découvrir les lois, et le déterminisme universel qui est une hypothèse métaphysique impliquant une prise de position totalitaire, étrangère à la science. Le déterminisme partiel et scientifique postule la prévisibilité et s'oppose à une certaine conception métaphysique du hasard. Le déterminisme universel nie notre intuition de la liberté, en réduisant toute activité à des interactions mécaniques.
Le déterminisme au sens strict de Pierre-Simon Laplace implique la connaissance de toutes les conditions initiales et de toutes les interactions agissantes. Cependant, il est impossible de connaître la totalité de celles-ci. Autrement dit, le déterminisme absolu n'a pas de sens. La vérité est devenue relative.
4.1.2.1.3. Le principe de la raison suffisante (Leibniz)
Le principe de la raison suffisante s'énonce de la manière suivante : « toute proposition analytique est vraie ». Autrement dit, il suffit de formuler un phénomène par une fonction mathématique pour qu'il devienne vrai. Il repose sur d'autres principes comme celui de la continuité ou de non contradiction. Le principe de non contradiction s'exprime de la manière suivante : « il est impossible que P et sa négation soient vraies en même temps ». Cela donne l'exemple du rapprochement entre le principe de causalité et la théorie mathématique des dérivées et des équations différentielles.
4.1.2.1.4. Les principes téléologiques
Contrairement, à ce que l'on lit trop souvent, ces principes ne sont pas nés avec la systémique. Ils sont parfois très anciens (Molk, 1991). Pour répondre à un souci de clarté, ce mémoire ne va développer que le principe de moindre action ou d'économie ou principe variationnel (1744) de Pierre Louis Moreau de Maupertuis.
Le principe de moindre action constitue un des tous premiers principes téléologiques formulés dans la science. Il s'exprime de différentes manières, tant d'un point de vue littéraire que d'un point de vue mathématique. Tout commence avec la définition d'une action. L'action correspond à une quantité de travail ou à une énergie multipliée par une durée (temps) ou à une impulsion multipliée par une longueur (espace). Cette grandeur est construite à partir des différentes variables qui définissent un système dynamique. L'étude des valeurs extrêmes qu'elle peut prendre permet de raisonner sur l'évolution du système considéré.
Pierre de Fermat, vers 1650, avait formulé le premier principe minimum en remarquant que la lumière voyage toujours d'un point à un autre en minimisant son temps de trajet. Cependant, c'est bien Pierre Louis Moreau de Maupertuis qui généralise ce principe. Pour ce dernier, l'action est égale au produit de la masse d'un corps par l'espace qu'il parcourt et par sa vitesse. Ainsi, « les phénomènes naturels adviennent de manière à minimiser le produit m.v.s. de la masse, la vitesse et la distance » (Odifreddi, 2004, p. 50). Dès lors, le principe de moindre action peut se formuler de la manière suivante : « dans les changements qui se font dans l'état d'un corps, la quantité d'action nécessaire pour produire ce changement, est la moindre qu'il est possible » c'est-à-dire les chemins les plus simples, les plus directs et les plus « efficaces ». En 1788, Joseph Louis de Lagrange trouva une expression mathématique générale formulant le plus généralement possible ce principe. Toutefois, ce principe s'est heurté à la mécanique quantique dans laquelle il ne semblait plus respecter. C'est Richard Feynman qui formula la version quantique du principe via ce que l'on appelle la « méthode de l'intégrale de chemin ». Aujourd'hui, ce principe a eu tendance à segénéraliser dans d'autres disciplines que la physique comme en économie ou en géographie.
4.1.2.1.5. Le principe de relativité (Galilée, Einstein, Poincaré, Nottale)
Le principe de relativité s'énonce de la manière suivante : « les lois de la nature doivent être valides dans tous les systèmes de références (le référentiel), quel que soit leur état » (Einstein, 1916, in Nottale, 1998, p. 7). Le système de référence est le système de coordonnées. Ainsi mesurer une position entraîne une différence entre au moins deux points. De même pour le mouvement, seule une différence de vitesse a un sens, jamais une vitesse absolue.
La relativité est un principe de la physique moderne qui existe depuis Galileo Galilei qui a découvert que « le mouvement est comme rien » (Galilée, in Nottale, 1998, p. 7). « Le mouvement ou le repos n'ont aucune existence propre, seul a un sens le mouvement d'un corps relativement à un autre. Seules comptent les relations deux à deux entre les objets, non leurs propriétés absolues, qui sont dénuées de signification physique » (Nottale, 1998, p. 7).
La relativité restreinte a été découverte indépendamment par Henri Poincaré et par Albert Einstein. Elle établit que l'on peut mesurer l'espace et le temps avec la même unité. D'ailleurs, depuis 1985, le Bureau international des poids et mesures ne sépare plus l'unité de l'espace et l'unité du temps ; ce n'est qu'une seule unité de temps.
La relativité générale montre que « la gravitation n'existe pas en soi, mais que son existence même dépend du choix du référentiel » (Nottale, 1998, p. 70). La gravitation devient relative. « Albert Einstein a été amené à postuler que la gravitation et la géométrie ne sont finalement qu'une seule et même chose. C'est précisément à un tel énoncé qu'arrive finalement la théorie de la relativité générale, en identifiant les effets de la gravitation aux manifestations de la courbure de l'espace-temps » (Nottale, 1998, p. 75).
Galileo Galilei, Henri Poincaré et Albert Einstein ont créé une relativité du mouvement. Un objet peut être en mouvement dans un référentiel et immobile dans un autre. C'est le cas de tout passager d'une automobile qui est en mouvement par rapport à la route mais pas par rapport à la voiture.
Cela étant comme le note Laurent Nottale : « Un sens beaucoup plus général peut être donné au principe de relativité, grâce à une extension de la notion de système de référence » (1998, p. 89). Ainsi faut-il distinguer le principe de relativité, des théories qui ont été construites à partir de lui. « L'idée est que le principe de relativité ne s'applique pas seulement au mouvement, mais à toutes les grandeurs qui caractérisent l'état (lequel est toujours relatif) du système de référence » (Nottale, 1998, p. 89).
Avant Albert Einstein, l'espace et le temps sont donc deux espaces distincts : l'un à trois dimensions, l'autre à une dimension. Après Albert Einstein (1956 ; 1990), il n'y a plus qu'un espace-temps à quatre dimensions plat (espace-temps quotidien) ou courbe (espace-temps einsteinien). Avec Laurent Nottale, on essaye de définir une relativité d'échelle, c'est-à-dire une cinquième dimension expliquant la fractalité des objets.
Cela étant, le principe de relativité pose que les lois fondamentales de la nature sont uniques et qu'elles s'appliquent dans tous les cas et dans toutes les situations. « Ce qu'il exprime, c'est que le monde est un » (Nottale, 1998, p. 94). En liant deux à deux des entités il établit une cohérence et une unité du monde.
Toutefois, il ne faut pas confondre relativisme et relativité. Le relativisme est un cliché posé par la postmodernité qui consiste à dire que tout est relatif. Par contre, « ce qu'affirme le principe de relativité, c'est qu'il existe certaines grandeurs particulières, caractérisant l'état du système de coordonnées, grandeurs qui ne peuvent jamais être définies de manière absolue. En un sens plus général encore, on peut dire que ces grandeurs réalisent l'interface entre nous et le monde extérieur, sur lequel nous voulons effectuer des mesures » (Nottale, 1998, p. 103). « La relativité consiste en fait en une recherche de l'universel à travers une analyse du relatif » (Nottale, 1998, p. 104).
4.1.2.2. Les principes mathématiques
Selon Blaise Pascal dans De l'Esprit de la géométrie, c'était la géométrie qui devait être le support des mathématiques. Il reprenait l'idée de Galilée selon laquelle le monde « est écrit dans le langage des mathématiques ».
Depuis les choses ont un peu changé, le support des mathématiques est devenu la théorie des ensembles, et non plus la géométrie. En effet, s'il y avait une théorie mathématique que le néophyte devrait chercher à comprendre, sans nul doute, il faudrait que ce soit la théorie des ensembles, ou plus généralement la théorie axiomatique sur laquelle repose toutes les mathématiques modernes.
C'est Georg Cantor qui en a posé les jalons. Après bien des querelles, ce fut finalement la théorie de Zermelo-Fraenkel (ZF) qui fut retenue comme base axiomatique de la théorie des mathématiques. Par la suite, Kurt Gödel et Paul Cohen, deux logiciens, vont définir les modèles de la théorie des ensembles. Ces modèles sont nécessaires car ils permettront de cadrer les futures théories géographiques. « A cause du théorème d'incomplétude de Kurt Gödel, il faut abandonner tout espoir de montrer que la théorie des ensembles ne comporte pas de contradiction » (Krivine, 1988, p. 1). Cela signifie qu'une théorie géographique fondée sur des démonstrations mathématiques sera valable dans la limite du modèle ensembliste sur lequel elle est construite.
4.1.2.2.1. La théorie des ensembles ZF
On appelle la théorie des ensembles ZF (Zermelo-Fraenkel) les cinq axiomes suivants :
l'axiome d'extensionalité ;
'axiome de la somme (ou de la réunion) ;
l'axiome de l'ensemble des parties ;
le schéma d'axiomes de substitution (ou de remplacement) ;
l'axiome de l'infini.
Généralement, on y ajoute l'axiome du choix. La théorie ZF devient alors la théorie ZFC qui est le modèle ensembliste le plus courant. Pour le détail de ces axiomes, il nous faut renvoyer à la bibliographie (Krivine, 1988 ; Gauthier, 1997).
Les axiomes de la théorie des ensembles expriment, en fait, les propriétés que l'on impose à la relation binaire « appartient à » considérée.
4.1.2.2.2. Les principes admis, mais discutables
Les concepts de quantité et de qualité sont essentiels. En mathématique, on utilise les deux, même si le concept de quantité l'emporte. On trouve des théories qualitatives en topologie, par exemple, d'où découle la théorie des graphes. Quant à la quantité, elle est liée à la théorie de la mesure qui permet de compter les choses.
A cela s'ajoute l'hypothèse de la continuité qui est lourde de conséquences en mathématique. La continuité est privilégiée par rapport à la discontinuité car elle est plus simple à mettre en œuvre. Par exemple, toute la théorie des équations différentielles repose sur elle. Toutefois, comme l'écrivait René Thom (1991), il existe deux manières de voir un segment : il s'agit soit d'un nombre infini de points côte à côte, soit d'un trait.
4.1.3. L'intuition de l'espace et du temps
Pour mesurer cette intuition d'après Emmanuel Kant, il nous faut un référentiel c'est-à-dire une origine par rapport à laquelle nous allons définir la notion de distance dans l'espace, celle de durée dans le temps et celle de temps propre dans un espace-temps qui correspond à l'horloge interne d'un système donné.
4.1.3.1. L'espace
Le concept d'espace est aussi flou que celui du temps. Qu'est-ce que l'espace ? A une telle question, le bon sens répondrait par un gallicisme : « L'espace, c'est… ». En réalité, il n'en est rien. Etymologiquement, le terme spaze apparaît au XIIe siècle avec la signification de « moment ». Jusqu'au XVIe siècle, il avait le « sens d'espace-temps ». La modernité va séparer l'espace du temps, et mettre ce dernier en avant. Le temps est lié à une cause efficiente. « La nature de l'espace est énigmatique parce qu'il semble d'une part être pour les choses étendues l'extension même qui fait qu'elles sont, mais parce qu'il semble aussi être un lieu vide dans lequel on peut mettre les choses étendues » (Bachelet, 1999, p. 3). Il existe deux conceptions de l'espace : « l'espace désigne une qualité topologique du monde des objets matériels » (Bachelet, 1999, p. 3) et « l'espace est le réceptacle de tous les objets matériels » (Bachelet, 1999, p.3). Dans la première conception, « on ne peut concevoir d'espace sans objet matériel » (Bachelet, 1999, p. 3). Dans la seconde conception, « un objet matériel ne peut être conçu qu'en tant qu'il existe dans l'espace » (Bachelet, 1999). Autrement dit, « l'espace apparaît alors comme une réalité qui en quelque sorte transcende le monde matériel » (Bachelet, 1999, p. 3). Cette citation montre la complexité à définir ce qu'est un espace. Il est soit abstrait, soit tangible, avec ou sans limites. En conclusion, « le concept d'espace doit être conçu dans la multiplicité si et dans la mesure où, dans un espace, on peut en mettre un autre qui ne se confond pas avec le premier parce qu'il en diffère par un ou plusieurs propriétés » (Bachelet, 1999, p. 3).
Si on fait le point sur quelques définitions trouvées dans Le Robert (1970), dans la Focus encyclopédie (1972) et dans le Petit Larousse en couleur (1989), on se rend facilement compte que le terme « espace » est très ambigu, polysémique. Sa définition est très vague. La situation de l'espace est historiquement plus problématique que celle du temps, puisque le terme a de toute époque été compris comme ayant plusieurs dimensions, alors que la complexité du temps n'a été découverte qu'à la fin du XXe siècle, au début du XXIe siècle ! Toutefois, deux notions apparaissent. Ce sont celle de l'« étendue » et celle de l'« infini ». L'infinitude de l'espace suppose que l'espace peut être non délimité. L'espace est une étendue infinie, et le Larousse ajoute, « qui contient et entoure tous les objets. » Cependant, même si l'espace est infini, on peut toujours travailler sur une portion d'espace, qui est une « étendue limitée à un certain nombre de dimensions », dans laquelle on peut mesurer « ce qui sépare deux points, deux lignes, deux objets. » Cette mesure nécessite une géométrie qui introduit une métrique et la notion de distance, qui permettent d'évaluer un écartement entre deux points, ce qui montre toute l'ambiguïté du terme, puisque cette définition peut correspondre à un intervalle de temps. L'espace peut être une « étendue dans le temps », ce qui est nécessaire, sinon on ne pourrait pas mesurer le temps. D'où l'idée de préciser la définition du terme soit par un épithète, soit par un complément du nom. Ainsi, chaque discipline a pu définir son espace. Surmontant ainsi la difficulté lexicologique du terme « espace », mais cette notion, comme celle de temps, est toujours controversée aujourd'hui. Peut-on avec l'avancée scientifique actuelle proposer une définition du terme en lui-même .
On peut diviser les espaces en trois classes : les espaces mathématiques (abstraits, construits, objectifs) que l'on peut établir avec des règles (axiomes et théorèmes), les espaces tangibles, matériels, explorés et explorables et les espaces psychologiques. Le premier est un ensemble de points muni d'une structure, le second et le troisième sont des expressions, des manifestations de cette étendue, c'est-à-dire de ce que nos sens en connaissent.
Nous allons nous intéresser plus particulièrement aux espaces mathématiques. Parmi eux, il y a d'abord les espaces vectoriels qui possèdent une infinité de dimensions entières, dans lesquels s'appliquent des mesures. Le deuxième type est celui de l'espace topologique qui ne possède pas de métrique, mais établit un rapport de position relative entre les différents points des structures composant cet espace. Pour Henri Poincaré, l'espace est forcément géométrique. Ce type d'espace a cinq propriétés. « Il est continu. Il est infini. Il a trois dimensions. Il est homogène, c'est-à-dire que tous ses points sont identiques entre eux. Il est isotrope, c'est-à-dire que toutes les droites qui passent par un même point sont identiques entre elles. ».
Cet espace mathématique permet de définition la position d'un point par rapport à un référentiel auquel il est lié. Celui du référentiel (R) est l'association :
(1) d'un point O invariant appelé origine ;
(2) d'une base formée de n vecteurs fixes dans (R).
Par défaut, l'espace désignera toujours un espace euclidien à trois dimensions (i, j, k). Au-delà, on parlera d'hyperespace comme l'espace-temps. Cet espace possède quatre dimensions. Il a été inventé par Albert Einstein lorsqu'il a résolu les équations de la relativité générale. Il crée un espace-temps, renouant ainsi avec le sens étymologique du terme « espace ». Aujourd'hui, avec Laurent Nottale (1998 ; 2000), on arrive à un espace-temps fractal, c'est-à-dire un espace à cinq dimensions, la cinquième correspondant à la dimension fractale (variable).
L'espace est infini par définition. Il existe deux manières complémentaires de définir mathématiquement l'espace : par les distances et par les angles.
4.1.3.2. Le temps
Le temps est un concept polysémique. Chacun cherche à définir le temps, et ce depuis la Haute Antiquité, mais il est instable, éphémère alors comment le définir ? Généralement, on cherche d'abord à le mesurer. Ainsi, partout sur la terre, les hommes ont cherché tous les moyens pour réussir à mesurer de la manière la plus précise possible quelque chose qu'ils ressentaient. Pourquoi cette quête s'est-elle poursuivie de tout temps et en tout lieu ? Tout simplement parce que le temps est lié à l'existence de l'homme. On vit dans le temps et grâce au temps. Quand il s'arrête, c'est que l'être est mort. La définition du terme est aujourd'hui toujours vague. Toutefois à partir des connaissances techniques de notre civilisation certaines « réponses » ont été trouvées. Le temps est-il oxymore ? Il est « évident et impalpable », « substantiel et fuyant » et « familier et mystérieux » (Klein, 1995, p. 9-10), continu et discontinu, linéaire et cyclique. Krzysztof Pomian souligne, lui, que « le temps est lui-même un objet temporel » (Pomian, 1984, p. XIV). Comment alors mettre de l'ordre dans le temps ? « Le temps risque toujours d'être identifié aux phénomènes qu'il contient. Or ce qui s'écoule dans le temps n'est pas la même chose que le temps lui-même » (Klein, 2004, p. 16). « Le temps est consubstantiel au monde : rien ne peut advenir ni persister en dehors de lui » (Klein, 2004, p. 47-48).
Le repérage et la mesure dans le temps sont plus difficiles à définir que pour l'espace. Il est constitué par l'association :
(1) d'un instant d'origine (t0) ;
(2) d'une unité de durée associée à un compteur de temps.
L'instant correspond à une « position » dans le temps. La durée est la mesure d'un intervalle de temps séparant le début et la fin d'un événement tn. La date est une durée qui sépare l'instant d'origine à l'instant de fin tn.
L'instant possède un début et une fin. Il est toujours borné. Sa seule représentation est réalisée par une géométrie (droite pour les phénomènes linéaires, cercle pour les phénomènes cycliques). La question du temps peut être abordée de deux façons : soit au travers d'une perception, soit en fonction d'une rationalisation. La perception est à la base de l'a priori kantien. Elle conduit à l'idée de déroulement, d'évolution, de sens ou de flèche du temps ; autant de choses qui restent encore largement subjectives. La géométrisation du temps est à la base de sa rationalisation à partir d'une norme (la seconde par exemple), d'un point initial (la naissance de Jésus Christ par exemple) et d'une structure topologique ordonnée (avant → après, t1 → t2 → tn) que l'on rapproche d'une structure causale (cause → conséquence) depuis Guillaume d'Ockham (vers 1280 – vers 1348). C'est ainsi que l'on peut évoquer le paradoxe de Stephen Hawking au sujet des rapports entre le temps et l'espace. En effet, « Le temps ne serait en quelque sorte qu'un accident de l'espace » (Prigogine, 1996, p. 23-24), mais « nous avons besoin d'une flèche du temps pour rendre compte de la vie intelligente » (Prigogine, 1996, p. 24).
4.1.3.3. L'espace-temps
La théorie restreinte d'Albert Einstein (1905) montre que l'espace et le temps ne sont pas distincts d'un point de vue de leurs coordonnées. Autrement dit, l'espace dans lequel nous vivons est un espace à quatre dimensions dans lequel nos sens ne peuvent en percevoir que deux, et où la troisième n'est qu'une mise en perspective réalisée par l'intermédiaire de notre cerveau.
4.1.3.4. Les sept symétries de l'espace-temps (ou principe de Noether ou théorème de Noether)
Les sept symétries de l'espace-temps ont été formulées par Emmy Noether en 1915. En géométrie, il s'agit d'une « transformation qui ne change ni la forme, ni les dimensions d'une figure ».
La symétrie de translation dans l'espace correspond à la conservation de l'impulsion (quantité de mouvement).
La symétrie de translation dans le temps correspond à la conservation de l'énergie.
La symétrie de rotation dans l'espace correspond à la conservation du moment cinétique (angle).
La formulation de ces sept symétries signifie que le temps et l'espace sont homogènes : il n'y a pas d'origine. De plus, il n'y a pas de direction privilégiée : l'espace est isotrope. Il est bon de rappeler ces quelques définitions élémentaires car, en relativité d'échelle, on va retrouver ces quantités dans l'espace des échelles.
4.1.3.4.1. L'impulsion
L'impulsion est une grandeur vectorielle à trois composantes. Il s'agit de la quantité conservée par rapport à l'espace lors d'un déplacement. D'après la loi de Newton,
![]()
c'est-à-dire
![]()
on appelle cette quantité impulsion qui est formulée soit par ![]() .
.
Elle correspond donc au produit de la force par l'intervalle de temps pendant lequel elle agit. Autrement, pendant un intervalle de temps infinitésimal dt, l'impulsion élémentaire d'une force F est le vecteur Fdt. Entre deux instants t1 et t2, l'impulsion totale est la somme des impulsions élémentaires.
![]()
donc
![]()
or le produit ![]()
![]() est appelé le moment d'une force.
est appelé le moment d'une force.
La force peut donc se définir comme la dérivée de l'impulsion par rapport au temps. En effet, on sait que :
![]()
donc
![]() .
.
4.1.3.4.2. L'énergie
L'énergie est une grandeur scalaire. Il s'agit de la quantité conservée dans le temps. D'après les physiciens, l'énergie interne E ou la masse M de tout système isolé ou inertiel ne varient pas en fonction du temps s'il n'y a pas d'apport ou de retrait d'énergie (ou de masse) ou de chaleur de l'extérieur de ce système. Mathématiquement, cet énoncé s'énonce ainsi :
![]() .
.
C'est le principe de conservation de l'énergie que l'on peut écrire sous forme d'une équation différentielle :
![]() = 0.
= 0.
Soient un déplacement élémentaire dM, le travail d'une force dW et la force F, on définit :
![]() .
.
Par contre, le potentiel énergétique φ se calcule par rapport à l'espace. On dit qu'une force F dérive d'une énergie potentielle s'il existe une fonction ψ telle que :
![]()
![]() est le vecteur gradient.
est le vecteur gradient.
Pour tout déplacement infinitésimal dM, on a :
![]() .
.
La variation de l'énergie potentielle est égale au travail effectué par une force - F qui équilibre à chaque instant F, pour amener l'objet déplacé d'une origine arbitraire O au point M. Cette énergie est potentiellement disponible en M : il suffirait de laisser la particule revenir en O pour récupérer la même quantité d'énergie ψ(M).
Enfin, il faut retenir que la dérivée du potentiel ψ par rapport à la position x donne la force.
![]() .
.
4.1.3.4.3. Le moment angulaire
Le moment angulaire est une grandeur vectorielle à trois composantes. Il symbolise la conservation des angles. Il possède la même définition que le moment d'une force lors d'un déplacement, sauf qu'au lieu d'avoir une distance, on a un angle.
![]()
Cet angle φ définit ce que l'on appelle l'orientation dans un espace à trois dimensions. Le moment angulaire possède grosso modo les mêmes propriétés que l'impulsion.
4.1.3.4.4. Le principe de Curie
Un principe pratique sur les symétries a été formulé par Pierre Curie. « Si une cause présente une certaine symétrie ou invariance, alors son effet aura la même symétrie, à condition que la solution du problème soit unique ». Les éléments de symétrie agissent sur les directions des grandes vectorielles, tandis que les invariances agissent sur les variables dont dépendent ces grandeurs.
4.1.3.5. L'échelle
Entre donc en ligne de compte un autre phénomène que connaissent bien les géographes. C'est celui de l'échelle. Classiquement, en géographie, on considéra qu'à certaines échelles, c'est-à-dire en fonction de certaines tailles, de certains niveaux, se structurent des cohérences, voire des formes, qui peuvent ensuite être mises en relation avec d'autres entités d'échelle différente, plus grande et dans ce cas la seconde organisation est emboîtée dans la première, ou plus petite et dans ce cas la première est englobée par celle plus vaste développée à petite échelle (Forriez, Martin, 2006).
Tout objet géographique est donc forcément encadré par deux échelles : une échelle inférieure à partir de laquelle l'objet n'est plus observable et une échelle supérieure à partir de laquelle l'objet se dilue dans un espace plus vaste. L'échelle entendue comme rapport de taille permet donc d'articuler une discontinuité fondamentale dans le sens où elle fixe une condition d'existence de l'objet géographique étudié. Cette condition d'existence est liée à sa cohérence.
Il est possible d'aller au-delà de ces relations d'emboîtement et d'englobement qui mettent en jeu des états fixes et des rapports entre états fixes en introduisant la logique de la dimension fractale. Celle-ci est bien connue maintenant (Martin, 2003, 2004, 2005, 2006). Elle consiste à porter une attention aux rapports entre échelles et à établir un formalisme qui rende compte de la façon dont le développement dans l'ordre des échelles se réalise. Les dimensions fractales, « plurifractales » ou multifractales en rendent compte.
On voit donc bien ici que la réflexion géographique et que la pratique des géographes auraient pu être considérées comme une première approche de ces questions. Il n'en est rien, semble-t-il, mais cela n'implique pas moins que la culture géographique prépare d'une certaine façon à une pensée qui met en œuvre une logique fractale. Certes il est clair que certains formalismes qui la caractérisent sont difficiles à maîtriser pour qui n'est pas mathématicien mais cela n'exclut en rien que soient intégrées, dans la culture géographique, les idées essentielles que véhicule cette forme de pensée. C'est ce à quoi nous nous essayerons ici en limitant autant que faire se peut le recours à tel ou tel formalisme.
Dans une fractale déterministe, le développement dans l'ordre des échelles est infini que ce soit vers les petites ou vers les grandes échelles. Dans la nature, les constructions s'affrontent à la matérialité du monde et le développement dans l'ordre des échelles est limité à une gamme d'échelles particulière par ce que l'on nomme généralement des échelles de coupure (Martin, 2005) qui sont d'une part en relation avec les limites des objets, et d'autre part avec les délimitations de champs académiques. Ainsi à une certaine grande échelle, celle du cristal, passe-t-on de la géomorphologie à la cristallographie. De même pour une échelle très petite passe-t-on de la géographie qui a comme objet d'étude l'interface terrestre, à la cosmologie qui traite semble-t-il de bien des mondes étranges.
Localement, les objets qui ont été déployés selon ce principe récursif fractal sont des objets d'échelle. Il faut bien voir qu'ils sont définis par une structure dont l'idée sous-jacente est simple (rapports entre les échelles) alors qu'ils se donnent à voir comme des objets complexes ou compliqués. Complexes parce qu'ils exhibent des propriétés particulières (non dérivabilité par exemple) ; compliqués parce que les décrire au moyen de mots nous conduit inexorablement à des formulations poétiques, à des images, à des oxymores. Cela étant, les objets fractals sont totalement ubiquistes et la logique fractale est universelle.
La théorie de la relativité d'échelle permet d'identifier cet ordre scalaire comme étant mathématique, ou plus exactement géométrique. Autrement dit, les discontinuités inférieure et supérieure ne sont pas dues au seul hasard. Il existe bien une partition déterminée et déterminable. C'est pour cela que doit être mis en place le concept d'espace fractal, remplaçant celui d'objet fractal. On verra par la suite que l'échelle va devenir avec la théorie de la relativité d'échelle une variable primaire au même titre que l'espace et le temps.
4.1.3.6. Conclusion partielle
Au final, nous pourrions faire remarquer que toutes les notions liées au temps, à l'espace et aux échelles sont définies de manière suffisamment générale pour être reprises telles quelles en géographie. Aussi, est-il besoin de les transposer dans notre discipline ? La question est posée.
Cependant, d'un point de vue méthodologique, j'ai choisi de ne pas modifier ces définitions dans un premier temps. Par contre, toutes les autres grandeurs sont des constructions mathématiques permettant de résoudre des problèmes dans une science spécifique. L'archétype est la notion de masse, ou encore celle de force. Ainsi, les masses, les trajectoires, les dynamiques, etc. sont des grandeurs physiques qui, à la différence de la position, de l'orientation, de l'instant, de l'impulsion, du moment angulaire et de l'énergie, devront être adaptées en géographie afin d'y prendre un sens géographique.
L'espace | Le temps | L'espace-temps | ||
|---|---|---|---|---|
Distance | Angle | |||
La grandeur primaire | Position | Orientation | Instant | Temps propre |
La grandeur conservative associée | Impulsion | Moment angulaire | Energie | Impulsion |
Les types de variables | Vecteur5 | Vecteur | Scalaire | Quadrivecteur6 |
Pour ne pas brûler les étapes, ce tableau sera légèrement complexifié à la fin de la seconde partie en introduisant la notion d'échelle.
4.2. La position de la géographie
4.2.1. La définition de la science géographique
La géographie, rappelons-le, a pour projet d'expliquer les morphologies déployées sur l'interface terrestre et celles produites par celui-ci (Dauphiné, 2003, p. 148 ; Martin, 2004b, p. 23). Par définition, ce projet la fait correspondre à une science spatiale. Autrement dit, le projet de la géographie est d'étudier les propriétés d'un espace relatif et les processus qui contribuent à différencier les lieux. Dans ces processus, il y a autant ce qui est de l'ordre de la représentation que ce qui de l'ordre culturel, ce qui est de l'ordre du physique, le topos, et ce qui est de l'ordre anthropologique ou sociétal. C'est donc l'étude de la mobilité de (et sur) l'interface terrestre.
Selon Paul Ricœur (2000), la géographie doit mettre de l'ordre dans l'espace. Qu'est-ce que l'espace géographique ? Depuis la naissance du courant de l'analyse spatiale dans les années 1960, la question est restée polémique. L'adaptation de certaines lois de la physique à l'espace géographique pose problème car il n'y a pas de compréhension profonde des principes dont elles découlent. Ainsi, dans de nombreux cas, cela aboutit à des problèmes conceptuels importants, voire à des contradictions par rapport au projet de la géographie.
Pourquoi la géographie a-t-elle besoin d'une définition spatiale ? Tout simplement parce que, dès ses origines les plus lointaines, la géographie s'est intéressée au rôle de la distance entre de deux objets géographiques. Cependant, Paul Claval (2003) rappelle que plus on avance dans le temps, plus le rôle de la distance devient complexe.
Un objet géographique est une forme localisée dans l'espace géographique, c'est-à-dire sur l'interface terrestre. Cette forme possède une localisation précise, une matérialité, un champ et une dynamique. Cette forme a deux origines : soit elle a été créée par l'homme, soit elle est d'origine naturelle. Elle se déploie généralement dans un espace à cinq dimensions : la longueur, la largeur, la hauteur, le temps et l'échelle. L'échelle doit être pris ici au sens de « résolution », de taille, de rapport de tailles. De ce fait, la géographie est-elle la science des structures spatiales ? La géographie possède-t-elle des lois spatiales .
La géographie répond à quatre questions. Où sont les choses ? Comment les structures spatiales se sont-elles générées ? (Le « comment où » ?) Quels sont les rapports de positions ? (Le « pourquoi où ? ») Peut-on instrumentaliser les formes spatiales ? (Le « à quoi sert la géographie ? ») L'un des problèmes est que la géographie ne possède pas de théorie de la forme, c'est-à-dire de théories expliquant la formation des discontinuités spatiales.
4.2.1.1. Le champ phénoménal
La géographie signifie « description de la terre ». Selon la nature des phénomènes, on distingue la géographie physique, la biogéographie et l'anthropogéographie. La géographie physique regroupe la géodynamique, la géomorphologie, la climatologie, la météorologie, l'océanographie, l'hydrographie et la glaciologie. L'anthropogéographie est composée de la géographie humaine, la géographie historique, la géopolitique, la géographie sociale et la géographie économique. La géographie étudie la répartition de certains phénomènes à la surface de la terre et des causes de cette répartition. La méthode utilisée par les géographes a très tôt été celle de la systémique.
4.2.1.2. Le champ théorique
Comme toutes les sciences humaines, il est très pauvre.>
4.2.1.3. Le champ ontologique
Son champ ontologique concerne aussi la réalité de la perception que les hommes ont de leur espace. La géographie semble aujourd'hui développer à deux champs d'investigation : un champ phénoménologique, qui prône une analyse sociale, et un champ mathématique, qui prône une analyse spatiale. Les deux approches sont complémentaires, en même temps elles s'opposent. Elles sont donc ago-antagonistes. En cela, la géographie tend à être plus en accord avec une pensée qui cherche à dépasser la modernité, avec une pensée transmoderne. C'est peut être ce qui lui conférera demain son utilité sociale.
4.2.2. Les principes géographiques
Il s'agit ici de proposer quelques éléments de définition des principes premiers qui seraient spécifiques à une démarche géographique, et de relancer un vieux débat soulevé au Géopoint de 1980. Les principes géographiques ne sont pas aussi affirmés que ceux de la physique. Aussi, il faut formuler les principes géographiques sous forme de questions qui doivent être résolues avant de traiter un problème géographique. La recherche de principes géographiques est de passer de la question « comment où ? » à « pourquoi où ? ». De plus, cela permettrait de résoudre partiellement le problème de l'idéologie qu'il peut y avoir derrière la quantification. La mathématisation de ces principes permettrait de faire progresser la conceptualisation de la géographie car l'invention de nouvelles structures mathématiques modifiera les théories géographiques (fig. 8).
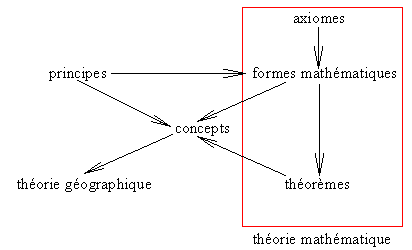
4.2.2.1. Le principe de continuité et finitude
L'interface terrestre est-elle continue ou discontinue ? Est-elle finie ou infinie ? La réponse à ces questions reste difficile. C'est plus une question de choix méthodologique.
Traditionnellement, l'analyse spatiale présente l'interface terrestre comme étant infinie. De plus, l'espace est discontinu. Une discontinuité est une rupture apparaissant dans l'espace ou dans le temps. L'espace est riche en discontinuités de toutes sortes, marquées par des interfaces, des limites et des frontières. Les discontinuités peuvent être : (1) franches, brutales (une frontière, un mur…) ou (2) progressives, ménagées (une transition, une marge, une marche, une plage. Il existe deux types de discontinuités : les discontinuités exogènes, provoquées de l'extérieur et les discontinuités endogènes, produites par le processus lui-même, par le fonctionnement du système, sans intervention directe de l'environnement. Dans de nombreux cas, les discontinuités apparaissent dans l'étagement des phénomènes géographiques en altitude. La discontinuité endogène rétablit une forme de continuité là où l'on voit souvent une rupture inexplicable ou jugée exogène. D'après Roger Brunet, l'espace géographique comporte quatre grandes sortes de discontinuités : (1) toutes celles qui sont associées à l'approximation, aux maillages ; (2) toutes celles qui résultent du jeu des principales lois de l'espace ; (3) toutes les lignes de contact (ou interface) ; (4) toutes les limites de contrées qui marquent le passage d'un système spatial à un autre.
Toutefois, on se rend bien compte aujourd'hui que l'interface terrestre est finie. C'est une évidence géométriquement. La terre présente une surface « sphérique ». Cependant, paradoxalement, l'homme ressent cet espace géographique de manière infinie, or l'interface terrestre n'est qu'une bande coincée entre le manteau et l'atmosphère. Elle reste un espace continu. Cependant, bien qu'ayant cette qualité, elle est partitionnée par des discontinuités anthropiques et physiques. Comment émergent de telles discontinuités ? Les processus spatiaux ont toujours été envisagés de manière purement descriptive soit par des modèles discursifs soit par des modèles mathématiques. Pour ces derniers, il n'y a jamais eu réellement d'analyse, au sens mathématique terme. Pourquoi ? La réponse est simple : aucun outil ne permet de quantifier et d'analyser ces processus spatiaux. Nous verrons par la suite qu'un espoir nous est permis grâce à l'analyse fractale7 qui tentera de montrer que la discontinuité émerge du continu.
Enfin, si la Terre présente une surface finie face à laquelle les Hommes ne peuvent rien, sauf s'ils parviennent, un jour, à organiser des voyages interplanétaires ou intergalactiques. Les fronts pionniers vont donc disparaître. Nous sommes alors dans une logique complètement paradoxale d'infinité reposant sur la surface, alors que, manifestement, nous sommes en réalité dans une logique finie. Dès lors, comment organiser autrement la Terre ? Il n'y a plus qu'une seule solution : c'est conquérir l'espace des échelles (terrestres) qui lui est réellement infini, dans la mesure où l'on pourra toujours créer un niveau intermédiaire plus ou moins pertinent. Il faut souligner que la géographie a tout de même été pionnière dans les raisonnements d'emboîtement d'échelles et d'effets d'échelle. Elle a montré que la seule manière d'organiser les territoires, au sens très large du terme, à l'heure actuelle était de favoriser le partenariat des différents acteurs qui interviennent à différentes échelles. Autrement dit, un nouveau « front pionnier » se met en marche : la conquête, ou plus précisément, la maîtrise des échelles.
Cependant, la conquête des échelles ne concerne plus l'unique géographie. La découverte des fractales a ouvert un important champ transdisciplinaire qui montre que tous les phénomènes naturels et/ou anthropiques prennent des formes fractales issues de dynamiques chaotiques, qui ont été démontrées par Laurent Nottale comme étant inévitables. Même si ces courants tendent à s'essouffler aujourd'hui, il n'en reste pas moins qu'ils ont mis en évidence toute sorte des règles d'échelle. Ce mémoire se propose d'aller au-delà de ces approches à la lumière de la relativité d'échelle de Laurent Nottale.
Pour conclure, l'Humanité, si elle veut survivre, n'aura pas d'autres choix que de se partager les maigres ressources de notre planète, mais aussi, de commencer à apprendre à vivre avec la Nature, surtout dans les sociétés occidentales. Celles-ci ont dès lors une énorme responsabilité : il faut qu'elles admettent que le modèle tant admiré par de nombreux pays en voie de développement, est le pire qui soit pour l'avenir de l'espèce humaine. En effet, certains spécialistes avancent l'idée que si la planète entière vivait en suivant les mêmes uses et coutumes que l'Occident, il faudrait deux ou trois planètes pour survenir à la demande globale. Il est donc urgent de modifier notre approche de la gestion des territoires. Le géographe deviendrait alors le porte-parole et le chercheur par excellence de cette nouvelle philosophie du monde, surtout à l'heure de la mondialisation. Définir un principe de continuité et d'infinitude serait donc le bien venu en géographie.
4.2.2.2. Le principe d'anisotropie et d'hétérogénéité
Il s'agit de notions mathématiques précises. Isotrope signifie que toutes les directions sont équivalentes. L'espace isotrope est un espace idéal, non dissymétrique, non orienté, non différencié, qui est parfois introduit dans la réflexion théorique des économistes. A contrario, anisotrope signifie que toutes les directions ne se « valent » pas. La géographie est contrainte de poser au départ l'anisotropie de son espace, même dans la modélisation.
Homogène signifie de même origine. Un espace homogène est défini par des parties qui se ressemblent, ou forment un tout, quelles que soient leurs origines. Par contre, hétérogène signifie qui a une autre nature. L'espace hétérogène désigne ce qui fait de parties de nature différente et peu liée, ce qui manque d'unité. Le choix est plus délicat.
Toutefois, en géographie, on étudie les deux. Par exemple, pour les automates cellulaires ou pour les systèmes multi-agents, l'espace de départ est isotrope et homogène. Puis, progressivement, il devient anisotrope et hétérogène. Un problème épistémologique se pose alors sur l'origine de cette anisotropie de l'espace géographique : soit, au départ, il était isotrope et homogène, soit il était anisotrope et homogène dès le début (ce qui est peu probable, mais reste possible).
Aussi, il est difficile d'ériger en principe géographique les notions de continuité-discontinuité, de finitude-infinitude, d'isotropie-anisotropie et d'homogénéité-hétérogénéité. Il nous faut, comme la physique, étudier l'espace géographique à la lumière des couples possibles.
4.2.2.3. Le principe d'interaction (ou des actions réciproques)
Le mouvement est une variation au cours du temps de la position. Il s'oppose au terme statique qui désigne les positions fixes. La mesure du mouvement s'effectue par la vitesse, elle-même mesurée par l'accélération. A contrario, en géographie, la position des lieux est « fixe », mais le temps s'écoule, à quelques exceptions près comme la dérive des continent ou l'abandon d'un lieu par l'homme.
A l'origine, la dynamique désigne la physique des forces et des accélérations. Elle se décompose en deux : la cinématique qui étudie le mouvement et la statique qui étudie immobilisme. Le but des lois de la dynamique est de déduire le mouvement des corps à partir de la connaissance des forces s'exerçant sur eux et des conditions initiales du mouvement. La dynamique part de l'axiome suivant : tout changement de lieu se produit uniquement dans le temps. Autrement dit, tout mouvement est un changement continu de lieu auquel correspond des valeurs du temps variant d'une manière continue. Les trois lois de la dynamique ont été formulées par Isaac Newton. La première loi d'Isaac Newton énonce le principe de l'inertie. La seconde loi d'Isaac Newton précise que, dans un référentiel galiléen, la somme des forces extérieures8 est égale à l'accélération pondérée par la masse.
L'action se définit par le fait que des objets exercent des forces les unes sur les autres, et les forces sont des causes de déformation, de mouvement ou de propagation. A contrario, L'interaction se définit par des actions réciproques. L'interaction s'exerce soit par un contact direct, soit à distance. Si deux corps A et B sont en contact, l'action de A sur B s'accompagne toujours de l'action de B sur A que les corps soient immobiles ou en mouvement. Autrement dit, mathématiquement, lorsqu'un corps A exerce sur un corps B une force F de A sur B, le corps B exerce une force F de B sur A telle que FA→B = –FB→A.
Ce principe a été importé en géographie par Peter Haggett (1973) pour étudier l'interaction spatiale entre deux lieux, sans toutefois définir ce qu'était un lieu ! Le principe d'interaction permet d'étudier l'arrangement entre les lieux.
4.2.3. L'espace géographique
L'espace est un concept flou. Si nous partons du principe qu'il existe un espace géographique, comment le définir ? Quel est son intérêt ? Il est amusant de constater que la géographie, aujourd'hui, articule le concept d'« espace » avec celui de « territoire », ce dernier terme étant défini par le premier. En effet, un territoire est un espace non approprié. Cependant, avec cette approche, le problème reste entier. Que signifie le mot « espace » ? On ne le sait pas. L'unique certitude est qu'un espace n'est pas un territoire. La deuxième solution qu'a proposée la géographe a été d'expliquer le terme « espace » par un épithète ou un complément du nom, ajouté à celui-ci. La difficulté lexicologique est une nouvelle fois contournée par un stratagème. Cependant, toutes les autres disciplines possédant un aspect spatial, ont fait de même. Ainsi, bien que, devenue science de l'espace dans les années 1960, la géographie n'a jamais défini clairement son concept fondamental.
L'espace permet d'éclaircir la notion d'espacement, à travers le concept de distance qui en est sa mesure. L'espace, dans cette perspective, est purement géométrique. C'est aussi l'espace matériel. Enfin, l'espace est une étendue sur laquelle se déploient des phénomènes. Il est donc cartographiable, d'ailleurs représenté comme tel dès la Renaissance ! On constate que trois éléments sont toujours présents dans l'espace : la surface, la droite, le point, même si, depuis peu, on essaye d'y introduire le volume comme avec des modèles numériques de terrain. Cependant, c'est par la combinaison de ces éléments que résultent les images de l'espace. Toutefois, l'espace n'est pas l'espace géographique. L'espace géographique renvoie à une approche sociale et spatiale de l'espace. Il permet de comprendre les répartitions (ou les organisations) spatiales. On voit tout de suite que l'idée d'espace géographique s'oppose à l'idée d'étendue car c'est bien la société qui, en fonction de ses projets et de ses possibilités techniques, transforme de l'étendue (espace) en espace géographique. L'espace géographique est un tout complexe formé à la fois d'éléments visibles comme les lieux, les réseaux et les espacements, et d'éléments invisibles comme tout ce qui est social. Cependant, l'espace géographique n'est pas un ensemble de lieux. C'est une somme de connexion entre les lieux. Autrement dit, ce sont les interrelations entre les lieux qui constituent la structure de l'espace géographique.
L'analyse spatiale est l'école de la géographie qui essaye de comprendre ces interrelations en essayant de les modéliser par des lois. Cette proposition revient à dire que la position dans l'espace n'est pas neutre. En effet, il existe deux lectures de l'espace géographique : l'espace support et l'espace acteur. L'espace support est l'espace des structures et des organisations spatiales, tandis que l'espace acteur est l'espace des relations entre les lieux et des ensembles de lieux. À travers l'analyse spatiale, on recherche une méthode et une formalisation de la géographie.
La figure 9 montre que le rapport entre l'espace et la société est double. (1) L'espace permet de dégager des régularités et des lois spatiales contraignant la société. (2) La société permet de dégager les attributs contraignant l'espace. L'espace géographique serait donc un potentiel que les acteurs et agents réexaminent et réévaluent continuellement en fonction de leurs besoins et leurs aspirations.
La localisation est toujours le point de départ de toute étude géographique. Un objet géographique est localisé sur l'interface terrestre. On peut alors définir l'espace comme étant une somme de lieux. Ces lieux sont plus ou moins bien connectés entre eux par des voies de communication de nature différente. Ils peuvent être terrestres, aériens, aquatiques, subaquatiques ou virtuels… Ces chemins d'accès matérialisent une forme que l'on appelle réseau. Les lieux peuvent être considérés comme des variables ou des invariants grâce à leur position relative. Une dynamique propre à ces différents lieux explicite cette variation séquentielle. La notion temporelle expliquant pourquoi et comment tel ou tel endroit a été connecté avec tel ou tel autre. « L'espace […] n'obéit pas au sacro-saint modèle du centre et de la périphérie, mais il s'organise selon le modèle du réseau ; c'est un « tissu de nexus », une chaîne aux mailles fluides. L'espace n'est pas un pôle avec des marges, c'est une route ; avec un début et plus loin un infini. Le paysage reproduit cette image et la société s'ordonne sur elle » (Desmarais, 1998, p. 400). L'espace est un système plus ou moins complexe ayant une morphologie. Dans le dictionnaire critique de Roger Brunet, l'espace géographique « est l'étendue terrestre utilisée et aménagée par les sociétés en vue de leur reproduction. […] Il comprend l'ensemble des lieux et de leurs relations. […] L'espace géographique est donc à deux faces. Il est un système de relations et un produit social organisé, l'un des nombreux produits de l'activité sociale. »
Le but principal de l'espace géographique est d'expliquer « pourquoi cet élément est là et pas ailleurs ? ». La position dans l'espace n'est donc pas neutre. L'espace est une cause à part entière. C'est par essence une question topologique. Pour la résoudre en partie, il faut étudier la position des points les uns par rapport aux autres. Le terme « point » ne convient pas à la géographie. Il faut lui préférer « lieu » ou « endroit » qui induisent une notion de surface, de volume, d'étalement, et des formes qui leur sont propres. Là, intervient la notion d'échelle, quelle est l'échelle la mieux adaptée pour décrire un phénomène ? L'échelle dans laquelle le géographe doit se placer dépend de ce qu'il veut montrer. Il doit par conséquent avoir un sujet ou une problématique, qui doivent s'articuler à des échelles différentes. Telle ou telle échelle expliquant mieux les problèmes posés. L'échelle représente également le niveau d'existence d'une forme. Elle consiste à faire émerger des bornes, des limites, en rendant visible ou invisible telle ou telle forme terrestre.
4.2.3.1. L'approche classique de l'espace géographique
Classiquement, l'analyse spatiale sépare l'espace absolu (géographie physique), l'espace relatif (géographie physique et géographie sociale) et l'espace vécu et perçu (géographie sociale).
4.2.3.1.1. L'espace absolu
L'espace géographique d'Emmanuel Kant est défini comme absolu c'est-à-dire un support. Dans cette perspective, l'espace est indépendant de la matière. « L'espace absolu est un cadre dans lequel s'inscrivent des objets et les événements » (Bailly, Béguin, 1982, p. 59). Cet espace permet de quadriller la terre en suivant un système de coordonnées globalement sphériques (courbe), mais localement rectangulaire (non courbe). C'est une conception géométrique de l'espace. Cela a pour conséquence de transformer une position en un point, ce qui rend possible la jonction entre ces points, soit par un arc, soit par un segment, et ainsi définir une distance. Il est également possible d'obtenir un ensemble fermé à partir d'au moins trois points grâce à la théorie des surfaces et du plan (base de la cartographie). Enfin, il est possible de créer un volume à partir d'au moins un point à l'extérieur d'un plan dans lequel se trouve une surface (modèles numériques de terrain, images véristes, etc.).
Dans ce cadre, « le lieu est alors considéré comme un point de la surface terrestre défini par sa latitude et par sa longitude » (Bailly, Béguin, 1982, p. 59), ainsi que son altitude. On pourrait ajouter le temps car, dans de nombreux cas en géographie, la position reste fixe mais le temps continue de s'écouler au sein de cette position. Cette définition du lieu est bien sûr très restrictive. Nous y reviendrons.
Dans la définition kantienne, « l'espace est alors une catégorie sans substance : il est un contenant et la substance est un contenu. En géographie, cela équivaut à distinguer la localisation (définie par un langage spatial comme celui des coordonnées) des propriétés du contenu (définies par un langage de substance) » (Bailly, Béguin, 1982, p. 59). Cet espace permet donc de répondre à une des problématiques de la géographie, commune d'ailleurs avec la cartographie : « où se localise tel ou tel élément ? ». L'espace absolu est donc celui des structures et des organisations spatiales.
4.2.3.1.2. L'espace relatif
L'espace relatif est l'espace dans lequel s'applique le principe d'interaction spatiale. « Dans cette optique, l'espace (et son élément le lieu) n'est plus seulement définissable par des coordonnées mais également par des propriétés attachées à des substances (au sens philosophique). L'espace devient à la fois le contenant et le contenu : c'est l'espace dit « relatif ». » (Bailly et Béguin, 1982, p. 59). L'idée n'est pas neuve en soi : on la retrouve également chez Emmanuel Kant. « Le monde est le substrat et la scène où se déroule le jeu de notre habileté » (Kant, éd. 1999, p. 67). Autrement dit, un lieu est « davantage qu'une simple localisation, davantage qu'une latitude et une longitude » (Bunge, in Bailly, Béguin, 1982, p. 59) et qu'une altitude. C'est donc l'espace acteur.
4.2.3.1.3. L'espace perçu et l'espace vécu
Dans les espaces perçu et vécu, on étudie plus le système des acteurs agissant sur cet espace. « Le sens des lieux dépend des pratiques sociales et des vécus psychologiques comme le montre Armand Frémont (1976) » (Bailly, Béguin, 1982, p. 61). Armand Frémont a défini trois types de régions : la région fluide, la région enracinée et la région éclatée (fig. 10).
Région | Vécu |
|---|---|
Fluide | Sans attachement des hommes |
Enracinée | Liens profonds avec son environnement |
Eclatée | Espaces fonctionnels |
« Un lieu, quel qu'il soit, n'est rien pris en lui-même ; il est porteur de sens par ses relations avec d'autres lieux, d'autres hommes. Les axes de lecture de monde régional sont sélectionnés à travers nos représentations qui renvoient aux pratiques sociales et spatiales. L'image d'une région d'un lieu, correspond à un espace perçu ; dès lors, l'étude des représentations est fondamentale pour la compréhension des comportements spatiaux » (Bailly, Béguin, 1982, p. 61). Cela a été étudié à travers les cartes mentales par exemple.
Toutefois, dans ces approches, l'espace n'est pas pris en compte. En effet, ce n'est qu'un support neutre, passif, dépourvu de tout rôle dans le fonctionnement du système. D'ailleurs, jamais dans un système les variables spatiales sont prises en compte. L'espace géographique est donc un potentiel que les acteurs et les agents réexaminent et réévaluent continuellement en fonction de leurs besoins et de leurs aspirations, généralement au regard des dynamiques et des potentialités des autres territoires. Cette dynamique incessante conduit à d'éventuels repositionnements des lieux et des objets dans le système. Ainsi, sont nés les systèmes dits spatiaux.
Généralement, on considère qu'un système spatial est un système présentant une dimension spatiale. Ce système permet l'étude la connexion entre les lieux. Autrement dit, l'espace est une partie prenante de la dynamique de système. L'espace est alors découpé en unités spatiales dont le nombre et la forme varient selon le type de spatialisation retenu comme la grille à maille carrée. En réalité, il s'agit plutôt d'un système localisé dans l'espace géographique car le propre d'un système est d'être a-spatial. On note alors un problème conceptuel important. Un « système spatial » présente une certaine forme de non sens. En effet, un système est a-spatial : il concerne l'énergie (constante par rapport aux temps), l'information et la matière. Dans ce cadre, l'espace géographique est un support, et non un agent, ce qui présente une aporie par rapport au projet de l'analyse spatiale. En effet, quand il y a projection d'un espace quelconque, il y a projection d'un système d'intentions (contrôles). L'espace est donc construit par l'acteur. L'espace devient territoire d'un acteur dès qu'il est pris dans le rapport social de communication. Il n'existe qu'en fonction des visées intentionnelles de l'acteur.
A contrario, l'espace géographique est par définition « a-systémique ». Il ne peut pas y avoir de temps. En effet, d'après Roger Brunet (1980), « une organisation spatiale peut se définir comme un ensemble plus ou moins cohérent de lieux mis en relation. Cet ensemble est à la fois différencié et intégré en aires et réseaux dans lesquels circulent les flux ». Les systèmes spatiaux se caractérisent par deux éléments : (1) la dualité entre l'homogénéité et l'hétérogénéité ; (2) l'interaction spatiale des lieux. Un nouvel intérêt pour la localisation et les variations dans l'espace se dessine dans bon nombre de discipline des sciences sociales. Quels sont les liens entre les particularismes locaux et la connexion entre les lieux ? Telle est la question fondamentale de cette approche.
4.2.3.2. L'approche axiomatique de l'espace géographique
Georges Nicolas-Obadia propose trois axiomes pour la géographie (1980, p. 56-57). (1) L'axiome chorologique s'énonce ainsi « peut être géographique tout objet (matériel ou immatériel) qui différencie l'espace terrestre ». (2) L'axiome de situation est le suivant : « peut être géographique, tout objet (matériel ou immatériel) en rapport spatial avec un objet situé (totalement ou partiellement) en un autre endroit de a surface terrestre ». Enfin, (3) l'axiome chronologique précise que « peut être géographique tout objet (matériel ou immatériel) dont les rapports non exclusivement spatiaux s'accorde avec des successions observées ». Toutefois, celle d'Antoine Bailly et de Hubert Béguin reste la plus célèbre.
Pour Claude Raffestin (1980, p. 136-145), « est géographique toute relation qui différencie l'espace terrestre » (p. 138).
D'après Antoine Bailly et Hubert Béguin (1979 ; 1982, p. 58-75), l'espace géographique reposerait sur quatre axiomes.
(1) Il existe un ensemble de lieux noté S.
(2) Il existe une longueur métrique dL définie sur S.
(3) Il existe une mesure de superficie μA définie sur (S, BA).
(4) Il existe une mesure de masse μi défini sur (S, BA) pour tout ![]() .
.
Par leurs quatre axiomes, les auteurs on t pour objectif de « représenter des réalités géographiques par des concepts mathématiques » (Bailly, Béguin, 1982, p. 67).
Bien que la bonne volonté des auteurs n'est pas à mettre en doute, leur axiomatisation n'en est pas une. Tout simplement parce qu'il n'y a aucune règle mathématique dans leur définition de l'espace géographique. À la rigueur, il s'agit de principes premiers. En effet, le premier axiome n'est pas satisfaisant pour deux raisons. La première est qu'il ne définit pas ce qu'est un lieu. La seconde est qu'il ne définit pas ce qu'est un ensemble. L'axiomatisation reste une procédure extrêmement rigoureuse. Elle ne peut pas se permettre de laisser des concepts sans définition. Le second axiome renvoie au principe d'interaction spatiale. Les auteurs définissent cet axiome par une longueur L et une métrique (non négativité, symétrie, identité, inégalité triangulaire). Ce ne peut pas être un axiome car longueur et métrique reposent sur une théorie mathématique qui possède ses propres axiomes ! Il s'agit au plus d'un outil. De plus, la définition de la métrique est euclidienne, or il semblerait qu'une métrique fractale soit beaucoup plus d'adapter au discours géographique. Le troisième axiome essaye définir l'étendue spatiale. Un sous-ensemble de lieux possèderait une certaine étendue spatiale. Pour cela, il faut une superficie notée [A] et une mesure de S, notée BA. On peut formuler la même objection que l'axiome n°2. En effet, la superficie renvoie à la théorie des surfaces qui, elle-même, possède ses propres axiomes. Le quatrième axiome se veut ajouter des attributs ou des caractéristiques des lieux (leur contenu). Il distingue deux attributs : l'attribut simple qui renvoie à un scalaire et l'attribut composé qui est une fonction d'attributs simples. Un attribut simple est noté ![]() . Il possède une dimension Di munie d'une unité convenant à i et une mesure non négative μiS définie sur (S, BA) et qui prend ses valeurs dans Di. Là, il y a une confusion profonde entre axiomes, théorie de la mesure et variable mesurée. Autrement dit, le quatrième axiome n'en est pas un.
. Il possède une dimension Di munie d'une unité convenant à i et une mesure non négative μiS définie sur (S, BA) et qui prend ses valeurs dans Di. Là, il y a une confusion profonde entre axiomes, théorie de la mesure et variable mesurée. Autrement dit, le quatrième axiome n'en est pas un.
L'axiomatique proposée est donc insuffisante et ne peut pas être considérée comme axiomatique. D'ailleurs, les auteurs le reconnaissent volontiers : « qu'il soit bien clair que la proposition de définition qui vient d'être présentée n'est pas la seule possible ni nécessairement la meilleure. La recherche reste largement ouverte, tant il est vrai que la théorie géographique tâtonne encore et éprouve parfois quelques difficultés à se détacher du verbalisme qui l'a longtemps habitée » (Bailly, Béguin, 1982, p. 69). Toutefois, l'axiomatique n'est pas intéressante pour définir l'espace géographique car l'axiomatique est une démarche où l'on pose un ensemble de règles mathématiques sans chercher à les comprendre, à la différence des principes premiers. Aussi, ce mémoire va présenter comment fonder la géographie sur des principes premiers. Préalablement, de nombreux principes ont été présentés, mais lesquels choisir pour définir la géographie.
4.2.3.3. L'approche par principes premiers
Il s'agit ici de proposer une définition mathématique de l'espace géographique. Claude Tricot, au cours du Géopoint 1980, avait dit « je pense qu'il est plus actuel de s'intéresser à la mathématisation de la géographie, à sa modélisation qu'à son axiomatisation » (1980, p. 26).
L'espace géographique est-il euclidien ? Oui, pour les cartographes. En effet, la carte est un espace euclidien qui permet de répondre à la question « où sont les objets ? ». L'espace du cartographe est avant tout mathématique. Il ne s'occupe que de position des objets dans l'espace. Malgré le problème mathématique de la courbure terrestre, l'espace reste localement plat, donc euclidien, ce qui rend la cartographie possible. Toutefois, à très petite échelle, la courbure se manifeste, et la géométrie qui devient pertinente est celle de Bernhard Riemann. Aujourd'hui, géométrie euclidienne et riemannienne ont été englobées par la géométrie fractale.
L'espace géographique est-il fractal ? En effet, dans la plupart de ces études, la géographie se fonde sur un espace non euclidien c'est-à-dire anisotrope. Elle est de trouver comment les objets se sont-ils retrouvés là ou sont-ils apparus ici ? Accessoirement, elle répond de temps à autre à la question : pourquoi là et pas ailleurs ? Elle essaye de comprendre les relations entre les objets qui se répartissent dans l'espace cartographique et/ou l'espace géographique (principe d'interaction). À partir de là, on peut fonder la géographie autour du principe de la relativité (d'échelle). L'espace géographique devient alors mathématique assimilable à un espace fractal au sens de Laurent Nottale.
On a souvent évoqué le lieu, mais qu'est-ce qu'un lieu .
4.2.3.4. Le problème du lieu et de sa délimitation
Aux origines du lieu, on trouve la chôra (Platon) et le topos (Aristote). Pour Platon, la chôra est le rapport entre l'être absolu et l'être relatif qui est une image imparfaite de l'être absolu. L'être absolu est éternel : il ne nécessite pas de lieu précis, tandis que l'être relatif est en devenir. Ce dernier a donc besoin d'un lieu qui est la chôra pour se développer. Il faut remarquer que le terme n'est pas défini par Platon, sauf par des comparaisons. À l'opposé, le topos d'Aristote renvoie à l'identité du lieu. Le lieu est immobile et il limite une chose. Autrement dit, la chose et le lieu sont dissociables : si chose bouge, le lieu se transforme en un autre lieu. Le lieu est un « espace dans lequel la distance n'est pas pertinente » (Lévy, Lussault, 2003, p. 555-565). Pour Paul Vidal de la Blache, la géographie est la « science des lieux », mais qu'est-ce qu'un lieu .
Pour Roger Brunet, le lieu est un point de l'étendue, un élément de base de l'espace géographique. Le lieu est identifié et identifiable c'est-à-dire délimité. Il s'agit d'un point singulier : le lieu A se différencie du lieu B. Cela renvoie au topos. C'est la « plus petite unité spatiale complexe de la société » (Lévy, Lussault, 2003, p. 555-565). Cependant, le lieu défini comme un point dans l'espace absolu est une définition proche du non sens pour la géographie. En effet, un lieu est au minimum une surface et au maximum un volume. De plus, le lieu défini comme un contenu dans l'espace relatif est également problématique pour la géographie car cela signifie qu'il faut pour faire de la géographie avoir des connaissances en économie, en démographie, en histoire, etc. Autrement dit, la géographie n'apporte qu'un support où des contingences locales se manifestent .
Qu'est-ce qu'un lieu en géographie ? Au final, on s'aperçoit que l'on fait appel à de nombreuses disciplines connexes pour définir un lieu. On peut désormais proposer une définition mathématique du lieu. Ce serait un objet fractal par définition, dans le sens où quelle que soit l'échelle (niveau de résolution), le lieu aura une certaine taille sur une carte. Une ville en serait l'archétype en géographie humaine. Le relief le serait en géographie physique.
4.2.3.5. Le lieu et le site
Quelle différence entre un lieu et un site ? Le site est un lieu qui possède un potentiel de localisation. Le site, au sens restreint, renvoie à l'idée de ressources naturelles, tandis qu'au sens large, il concerne également les ressources humaines.
La localisation renvoie à un état (où ?) et/ou une action (comment se situe-t-on ?). La situation possède deux définitions. D'abord, il peut s'agir d'un espace unique, d'un ensemble de configurations spatiales en interaction, permettant d'évaluer un site. Cependant, la situation peut être également définie par un jeu d'échelle. Autrement dit, toute situation renvoie à une localisation, et toute localisation définit une situation (fig. 11).
4.2.3.6. La répartition des lieux dans l'espace géographique
Expliquer la répartition des lieux dans l'espace géographique est au cœur de la géographie. Il existe trois manières d'aborder cette répartition sur l'interface terrestre. (1) La répartition est aléatoire, c'est-à-dire qu'elle obéit aux lois de la statistique. C'est une position de possibilisme : « il est possible que telle répartition obéisse à telle loi » ou « il est possible que la répartition actuelle évolue vers telle autre ». À l'opposé, (2) la répartition est déterministe, c'est-à-dire qu'elle possède des lois qui expliquent tout. Le principe de causalité est respecté en tout point de la démarche ; il n'y a en plus aucune incertitude.
Pendant longtemps, l'opposition de ces deux propositions a été très forte. La première correspond aux « cas pratiques », tandis que la seconde aux « cas théoriques ». Cependant, ce n'est pas pour autant que le hasard n'a pas de lois comme le croient beaucoup de scientifique. Il existe des lois du hasard régit par les probabilités, dont l'application sont les lois normales de la statistique.
Lorsque l'on les a appliquées en géographie, les résultats ont tellement été mitigés que beaucoup ont cru que cela ne fonctionnait pas. La position adoptée ici essaye de réhabilitait l'approche statistique des répartitions spatiales en géographie. En effet, l'explication du fait que ça ne marche pas est simple : les règles appliquées correspondent en fait à la mécanique newtonienne, c'est-à-dire la mécanique déterministe, linéaire et binaire. Aujourd'hui, il faut oublier cette mécanique newtonienne au profit de la mécanique quantique qui est probabiliste, non linéaire et ternaire dans de nombreux cas.
4.2.3.7. Conclusion partielle
Dans toutes les définitions, il est bizarre que l'on n'évoque jamais l'impulsion qui est comme on l'a vu, la grandeur fondamentale de l'espace, espace que l'on veut étudier ! De plus, à la différence du temps, une partie de l'espace géographique peut être objectivable via des outils comme la géométrie et/ou la topologie. La géographie a construit autour de ceux-ci son propre espace. La découverte de « l'espace-temps » par Albert Einstein permet de réconcilier deux concepts qui avaient été séparés par la « révolution copernico-galiléenne ». Ce mémoire essayant d'entrer dans le cadre de l'espace-temps, il faut définir et présenter brièvement. Aussi, il faut d'abord évoquer la place du temps en géographie et ensuite définir l'espace-temps.
4.2.4. La place du temps
Le temps n'a généralement aucune entrée dans un dictionnaire de géographie contemporain. Ainsi, pour parler du temps en géographie, il faut revenir à Fernand Braudel. Il avait défini le temps géographique de la manière suivante : il s'agit de la longue durée et la structure des deux autres. L'idée était de prétendre que c'était la scène dans laquelle les acteurs de l'histoire allaient venir jouer. « La longue durée est l'échelle de temps la plus pertinente parce que, mettant en évidence les régularités, elle est la plus « scientifique » » (Leduc, 1999, p. 27). Cette remarque est importante car l'histoire, dans sa « grande bonté », laissait aux géographes le discours scientifique et conservait le discours littéraire. Le temps et la géographie font donc de ces vieilles histoires sans fin, qui vivent ensemble par épisode.
Le temps géographique de Fernand Braudel est bien sûr le temps géomorphologique qui plante le décor. Il existe trois grands temps géomorphologiques. D'abord, la géomorphologie structurale représente la durée la plus longue et l'évolution y est micrométrique. Le déterminant est le mécanisme géologique qui permet, grâce aux cartes géologiques, de dater les structures géomorphologiques. Puis, la géomorphologie dynamique va passer à une durée et une évolution plus courte. Elle explique des mécanismes géologiques en court d'évolution. Enfin, la petite dernière, la géomorphologie climatique représente un intermédiaire entre la géomorphologie structurale et la géomorphologie dynamique. Il s'agit d'un temps moyen. Je ne sais pas si c'était volontaire, mais on retrouve dans le temps géographique de Fernand Braudel, trois autres temps, confortant la théorie des trois temps. Il s'agit d'un cadre moderne. La présence du temps en géographie est bien sûr liée à l'obstruction galiléenne des causes formelles. On a, par conséquent, surinvestit la question du temps. La durée et l'évolution étaient devenues une idée clé de la géographie. Les années 1960 vont tout bouleverser. L'espace revient en force. Deux étapes sont tout de même à noter : une première étape dans laquelle nous sommes toujours en grande partie, consistant à expliquer l'évolution de l'espace géographique et une seconde étape dans laquelle nous sommes en train de rentrer qui essaye d'expliquer l'espace géographique, non plus par une évolution même si l'idée reste, mais par les structures spatiales elles-mêmes. Le temps, dans cette perspective, devient secondaire, « un accident de l'espace ».
L'approche temporelle, paradoxalement ou heureusement, reste essentielle. Parmi ces grands défenseurs, on trouve Christian Grataloup (1996). Il invente deux notions, plus ou moins spatio-temporel, l'événement géographique et la période géographique. L'événement géographique est le « changement significatif d'une logique spatiale » (Grataloup, 1996, p. 198). Quant à la période géographique, elle est la « durée historique pendant laquelle un même système spatial se reproduit » (Grataloup, 1996, p. 199). Grâce à ces deux concepts, la géohistoire a pu être refondée sous un angle différent de Fernand Braudel. En effet, ce dernier ne voyait que la géographie physique, tandis que Christian Grataloup considère bien l'espace comme un « acteur » évoluant dans le temps.
Ainsi, en géographie, il faut privilégier l'espace, sans négliger le temps. Cependant, le temps demeure une cause. Comment faire de l'espace une cause, sans tomber dans le déterminisme ? La solution serait bien d'identifier l'espace géographique à un espace quasi-quantique. Avant cela, il faut définir ce qu'est un espace-temps.
4.2.5. L'espace-temps en géographie
Le concept d'espace-temps est déjà relativement ancien. Il aura bientôt un siècle, tout en demeurant relativement peu connu des sciences humaines. Celles-ci l'ont ignoré, ne comprenant pas que leur calage sur les sciences dites dures en est profondément modifié. Les sciences humaines se sont toutes « modernisées » très difficilement. Certaines ne le sont que depuis une cinquantaine d'années. Comment peuvent-elles admettre que la science moderne qu'elles ont adoptée soit déjà en train de muter, et qu'il leur sera nécessaire d'entrer dans la perspective d'une pensée « transmoderne » ? L'espace-temps est de l'ordre de l'utopie en sciences humaines. Seules la géographie et l'archéologie de terrain ont produit quelques réflexions fondées sur ce concept, dans la mesure où elles sont constamment confrontées à des causes formelle et finale. En géographie, l'étude des dynamiques a été modélisée mathématiquement grâce aux travaux d'André Dauphiné (1987 ; 1995 ; 2003), de Denise Pumain (1997 ; 2001) en particulier. En archéologie, l'étude a été faite par Gérard Chouquer (2000). Cependant, les autres sciences humaines n'y ont toujours que peu réfléchi, l'espace-temps étant perçu comme quelque chose de négligeable, face au seul temps qui explique tout, grâce à son « statut » de cause efficiente.
L'espace-temps en géographie est diverse et varié. André Dauphiné a défini le projet de la géographie comme étant l'étude des systèmes spatio-temporels. Toutefois, l'espace-temps désigne tout et n'importe quoi en géographie. Il faut le reconnaître. La réflexion d'Emmanuel Kant sur le temps et l'espace semble pertinente pour la géographie. Pour lui, l'espace est le fondement de toutes les intuitions. « Je ne puis ni me représenter quelque chose sans étendue spatiale, ni l'espace lui-même comme divisé ou n'existant pas » (Kant, in Kunzmann, Burkard, Wiedmann, 1993, p. 137). L'espace est donc, a priori, le fondement de notre perception phénoménologique. Cependant, il est aussi au cœur de notre explication scientifique : il fonde notre façon de mesurer. Autrement dit, l'espace peut être considéré comme une géométrie pure. Toutefois, pour Emmanuel Kant, le temps n'est pas plus objectif que l'espace. Il demeure profondément ancrer dans notre sensibilité. Il représente l'ordre c'est-à-dire une succession logique d'événements. Enfin, pour Emmanuel Kant, temps et espace possèdent tous deux une réalité empirique et une identité transcendante. Ils sont fondamentalement phénoménologiques. N'oublions pas que Emmanuel Kant avait professé un cours de géographie entre 1755 et 1796, soit quasiment toute sa vie. Il a été recomposé à partir des notes de ces étudiants. La géographie a été pour la première fois publiée en 1802. Le projet de la géographie y est clairement énoncé comme étant la description et l'explication des formes par les outils mathématiques et physiques. Aujourd'hui, les théories physiques les plus importantes sont sans aucun doute celles de l'espace-temps.
« Tout ce qui bouge, bouge parce qu'autre chose bouge » (Aquin, in WW, 1995). Cette citation est pertinente pour définir le caractère mobile de l'espace géographique et de ces différents acteurs et agents. La géographie est un système dynamique qui pourrait être comparé à un film. Qu'est-ce qu'un film ? C'est une succession d'images légèrement différentes dont la mise en relation par un appareil mécanique permet de percevoir un mouvement, au travers lequel un temps est à la fois perçu et mesuré. Autrement dit, la dynamique spatiale de la bande du film génère l'impression et l'expression d'un temps. L'espace géographique peut être assimilé à cette vision à une nuance près. Nous voyons à la fois un film achevé et nous sommes dans un film en train d'être tourné. Etudier l'espace géographique revient donc à la fois à le rembobiner, c'est-à-dire étudier sa temporalité, et à comprendre sa morphologie, c'est-à-dire étudier sa structure. L'espace géographique doit privilégier ce dernier aspect. La temporalité n'est qu'un accident du mouvement des formes spatiales de l'interface terrestre.
4.3. Espace géographique et échelles
En sciences humaines, l'espace pose, comme dans les sciences dites dures, un problème de définition. René Descartes rattache le concept d'espace à la notion d'étendue et d'immensité. Il introduit une notion d'échelle puisqu'il différencie l'échelle humaine, mesurable, définissable ; et les échelles non humaines immesurables, indéfinissables. Ainsi, dans sa définition, il émet l'hypothèse que l'on ne peut pas expliciter une partie du mot.
Dans la définition de l'espace de René Descartes, on perçoit grâce à l'ordre scalaire, que l'espace est un concept géographique. Dans la géographie vidalienne, l'espace a été souvent synonyme d'espace cartésien, faisant de la géographie une science du lieu. Cependant la géographie n'a d'intérêt que si elle prend en compte l'espace. Ainsi d'une science du lieu, on est passé, dans les années 1960, à une science de l'étendue. Ce fut le remède trouvé à une géographie vidalienne gisant complètement à l'agonie dans le panorama des sciences. Le mot « espace » a relancé la discipline. L'absence de définition du terme a scindé en deux la géographie humaine. De cette coupure, ont émergé la géographie culturelle et l'analyse spatiale. Une géographie physique résiduelle restant essentiellement la science du lieu vidalienne et une géo-chronologie. Pour exister, la géographie doit essayer de trouver une définition claire de son espace, afin de pouvoir redéfinir sa place au sein des autres sciences.
Comment la géographie a-t-elle articulé l'espace et les échelles ? Il faut d'abord distinguer l'échelle cartographique de l'échelle géographique. L'échelle cartographique constitue une discrétisation arbitraire : 1/50 000, 1/25 000, 1/100 000 pour l'I.G.N. C'est un rapport homothétique, alors que l'échelle géographique est « un rapport entre la réalité et son interprétation » (Robert Ferras).
L'échelle présente quatre problèmes essentiels en géographie :
(1) le problème de la perte d'information due au découpage et à la hiérarchisation dans l'espace ;
(2) le problème de la taille qui nécessite un besoin de changer d'échelle (démarche multiscalaire) ;
(3) [ou (1)+(2)] le problème de l'emboîtement qui nécessite l'appel au concept d'échelle critique et qui nous ramène au problème de la morphogenèse qui serait due au rapport continu entre les échelles constructives de l'objet et à l'existence de limites ou discontinuités naturalisables ;
(4) l'échelle comme ordre de grandeur. On a besoin d'une échelle pour mesurer le temps et l'espace.
L'échelle et les autres disciplines. Il existe deux échelles en économie : l'échelle micro et l'échelle macro, encore, l'échelle individuelle et l'échelle collective en sociologie. L'échelle sociale crée une hiérarchie.
Il existe deux niveaux dans l'utilisation des fractales en géographie :
(1) la description et l'explication des objets d'étude fractals ;
(2) l'application des statistiques parétiennes.
Pierre Frankhauser et Denise Pumain (2001) constatent qu'il est difficile de traiter les problèmes géographiques avec les fractales. Pourtant, il est évident qu'elles sont utiles. La relativité d'échelle a essayé de les rendre, enfin, utilisable.
L'échelle engendre la limite, ce qui règle la question de la taille. En effet, tant que l'on n'est pas à la bonne échelle, on ne peut pas perçoir la limite de l'objet géographique, donc de sa forme. « Le monde des géographes est avant tout un monde de formes… » résume André Dauphiné (2003, p. 148). En effet, le projet scientifique de la géographie est d'expliquer les formes déployées de et sur l'interface terrestre. Autrement dit, l'idée clé de la géographie est de prétendre que la position dans l'espace, au sens très général du terme, n'est pas neutre et qu'il a un sens, ce qui revient souvent à étudier le rapport entre le continu et le discontinu. Celui-ci est l'adage de toute science. La physique, par exemple, étudie les deux : une première approche est presque toujours discrète (discontinue) et une seconde est continue par l'établissement d'une fonction. En géographie, l'étude des formes nécessite une approche par la limite des objets géographiques. Quelle est la limite d'une montagne, d'un bassin versant, d'une ville, etc. ? Autrement dit, la géographie étudie, avant tout et de manière essentiellement phénoménologique, les discontinuités spatiales, à savoir comment tel objet se différencie de tel autre ? Les discontinuités en géographie sont généralement identifiées grâce à une méthode d'emboîtement d'échelle : l'approche multiscalaire.
En effet, la géographie a toujours souligné le problème des échelles que soient la géographie vidalienne ou la géographie spatiale ou la géographie humaniste. Comme les réflexions issues de la question d'agrégation « Echelles et temporalités » (2004-2005) l'ont montré, le terme « échelle » est polysémique. L'approche traditionnelle est mathématique. L'échelle est un outil technique permettant de représenter un objet sur le papier avec une taille réduite, grâce au concept mathématique d'homothétie. Autrement dit, l'idée est que l'objet réel se trouve représenter sur le papier par une longueur « abstraite ». Un objet géographique nécessite une telle représentation. Un géographe étudiant sur une montagne par exemple, aura beau se balader au cœur de celle-ci, s'il n'utilise pas une carte topographique, ou mieux un modèle numérique de terrain, il ne pourra jamais obtenir une information globale de cette montagne. Ainsi, la réduction de son objet d'étude a une échelle de 1/25 000 par exemple, est indispensable, mais il faudra sans doute qu'il utilise la carte au 1/50 000 et celle au 1/100 000. Le problème majeur de cette recherche d'emboîtement d'échelle est que les coupures de l'Institut géographique national (I.G.N.) demeurent arbitraires.
Pour résoudre cette difficulté, au début des années 1990, certains géographes se sont lancés dans l'approche des échelles par la géométrie fractale, inventée par Benoît Mandelbrot dans les années 1960. En 1975, Benoît Mandelbrot écrivit son premier ouvrage de vulgarisation Objets fractals. C'est dans ce livre que nous trouvons des applications géomorphologiques, dont l'exemple le plus célèbre est la côte de la Bretagne. Cependant, l'approche des objets géographiques par les fractales semble s'essouffler en ce début du XXIe siècle. Pourquoi ? Les raisons sont multiples.
La première est une confusion sur la définition même des fractales. Paradoxalement, c'est l'ouvrage de 1975 de Benoît Mandelbrot qui en est à l'origine. Un objet fractal n'est pas obligatoirement auto similaire ! Aucune fractale naturelle ne l'est totalement. Il existe toujours ce que l'on appelle des échelles de coupure. Autrement dit, il ne faut pas faire une obsession de la recherche d'une régression linéaire dans un graphique bilogarithmique d'une fonction puissance. De nombreuses fractales en géographie ne présentent pas cette caractéristique et ce, sur des objets que Benoît Mandelbrot avait qualifié de fractal en 1975, comme les résultats obtenus sur le mont Aigoual ou le Lodévois qui présentent une régression polynomiale dans un graphique bilogarithmique (Martin, 2004b). Nous reviendrons plus tard sur cette confusion.
La seconde raison est la prise de conscience par certains géographes, fractalistes de la première heure, de l'effort mathématique à mettre en œuvre. En effet, la difficulté à appliquer les méthodes de Benoît Mandelbrot à la géographie, peut être expliquée par le fait que nous ne pouvons rien expérimenter en géographie. Autrement dit, mathématiquement, et c'est le drame de la géographie, nous ne pouvons pas partir du simple et arriver au complexe. Dès que nous ouvrons une porte, la complexité nous attend toujours derrière. Ainsi, l'espace géographique possède déjà un niveau de complexité très élevé. Et, les solutions mathématiques sont très élaborées. Cependant, cette solution demeure excellente par sa richesse et son originalité. La géométrie fractale permet donc une approche mathématique de l'emboîtement d'échelle, et plus largement de ce que les géographes appellent l'effet d'échelle.
De ce fait, pourquoi la majorité des géographes sont-ils passés à côté des fractales ? Voilà une excellente question. Benoît Mandelbrot (1975) fournit une quantité extraordinaire d'exemples provenant d'objets géographiques qu'ils soient physique (montagnes, nuages…) ou humain (villes…). Le fait d'employer le terme « objet » pose tout le problème. Jamais nous n'avons étudié, en géographie ou dans les autres sciences, autre chose qu'un objet fractal. En effet, qu'apporte le fait de prouver qu'un objet soit fractal ? En réalité, pas grand chose, car dans cette approche, la fractalité demeure une conséquence, et non une cause. De plus, depuis les années 1960, la définition même de la géographie se concentre dans un terme presque magique « espace ». Autrement dit, le problème des fractales en géographie peut être reformulé de la manière suivante : comment passer d'un objet géographique fractal à un espace géographique fractal .
La question a été en partie résolue en 1993 par le physicien Laurent Nottale. En posant le principe de relativité d'échelle, il a été amené à définir un espace fractal. Pourquoi l'utilisation d'un espace fractal serait-il plus intéressant pour le géographe qu'un objet fractal ? Tout simplement parce que l'objet est toujours défini de l'extérieur, c'est une conséquence, tandis que l'espace, lui, est défini de l'intérieur, c'est une cause. Autrement dit, et de manière un peu caricatural, s'il existe un objet fractal « montagne » que l'on décrit de l'extérieur, il existe également un espace fractal « montagne » dans lequel nous sommes la montagne, c'est-à-dire que nous décrivons la morphologie de la montagne par la montagne. Il en va de même pour un objet comme la ville.
De ce fait, il nous faut préalablement définir plus précisément ce qu'est un objet fractal et ce qu'est un espace fractal. Pour ce, nous devons faire appel à des mathématiques de haut niveau. Afin de ne pas perdre le lecteur non matheux dans une constellation d'équations, nous accorderons une très grande attention à la rédaction de l'explication de l'intérêt de ces équations pour un problème géographique, et plus précisément géomorphologique. La géomorphologie est ici prise dans un sens très large. Elle inclut aussi bien les formes humaines que les formes naturelles. Cette remarque est importante car le souhait d'une géographie mathématique devra être parfaitement compatible avec les différentes approches menées jusqu'à présent. Elle devra se présenter comme un complément théorique qui nous est apparu indispensable.
Cependant, cette approche mathématique ne convenant pas à certains géographes, comme les géographes « humanistes », aussi une définition phénoménologique du terme « échelle » a été proposée. « Le paradoxe – et la difficulté – est que l'échelle dans son usage le plus courant est liée à la proportion qu'elle accompagne : pour le cartographe 2 est 4 sur la carte comme 200 est à 400 sur le territoire du moment que la carte est à 1/100. Paradoxe auquel il faut mettre un terme : avec l'échelle il ne s'agit pas d'une règle d'homothétie mais d'autre chose. Et – les architectes vous le diront – quand la taille change les dimensions du monument, « l'échelle » concerne les rapports entre ces dimensions et celles du corps humain » (Boudon, 1991, in Volvey, 2005, p. 22). Le paradoxe phénoménologique souligné par Boudon est une première approche possible des espaces fractals. Ils correspondent bien à cette idée qu'à chaque niveau, il existe des structures différentes. Autrement dit, une organisation hiérarchique mathématique plus profonde découle de l'admission d'un espace géographique fractal parfaitement conforme à l'approche phénoménologique, ce qui peut paraître complètement paradoxale.
4.3.1. Espace géographique et dépendance d'échelle.
Tout objet géographique possède une échelle. C'est le B.A. BA de notre discipline. Cependant, son choix relève toujours d'un arbitre : le géographe qui l'a choisi. Aussi, d'après Roger Brunet, les différences n'apparaissent qu'à certaines échelles. C'est le cœur de l'idée de dépendance d'échelle, c'est-à-dire qu'un objet géographique est coincé entre deux échelles de coupure entre lesquelles son existence ne fait aucun doute. Le but de définir l'espace géographique comme étant un espace fractal est que ces échelles de coupure de chaque objet géographique deviendraient objectivables.
L'espace géographique fractal serait un concept précis qui renvoie à la théorie de la relativité d'échelle, mais dont la souplesse permettrait de ne pas trop se montrer rigide par rapport au statut de sciences humaines de la géographie. De plus, le lieu serait défini comme un objet fractal (donc se déclinant à diverses échelles) matériel ou immatériel dans cet espace géographique fractal. Quant au territoire, il ne serait un lieu particulier. Aussi, dans cette perspective, l'espace géographique deviendrait autant un acteur qu'un support, ce qui n'est pas contradictoire avec sa définition d'espace physique et d'espace humanisé. Ainsi, l'effet d'échelle serait de plus en plus pris en compte et de mieux en mieux maîtriser car « la mesure d'une chose dépend de l'outil de mesure que l'on utilise. Le mathématicien Benoît Mandelbrot a eu l'intuition de transformer « outil » en « échelle » » (Baudelle, Regnauld, 2004, p. 101).
4.3.2. Vers une géographie structurale ?
Nous allons ici reprendre l'idée de Gaëtan Desmarais et de Gilles Richot (2000). Toutefois, si l'on partage la nécessité d'une approche structurale en géographie, on diverge d'eux lorsqu'ils l'appliquent. La géographie structurale se présente comme étant issu du structuralisme.
Le structuralisme se décompose en trois temps : (1) le structuralisme dynamique en biologie autour d'Etienne Geoffroy Saint-Hilaire, Goethe et Waddington ; (2) le structuralisme linguistique de Ferdinand de Saussure et le structuralisme en sciences humaines de Claude Lévi-Strauss ; (3) le structuralisme morphodynamique de René Thom et de Jean Petitot. Ce courant de pensées possède quelques concepts particuliers comme celui de « champ morphogénétique » inventé par Waddington. Cependant, la véritable conceptualisation est née du courant de René Thom qui a proposé une physique des formes c'est-à-dire mathématiser les structures en tant qu'objet théoriques. De plus, ce courant fit la synthèse du structuralisme dynamique et du structuralisme linguistique.
Qu'est-ce qu'une structure ? En géographie structurale, il s'agit de « formes abstraites d'organisation, qui ne sont pas réductibles à leurs diverses réalisations matérielles. La géographie structurale relève d'une attitude rationaliste qui distingue soigneusement les objets de connaissance théoriquement construits des phénomènes empiriques accessibles à l'observation. Elle considère ainsi qu'il ne faut pas confondre les structures – qui sont des objets théoriques dont la réalité est rigoureusement démontrée – avec leurs manifestations tangibles. Les structures sont des morphologies abstraites qui émergent dynamiquement du substrat où elles s'incarnent. Elles conditionnent la stabilité et l'intelligibilité de leurs réalisations concrètes » (Desmarais, Ritchot, 2000, p. 11). Ainsi, « toute structure peut être définie comme un système de discontinuités qualitatives qui catégorisent un espace en une organisation relationnelle et dynamique de valeurs positionnelles (Desmarais, Ritchot, 2000, p. 11).
« La géographie structurale – qui conçoit les structures comme des formes abstraites en développement, des macro-morphologies se déployant dans des espaces substrats et émergeant dynamiquement de processus auto-organisés – s'inscrit dans le prolongement de l'unité rationnelle du structuralisme morphodynamique.
« Le programme de recherche de la géographie structurale consiste à décrire et à expliquer l'apparition, l'organisation, la transformation et l'évolution des formes aussi bien naturelles que culturelles présentes à la surface de la terre. L'approche n'est donc pas verticale. Elle ne tend pas vers une spécialisation accrue d'un secteur bien précis de la géographie, ni vers la promotion d'une nouvelle sous discipline qui pourrait prendre en charge une classe particulière de phénomènes. L'approche est plutôt transversale et concerne l'ensemble de la discipline géographique » (Desmarais, Ritchot, 2000, p. 12-13).
« La géographie contemporaine s'appuie sur la séparation entre les sciences de la nature et les sciences humaines. Malgré ses indéniables avancées, elle reste une discipline éclatée. La division entre les deux versants – physique et humain – donne lieu à un fractionnement d'où résultent de nombreuses sous disciplines et des spécialités de plus en plus morcelées qui composent un vaste catalogue dont les parties semblent entretenir peu de relations les unes avec les autres » (Desmarais, Ritchot, 2000, p. 124). Cependant, cette séparation est-elle un bien pour la géographie ? La réponse est mitigée. En effet, cette séparation garantit une certaine richesse discours, mais aussi une pauvreté et une ambiguïté des concepts et des théories géographiques.
Cette partie a très rapidement présenté la géographie structurale qui reste profondément polémique. Toutefois, leur approche de la géographie contemporaine est parfaitement réaliste et leur projet très proche de celui d'une théorie de la forme en géographie.
4.4. La position de la géographie sur les grands débats épistémologiques des sciences humaines
La longue histoire des sciences et des sociétés fondant les trois grands paradigmes (pré moderne, moderne et transmoderne) soulève des problèmes spécifiques qui disparaissent et réapparaissent. Les principaux sont la lutte entre l'holisme et l'individualisme, la nomothétique et l'idiographique et la position vis-à-vis du quantitatif et du qualitatif.
4.4.1. Holisme et individualisme
L'holisme est une doctrine épistémologique selon laquelle, face à l'expérience, chaque énoncé scientifique est tributaire du domaine tout entier dans lequel il apparaît. C'est une approche globalisante, nécessairement transdisciplinaire. C'est un vieux débat méthodologique en géographie qui suscite un regain d'intérêt aujourd'hui. L'idéal est de trouver un équilibre entre les deux. Avec l'analyse spatiale, une sorte d'holisme était apparue, notamment autour des méthodes empruntées à la systémique. Aujourd'hui, on assiste au grand retour de l'individu.
4.4.2. Nomothétique et idiographique
On oppose deux positions : celle des rationaliste et celle des empiristes. La position des rationalistes est idiographique, c'est-à-dire la recherche de l'individuel, du fait particulier. La position des empiristes est nomothétique, c'est-à-dire la recherche de l'universelle. Elle développe un aspect général et récurrent des phénomènes, pouvant à défaut d'énoncer les lois, du moins généraliser et parfois prévoir. La géographie vidalienne fut idiographique, celle de l'analyse spatiale nomothétique, et aujourd'hui, l'école sociale retourne vers l'idiographie.
4.4.3. Quantitatif et qualitatif
C'est sans doute le débat le plus vigoureux aujourd'hui. On assiste à une mathématisation de plus en plus prononcer du monde dans lequel nous vivons. Est-ce si utile ? Quels sont les principaux changements de la mathématisation au XXIe siècle .
4.4.3.1. La position des sciences de l'homme
La plupart des sciences de l'homme sont contre la mathématisation de leur discipline car trois obstacles surgissent : l'inadaptation de l'outil mathématique aux sciences humaines ; l'hostilité de ceux qui, ne connaissant pas les mathématiques, répugnent à les utiliser ; l'excès de zèle de certains, qui, par souci de modernisme prônent les mathématiques, sans se préoccuper de l'importance des problèmes abordés, ni de la portée des résultats obtenus. C'est dans cette dernière catégorie que se situe l'analyse spatiale.
On confond trop souvent mathématiques et quantification. Les mathématiques sont avant tout un langage, un moyen de quantification, or il existe deux types de mathématiques : les mathématiques qualitatives qui sont non numériques et ordinaux (topologie) et les mathématiques quantitatives qui sont numériques ordinaux ou cardinaux (analyse).
La géographie a tenté sa chance par le biais de l'analyse spatiale. Cependant, elle n'est restée qu'au niveau de la description mathématique. Elle n'a donc pas achevé son approche nomothétique.
4.4.3.2. Les transformations de l'outil mathématique
Quantifier relève de deux réalités : (1) énumérer, compter des unités, dénombrer les objets à étudier ou à décrire, relever la fréquence d'apparition d'un phénomène, (2) mesurer grâce à la référence à un symbole arbitraire.
Lorsque l'on mesure, il existe trois types d'erreurs. L'erreur de fait est un mensonge. L'erreur relative est due à un changement de données. L'erreur dans le passage du qualitatif au quantitatif présente le gros problème d'être involontaire et invisible. Une mesure est fidèle lorsque l'on emploie fréquemment le même outil. La fidélité réside dans la concordance d'observations, faites avec les mêmes instruments par des observateurs différents, sur les mêmes sujets. La validité de l'exactitude de l'outil connaît deux points de vue. D'un point de vue logique, un instrument est valide s'il mesure avec exactitude ce qu'il a pour but de mesurer. D'un point de vue empirique, un instrument est valide, dans la mesure où il permet de prédire avec exactitude. La précision d'un instrument se définit habituellement par sa sensibilité aux variations qu'il doit enregistrer.
4.4.4. Bilan constructif
Ces trois grandes positions qui sont au cœur des trois paradigmes, font toujours débat. Cependant, les trois paradigmes ne doivent pas être considérés comme des concurrents mais des pensées complémentaires qui offrent trois lectures possibles du monde à travers la connaissance scientifique. Il faut donc les croiser et les confronter dans ce but de comprendre. Pour conclure, on peut citer Gaston Bachelard : « l'essence même de la réflexion, c'est de comprendre qu'on n'avait pas compris. Les pensées non baconiennes, non euclidiennes, non cartésiennes sont résumées dans ces dialectiques historiques que présentent la rectification d'une erreur, l'extension d'un système, le complément d'une pensée » (1934, p. 178). La théorie des fractales et celle de la relativité d'échelle cherchent justement à offrir une possibilité de réflexion à de nouveaux concepts et de nouvelles lectures du monde.
5. Géographie et fractales
Cette partie est très technique et théorique. Elle a pour objectif de mettre fin aux idées reçues sur les fractales, véhiculées par certains géographes ou d'autres disciplines, mais aussi d'expliciter une définition généralisée des fractales qui permet de concevoir une « ballade » dans les différentes échelles d'un objet ou espace géographique fractal. On montrera ainsi que les discontinuités peuvent émerger d'une structuration en échelles, d'une organisation multidimensionnelle et fractale du monde et de la nature. Ainsi, le rêve d'une théorie des discontinuités (ou de la forme) en géographie pourrait prochainement devenir une réalité, d'abord sous la forme d'un classement morphologique, ensuite sous une celle d'approche purement mathématique. Pour le moment, il s'agit simplement d'une présentation lente et progressive des fractales car la fractalité des objets est bien la clé de la complexité discutée précédemment.
5.1. Les fractales et la géographie
Il n'est pas simple d'expliciter la géométrie fractale ni de démontrer son utilité en géographie, d'une part parce que les quelques géographes qui s'y sont intéressé, ont longtemps été en marge de la discipline ; d'autre part parce que nombreux sont ceux qui explique que très partiellement le concept même de « fractale ». Aussi, c'est dans cet esprit que, pour y remédier, cette partie a été pensée.
Elle sera peut être un peu trop didactique pour certains. Cela étant, un nombre de productions géographiques montre que le sujet touche la communauté qui y trouve matière à développer son projet. Toutefois, là où les choses sont peut être critiquables, c'est qu'une partie seulement du corpus fractaliste est mise en œuvre par les géographes. Il faut donc essayer d'optimiser son utilisation. La géographie, de part son positionnement académique, et en raison du rôle qu'y joue la notion d'échelle, est bien « armée » pour valoriser ce nouvel outil que constituent les fractales. Cependant, les fractales ont surtout servi à décrire des structures spatiales en géographie, et non à la fonder solidement dans une théorie géographique, théorie qui n'empêcherait pas du tout les discours phénoménologiques développés jusqu'alors.
5.2. Fractale, fractales ? Vous avez dit fractale ! êtes-vous sûrs ?
5.2.1. Notions élémentaires
5.2.1.1. Les fonctions logarithmiques
5.2.1.1.1. Le logarithme népérien
5.2.1.1.1.1. Définition
Soit la fonction 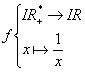 . La fonction f est dérivable sur
. La fonction f est dérivable sur ![]() . Elle admet donc des primitives. On appelle logarithme népérien la primitive qui s'annule pour x = 1.
. Elle admet donc des primitives. On appelle logarithme népérien la primitive qui s'annule pour x = 1.
![]()
5.2.1.1.1.2. Propriétés algébriques
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5.2.1.1.1.3. Etude de la fonction f(x) = ln x
![]() et
et ![]() .
.
![]() donc
donc ![]() .
.
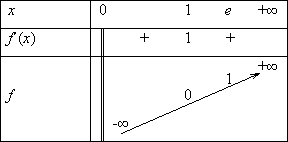
f est dérivable et strictement croissante sur ![]() .
.
f est une bijection de ![]() dans IR.
dans IR.
1 a un antécédent et un seul noté e. e est appelé nombre de Neper.
![]() avec
avec ![]() .
.
La tangente en e est ![]() .
.
5.2.1.1.1.4. Les fonctions composées de ln u.
Théorème. Si la fonction u est strictement positive et dérivable sur un intervalle I alors u est dérivable sur I.
![]() .
.
Fonction dérivée. ![]() avec
avec ![]() .
.
Fonction primitive. ![]() .
.
5.2.1.1.2. Les logarithmes de base a.
5.2.1.1.2.1. Définition.
On définit les fonctions logarithmes, notées loga x de base a telles que :
![]() .
.
Autrement dit, un logarithme de base a est proportionnel au logarithme népérien.
Le logarithme de base 10 est appelé logarithme décimal. Il est noté log x.
![]() .
.
Tous ces logarithmes ont les mêmes propriétés que le logarithme népérien.
5.2.1.1.2.2. Propriétés.
![]() et
et
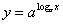 .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
5.2.1.1.2.3. Changement de base.
![]() .
.
5.2.1.2. Les fonctions exponentielles.
5.2.1.2.1. L'exponentielle de base e
5.2.1.2.1.1. Définition.
La fonction logarithme est une bijection de ![]() dans IR. La fonction réciproque de ln-1 est appelée fonction exponentielle de base e, note exp.
dans IR. La fonction réciproque de ln-1 est appelée fonction exponentielle de base e, note exp.
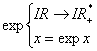 avec exp x > 0.
avec exp x > 0.
exp 0 = 1.
exp 1 = e.
5.2.1.2.1.2. Propriétés algébriques.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
Pour x = 1, on a ![]() .
.
Par convention, exp x sera notée ex.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
5.2.1.2.1.3. Etude de la fonction f(x) = ex
Soit la fonction f telle que ![]() .
.
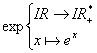 .
.
La fonction exponentielle est dérivable sur IR. Sa fonction dérivée est ![]() , tandis que sa fonction primitive est
, tandis que sa fonction primitive est ![]() .
.
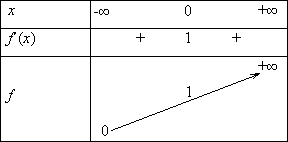
La tangente en 1 est parallèle à la tangente en 1 de la fonction logarithme népérien.
5.2.1.2.1.4. Les fonctions composées de eu.
Soit la fonction f telle que f(x) = eu(x). Le domaine de définition de f est le même que celui de u.
Si u est dérivable sur Df, eu est dérivable sur Df.
La fonction dérivée est eu est ![]() .
.
5.2.1.2.2. Les exponentielles de base a.
5.2.1.2.2.1. Définition.
Soit a > 0, on appelle fonction exponentielle de base a, notée expa, la fonction définie sur ![]() par
par ![]() . On note deux cas particuliers : si a = 1 alors expa x = 1. De plus, si a = e alors expe x = ex.
. On note deux cas particuliers : si a = 1 alors expa x = 1. De plus, si a = e alors expe x = ex.
Soit y = f(x) = ax où a est une constante quelconque et x une variable appelée l'exposant. f est une fonction bijective : x = loga y = f -1(x). En fait, la loi exponentielle de raison x fait correspondre le rang avec la série ordonnée a1, a2, a3, … Prenons un exemple :
| rang 1 | a1 |
| rang 2 | a2 |
| rang 3 | a3 |
| etc. | etc. |
Il existe deux propriétés fondamentales.
(1) expa(0) = 1. Autrement dit, chaque fonction exponentielle passe par ce même point.
(2) expa(1) = a. Autrement dit, l'image de 1 est le nombre de base de a.
5.2.1.2.2.2. Propriétés algébriques
![]() .
.
![]() .
.
![]() .
.
Pour x = 1, on a ![]() .
.
Par convention, expa x sera notée ax.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
5.2.1.2.2.3. Etude de la fonction f(x) = ax
Le domaine de définition de f est IR avec ![]() .
.
Sa fonction dérivée est ![]() .
.
Trois limites sont possibles.
(1) Pour a = 1, ![]() .
.
(2) Pour a > 1, il existe deux limites : ![]() et
et ![]() .
.
(3) Pour 0 < a < 1, il existe deux limites : ![]() et
et ![]() .
.
Pour les variations, deux cas sont possibles.
(1) Pour a > 1, expa est strictement croissante.
(2) Pour 0 < a < 1, expa est strictement décroissante.
5.2.1.3. Les fonctions puissances.
5.2.1.3.1. L'exposant rationnel.
5.2.1.3.1.1. Les puissances et les racines énièmes.
Soient ![]() et la fonction f telle que :
et la fonction f telle que :
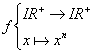 .
.
Sa fonction dérivée est ![]() .
. ![]() .
.
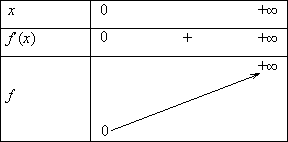
f est dérivable et strictement croissante sur IR.
f est une bijection de IR+ dans IR+. f admet donc une réciproque f-1 de IR+dans IR+, appelée racine énième.
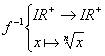 .
.
On note deux cas particuliers : si n = 1 alors ![]() . Si n = 2 alors
. Si n = 2 alors ![]() .
.
5.2.1.3.1.2. Les propriétés algébriques de la racine énième.
![]() .
.
![]() .
.
![]() .
.
5.2.1.3.1.3. L'exposant rationnel.
Soient ![]() . La racine q et la fonction exponentielle
. La racine q et la fonction exponentielle ![]() sont confondues sur
sont confondues sur ![]() .
.
La propriété caractéristique est la suivante : ![]() .
.
5.2.1.3.2. Les fonctions puissances.
Soit y = f(x) = xn. Par rapport à la fonction exponentielle de base a, exlna, adevient la variable et x la constante. Une loi puissance fait correspondre une ligne à la énième ligne. Prenons un exemple :
| ligne | 2n | 3n | 4n | 8n | … |
| énième ligne | 10n | 100n | 1 000n | 10 000n | … |
La variable x est le numéro de la colonne et n est un exposant fixe. Il faut remarquer que les exposants non entiers sont indépendants de l'ensemble des propriétés internes du système qu'ils décrivent.
Autrement dit, une fonction puissance est une fonction exponentielle de base a « freinée » par une fonction logarithmique de base a. Le cas le plus courant et le plus pratique demeure une base e. De toutemanière, tous les cas de base a se ramène à la base e. La démonstration est simple : ![]() . Il faut noter que l'ensemble de définition de la fonction x est
. Il faut noter que l'ensemble de définition de la fonction x est ![]() , ce qui signifie que la fonction x2, par exemple, ne sera définie que dans
, ce qui signifie que la fonction x2, par exemple, ne sera définie que dans ![]() , au lieu de IR en temps normal ! Il en va de même pour toutes les autres fonctions de ce type déjà connues. La fonction puissance x² n'est donc pas la même chose que la fonction élémentaire x², mais cela n'a rien de choquant puisqu'une fonction puissance est une fonction exponentielle c'est-à-dire une fonction toujours positive.
, au lieu de IR en temps normal ! Il en va de même pour toutes les autres fonctions de ce type déjà connues. La fonction puissance x² n'est donc pas la même chose que la fonction élémentaire x², mais cela n'a rien de choquant puisqu'une fonction puissance est une fonction exponentielle c'est-à-dire une fonction toujours positive.
5.2.1.3.2.1. Les fonctions puissances.
Soit la fonction ![]() avec
avec ![]() et constant. Le domaine de définition de f est
et constant. Le domaine de définition de f est ![]() .
.
La fonction dérivée des lois puissances est ![]() . Trois cas sont possibles.
. Trois cas sont possibles.
(1) ![]() .
.
(2) ![]() .
.
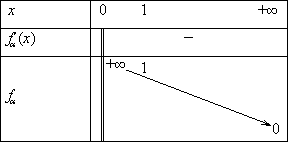
(3) ![]() .
.
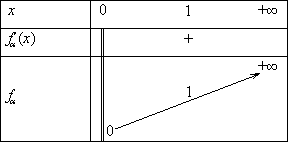
5.2.1.3.2.2. L'étude de la dérivabilité en 0.
Soit 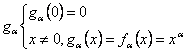 .
.
On calcule le nombre dérivé en 0 :
![]() .
.
À partir de là, deux cas se distinguent :
(1) Si ![]() , donc
, donc ![]() = 0.
= 0.
(2) Si ![]() , donc
, donc ![]() .
.
gα n'est pas dérivable en 0 mais il existe une tangente verticale par rapport à l'axe des ordonnées.
Enfin, pour ![]() .
.
5.2.1.4. Conclusion.
L'étude de ces trois fonctions est au cœur de l'approche par les fractales. Il faut donc bien maîtriser leurs propriétés algébriques et fonctionnelles.
5.2.2. La définition des fractales
Grosso modo, il en existe deux : celle du mathématicien Benoît Mandelbrot et celle du physicien Laurent Nottale. Elles ne sont pas contradictoires, mais celle de Laurent Nottale est plus générale.
5.2.2.1. Les concepts de distance et de dimension
Avant de définir ce qu'est une fractale, il faut préalablement éclaircir les notions de distance, de dimension, de dilatation et de contraction.
5.2.2.1.1. La notion de distance
Comment définir une distance ? La distance est une mesure qui nécessite au minimum quatre points : deux points servant à définir un étalon (le plus fréquent dans le monde étant le mètre) et les deux points dont on veut mesurer la distance. L'analyse fractale va étudier les rapports fonctionnels entre la distance et la dimension.
5.2.2.1.2. La notion de dimension
Soit une ligne droite de longueur L. Pour la mesurer, avec un étalon l, il faut reporter ![]() .
.
Pour mesurer une surface d'un carré de côté L et de surface L2, il suffit de compter le nombre de carrés de surface s tel que s = l2. Le nombre de carrés est donc ![]() , c'est-à-dire
, c'est-à-dire ![]() . De même, pour mesurer un volume d'un cube de côté L et de volume L3, il suffit de compter le nombre de cubes de volume v = l3. Le nombre de cubes est donc
. De même, pour mesurer un volume d'un cube de côté L et de volume L3, il suffit de compter le nombre de cubes de volume v = l3. Le nombre de cubes est donc ![]() , c'est-à-dire
, c'est-à-dire ![]() .
.
Si on pose, par exemple, ![]() . Cette affirmation est équivalente à
. Cette affirmation est équivalente à ![]() . Le nombre 2 est la dimension D de notre surface qui est égale à
. Le nombre 2 est la dimension D de notre surface qui est égale à 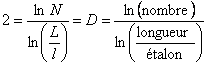 . On peut très facilement élargir cette définition de la dimension. En effet, on vient de calculer la dimension topologique (fig. 17) que présentent les formes euclidiennes. Il existe toutefois une dimension généralisée ou dimension fractale que l'on définira plus tard.
. On peut très facilement élargir cette définition de la dimension. En effet, on vient de calculer la dimension topologique (fig. 17) que présentent les formes euclidiennes. Il existe toutefois une dimension généralisée ou dimension fractale que l'on définira plus tard.
| dT = -1 | ensemble vide |
| dT = 0 | ensemble de points |
| dT = 1 | ensemble d'éléments d'une courbe, d'un cercle |
| dT = 2 | ensemble d'éléments d'une surface, d'un plan |
| dT = 3 | ensemble d'éléments d'un volume |
| dT > 3 | ensemble d'éléments d'un hypervolume |
Il faut préciser, enfin, que le terme dimension doit être réservé aux ensembles d'un strict point de vue mathématique afin d'éviter toute ambiguïté.
5.2.2.1.3. Les notions de dilatation et de contraction
Une homothétie est une transformation géométrique qui réduit ou agrandit une figure ou un objet mathématique. Lorsqu'il s'agit d'une réduction, on parlera de contraction. Lorsqu'il s'agit d'un agrandissement, on parlera de dilatation. À un premier niveau, une étude fractale consiste à essayer de comprendre comment s'articulent différentes homothéties dans un objet donné. Il s'agit donc d'une description d'un processus.
Mathématiquement, si l'on part d'une échelle λ1 et que l'on la dilate ou contracte d'un facteur ρ, on obtient une nouvelle échelle λ2 telle que :
λ1 = ρλ2.
Evidemment, si ρ > 1, on parle de dilatation et si ρ < 1, on parle de contraction. Si ρ = 1 alors il n'y a pas de transformation d'échelle (c'est une identité). Si ρ = 0 alors la transformation n'est pas possible.
Soit une nouvelle dilatation de λ2 par un facteur ρ' qui fournit une échelle λ3 telle que :
λ3 = ρ'λ2.
On admet que le rapport de dilatation entre λ1 et λ3est ρ'' = ρ'ρ, donc :
λ3 = ρ ρ'λ1.
Enfin, il est important de remarquer qu'une notation logarithmique permet de transformer les produits de dilatation en somme :
λ1 = ρλ2 ⇔ ln(λ1) = ln ρ + ln(λ2).
5.2.2.2. La définition de Benoît Mandelbrot
5.2.2.2.1. Les objets fractals
Une fractale (ou un fractal) est une figure ou un objet géométrique qui combine les caractéristiques suivantes (Mandelbrot, 1975, p. 154) :
(1) ses parties ont la même forme (ou structure) que le tout, à ceci près qu'elles sont à une échelle différente ;
(2) sa forme est, soit extrêmement irrégulière, soit extrêmement interrompue ou fragmentée, et le reste quelle que soit l'échelle d'examen ;
(3) il contient des « éléments distinctifs » dont les échelles sont très variées et couvrent une très large gamme.
« Les fractales sont des objets – qu'ils soient mathématiques, dus à la nature ou dus à l'homme – qu'on appelle irréguliers, rugueux, poreux ou fragmentés, et qui, de plus, possèdent ces propriétés au même degré à toutes les échelles. C'est-à-dire que ces objets ont la même forme, qu'ils soient vus de près ou de loin » (Mandelbrot, 1997, p. 33). Ainsi, il faut distinguer deux types d'objets : ceux relevant de la forme euclidienne de dimension topologique et ceux relevant de la forme fractale de dimension fractale.
« L'étude de ces objets constitue la géométrie fractale. […] C'est une géométrie du déterminisme chaotique » (Mandelbrot, 1997, p. 33). « Il ne s'agit pas vraiment d'une théorie, ni peut être même d'une discipline, mais plutôt d'une méthode. Son ambition de départ était celle de toute science : chercher des éléments d'ordre pouvant éclairer le chaos des messages que l'Homme reçoit de ses sens » (Mandelbrot, 1997, p. 33). « Je ne recommande pas la méthode fractale à tout le monde, ni n'ai jamais essayé de l'imposer à qui que ce soit », écrivait Benoît Mandelbrot (1997, p. 33). Ces affirmations sont en quelque sorte remise en cause par Laurent Nottale. Selon Benoît Mandelbrot, les outils de cette méthode sont au nombre de deux : (1) savoir voir ; (2) croire en la manifestation d'un « principe d'échelle » dont l'invariance d'échelle est la manifestation la plus couramment avancée. Cependant, l'usage montre qu'elle est très insuffisante. Laurent Nottale (1993) propose un cadre beaucoup plus général en parlant de dépendance d'échelle, dans laquelle l'invariance ne serait qu'un cas particulier et exceptionnel.
5.2.2.2.2. La dimension fractale
La dimension fractale est un « nombre qui quantifie le degré d'irrégularité et de fragmentation d'un ensemble géométrique ou d'un objet naturel, et qui se réduit, dans le cas des objets de la géométrie usuelle d'Euclide, à leurs dimensions [topologiques] » (Mandelbrot, 1975, p. 155). On parlera de poussières lorsque l'objet fractal possédera une dimension comprise entre 0 et 1. Une mise en garde doit toutefois être faite : la dimension fractale peut parfaitement être entière. C'est le cas, par exemple, du mouvement brownien où la dimension fractale est égale à deux dans un espace à trois ou quatre dimensions.
Pour définir une dimension, on a besoin d'une mesure, ou plus exactement d'une échelle de mesure. La mesure est définie par M(ε) = Nεd = Nμ où M est la mesure, ε est l'étalon, d la dimension, N le nombre de pavés obtenus par l'étalon, μ l'unité de mesure (longueur, volume, surface, masse…). Ce qui nous amène à une question fondamentale : quelle est la bonne mesure ? « La mesure est une préoccupation de base des mathématiques. Comment définir la mesure d'un ensemble ? Comment la mesurer ? Pourquoi ne peut-on pas mesurer une surface en mètres cubes, ou une longueur en litres ? Si […] la côte de la Bretagne n'a pas de longueur, c'est parce que la longueur n'est pas une bonne « mesure » pour un tel objet » (Sapoval, 1997, p. 64).
Qu'est-ce qui différencie un objet fractal d'un objet non fractal ? Et bien, simplement le fait que sa masse dépend du volume dans lequel on la considère : M(ε) = Nεd où M(ε) est la masse, N un préfacteur, ε le rayon d'un cercle ou d'une boule (ou encore d'un carré ou d'un pavé) et d la dimension du plan ou du volume ou de l'hypervolume. A contrario, la masse d'un objet homogène ordinaire, dans un espace à trois dimensions, est proportionnelle à son volume. La propriété fondamentale d'une fractale est que « la densité moyenne de matière d'une fractale autour d'un point décroisse quand on s'éloigne de ce point » (Sapoval, 1997, p. 172), ce qui est l'opposé de la loi gaussienne normale.
Il n'existe pas une, mais des dimensions fractales En 1975, Benoît Mandelbrolt vulgarisa la dimension de similitude et la dimension de Hausdoff-Besicovitch. Il faut maintenant présenter quelques unes de ces dimensions fractales.
5.2.2.2.2.1. La dimension de similitude
La dimension de similitude caractérise les objets auto-similaires. « Un objet est dit « auto-similiaire » si le « tout », c'est-à-dire l'objet tout entier peut être découpé en « parties », dont chacune se déduit du tout par une similitude, c'est-à-dire une réduction ou compression linéaire. Une telle réduction peut se décomposer en une homothétie suivie éventuellement par une translation, une réflexion et une rotation […]. On dit qu'un tel objet est « invariant par une famille de réduction » » (Mandelbrot, 1997, p. 40-41). « Du point de vue mathématique, le processus de réduction peut être rejeté indéfiniment. Il s'ensuit nécessairement qu'un objet mathématique auto-similaire contient des détails infinitésimaux » (Mandelbrot, 1997, p. 41).
« « Auto-similaire » peut signifier que toute partie de l'objet, convenablement « dilatée », peut être superposée sur une partie plus grande. Répétant ce processus indéfiniment, on voit qu'un tel objet, dit « invariant par dilatation », est nécessairement de taille infinie » (Mandelbrot, 1997, p. 41).
5.2.2.2.2.1.1. Quelques rappels mathématiques sur les similitudes
5.2.2.2.2.1.1.1. Définition
Une similitude est une transformation qui multiplie toutes les distances par un même nombre k non nul, appelé rapport de similitude. Par exemple, une homothétie de rapport ![]() est une similitude.
est une similitude.
5.2.2.2.2.1.1.2. Propriétés
Théorème 1. Les similitudes conservent les angles géométriques.
Théorème 2. Règle de composition entre deux similitudes.
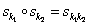 .
.Les similitudes conversent : l'alignement, le parallélisme, les barycentres et l'orthogonalité.
Les similitudes multiplient les distances par k, les surfaces par k2 et les volumes par k3.
5.2.2.2.2.1.1.3. Décomposition d'une similitude
Le catalogue des similitudes est le suivant : identité, réflexion, translation, homothétie, composée d'une rotation par une translation.
Il n'existe que deux types de similitudes possibles :
la composée d'une rotation par une homothétie qui est appelée similitude directe, c'est-à-dire qu'elle conserve les angles orientés. Les centres de la rotation et de l'homothétie sont supposés dans ce cas distincts ;
la composée d'une réflexion par une homothétie qui est appelée similitude indirecte, c'est-à-dire qu'elle ne conserve pas les angles orientés.
5.2.2.2.2.1.2. La dimension de similitude
La dimension de similitude est définie de la manière suivante :  où N est le générateur (généralement la longueur initiale) et
où N est le générateur (généralement la longueur initiale) et ![]() le rapport de partage. « Pour les ensembles auto-similaires, cette multiplicité [des dimensions] est en général sans grande importance : toutes les définitions finissent par donner la même valeur » (Mandelbrot, 1997, p. 53), mais pourquoi ? La théorie de la relativité d'échelle répond à cette question fondamentale, mais ne brûlons pas les étapes. En effet, la dimension de similitude ne convient pas aux fractales observées dans la nature car on s'aperçoit qu'elles « sont bornées et dépourvues de détails infinitésimaux » (Mandelbrot, 1997, p. 41).
le rapport de partage. « Pour les ensembles auto-similaires, cette multiplicité [des dimensions] est en général sans grande importance : toutes les définitions finissent par donner la même valeur » (Mandelbrot, 1997, p. 53), mais pourquoi ? La théorie de la relativité d'échelle répond à cette question fondamentale, mais ne brûlons pas les étapes. En effet, la dimension de similitude ne convient pas aux fractales observées dans la nature car on s'aperçoit qu'elles « sont bornées et dépourvues de détails infinitésimaux » (Mandelbrot, 1997, p. 41).
5.2.2.2.2.1.3 Les problèmes pratiques de la dimension de similitude
L'invariance d'échelle peut prendre d'autres noms : l'invariance par homothétie, l'invariance par dilatation ou la similitude interne.
En pratique, l'invariance d'échelle n'existe pas : elle est toujours bornée ou limitée par une gamme de distance r. Autrement dit, mathématiquement, on a a << r << A où a est la coupure à une distance microscopique due à l'étalon choisi et A est la coupure macroscopique due à la taille de l'échantillon, à la longueur de corrélation, à des effets de gradients…
En d'autres termes, l'invariance ne peut être vérifiée qu'asymptotiquement (avec r très grand) : c'est le concept de gamme d'échelle suffisante. S'il existe des corrections aux lois d'échelles, c'est-à-dire où le préfacteur varie en fonction de r. « En dessous de laquelle la géométrie est régulière, et une grande échelle, qui est simplement sa taille. Ces deux échelles se nomment coupure inférieure et coupure supérieure. La notion de fractale n'a évidemment d'intérêt que si ces deux échelles sont très différentes »b (Sapoval, 1997, p. 76). La relativité d'échelle explique ce passage entre coupure inférieure et coupure supérieure, c'est-à-dire entre la partie de la structure non fractale et la partie de la structure fractale.
Cependant, la dimension de similitude n'est qu'un cas particulier de la dimension de Hausdorff-Besicovitch.
5.2.2.2.2.2. La dimension de Hausdorff-Besicovitch
Dans la pratique, Benoît Mandelbrot a popularisé cette dimension. Il faut toutefois préciser qu'il ne s'agit que d'un exemple qui présente un cas plutôt théorique.
Soit un objet E, de forme quelconque. Il n'est généralement pas possible de le recouvrir avec des pavés identiques de côté ![]() , mais on peut faire le recouvrement de l'objet E avec des boules Vi dont le diamètre 2r est inférieur ou égal à ε :
, mais on peut faire le recouvrement de l'objet E avec des boules Vi dont le diamètre 2r est inférieur ou égal à ε :
![]()
C'est ce que l'on appelle la α-mesure de recouvrement. La dimension de Hausdorff-Besicovitch est définie comme :
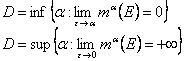
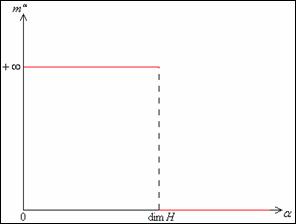
La dimension de Hausdorff-Besicovitch (dim H) est la valeur de α pour laquelle la mesure fait un saut de zéro à l'infini. Pour D = α, cette mesure peut être quelconque entre zéro et l'infini.
5.2.2.2.2.3. La détermination pratique de la dimension fractale dans un espace métrique
Il existe de nombreuses méthodes, en voici quelques-unes. Chacune aura pour dimension le nom de la méthode.
5.2.2.2.2.3.1 La méthode des boîtes
Une remarque préliminaire est à formuler en ce qui concerne cette méthode : la « dimension des boîtes » n'est pas la même chose que la dimension de Hausdorff-Besicovitch.
Soit N(ε) le nombre de pavés de côté ε recouvrant E :
![]()
La méthode des boîtes est couramment utilisée pour les structures auto-affines.
5.2.2.2.2.3.2 La méthode des boules disjointes
Soit N(ε) le nombre maximum de boules disjointes de rayon ε centrée sur l'ensemble E :
![]()
5.2.2.2.2.3.3. La méthode du compas
Soit N(ε) le nombre de « pas » de longueur ε nécessaire pour parcourir E :
![]() .
.
Toutes ces méthodes sont, en réalité, équivalentes dans un espace euclidien de dimension finie. D est la dimension de Bouligand-Minkowski.
5.2.2.2.2.4. Méthode de calcul de la dimension fractale d'un ensemble de points (Berge, Pomeau, Vidal, 1988, p. 159)
Un cercle (ou une sphère ou une hypersphère) de rayon r est tracé en prenant pour centre un point quelconque de l'ensemble.
On détermine alors le nombre N(r) de points situés à l'intérieur du cercle et sa variation en fonction de r.
Cas général :
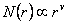 .
.Ensemble de Georg Cantor :
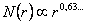 .
.Ligne (dimension 1) :
 .
.Surface (dimension 2) :
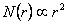 .
.
5.2.2.2.3. Les fractales auto-affine
L'auto-similarité fait appel aux transformations de la rotation et d'homothétie, c'est-à-dire une similitude, d'où son nom. Toutefois, elle ne serait couvrir la totalité du concept de fractalité. Benoît Mandelbrot (1997) a appelé auto-affinité, toutes les transformations linéaires plus générales de la forme :
S(x) = T.x + b (Dubois, 1995, p. 85)
où S(x) est une application de IRn dans IRn, T est une transformation linéaire sur IRn et x et b sont des vecteurs dans IRn.
« Une transformation affine S est donc une combinaison possible de translation, rotation, dilatation, contraction, ou même réflexion. À la différence des transformations par similarité, les transformations affines contractent ou dilatent avec des rapports différents dans différentes directions » (Dubois, 1995, p. 85).
Tout comme l'auto-similarité, l'auto-affinité se décomposent en deux types de processus : ceux qui sont déterministes comme l'escalier du diable et ceux qui sont aléatoires (coupe topographique de montagne, oscillations boursières).
Soit une variation Δf telle que Δf = f(t + Δt) – f(t). Une courbe auto-affine a une équation des différences de la forme :
![]()
où l'application S possède la forme :
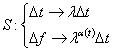
α(t) est appelé exposant de Hölder (1859-1937), un mathématicien, ou encore, exposant de Hurst (1880-1978), un hydrologue. Il présente la particularité d'être relativement stable. Il varie toujours entre 0 et 1. « Le comportement de α(t) fournit la base d'une distinction essentielle » (Mandelbrot, 1997, p. 54) :
(1) si α(t) est indépendant de t, l'objet sera dit unifractal ;
(2) si α(t) est dépendant de t, l'objet sera dit multifractal.
« L'auto-affinité implique plusieurs dimensions fractales et la multifractalité en implique une infinité » (Mandelbrot, 1997, p. 55-56).
Enfin, un théorème fondamental doit être signalé : « la coupe par un plan d'une fractale auto-affine est une fractale auto-similaire » (Sapoval, 1997, p. 213). Autrement dit, les courbes de niveau en deux dimensions d'un relief quelconque, par exemple, sont auto-similaires alors que le relief en trois dimensions est auto-affine.
L'auto-affinité telle que l'ont vue Benoît Mandelbrot et ses élèves, demeure un concept relativement ambigu. Cerner les cas d'auto-affinité présente de nombreuses difficultés pratiques car, finalement, elle est assez facilement confondue avec le concept de multifractalité qui renvoie lui aussi à une variation de la dimension fractale. La théorie de la relativité d'échelle permet de réduire cette ambiguïté comme nous le verrons plus tard. Pour l'heure, il faut nous atteler à définir la multifractalité selon Benoît Mandelbrot.
5.2.2.2.4. La multifractalité
Contrairement, à ce que l'on lit trop souvent, il s'agit bien d'une invention de Benoît Mandelbrot, dès les années 1950. Toutefois, il est vrai que le terme a été inventé par Frisch et Parisi dans les années 1980 lorsqu'ils étudiant la turbulence par cette méthode. Le caractère multifractal est attaché à l'hétérogénéité de la distribution, c'est-à-dire qu'il n'existe pas d'exposant unique la caractérisant. Autrement dit, l'exposant devient variable, c'est-à-dire que le processus de changement d'échelle se transforme en même temps que le changement d'échelle lui-même. On est donc obligé de créer une « fonction dimension fractale », appelée exposant de singularité. Effectuer une analyse multifractale revient à chercher ce que l'on appelle le spectre f(α) des singularités qui « peut être introduit comme une quantité qui donne une caractérisation relativement précise du degré de régularité et d'homogénéité d'une mesure fractale » (OMT, 1995, p. 6). Il faut également rechercher le spectre τ(q) qui va décrire un comportement de quantités « globales ».
Il s'agit ici de présenter succinctement la multifractalité à partir du manuel de Jean-François Gouyet (1992) et de : Ondelettes, multifractales et turbulence (1995).
5.2.2.2.4.1. Définitions
Soit μ une mesure quelconque et Supp μ son support.
5.2.2.2.4.1.1. L'exposant de singularité
On appelle exposant de singularité au point ![]() , la limite :
, la limite :
![]()
où ![]() désigne une boule centrée x0 et de taille ε. Il s'agit d'un exposant de Hölder particulier.
désigne une boule centrée x0 et de taille ε. Il s'agit d'un exposant de Hölder particulier.
Cet exposant mesure la singularité de la mesure au voisinage d'un point x.
5.2.2.2.4.1.2. Le spectre f(α) des singularités
Le spectre f(α) des singularités associé à la mesure μ est la fonction qui, à tout α, associe la dimension fractale de l'ensemble des points x0 tels que α(x0) = α :
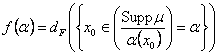
L'exposant de singularité en un point rend compte du degré local de régularité de la mesure considérée. La définition de α(x0) indique simplement que de manière générale, on pourra écrire :
![]() avec α ≥ 0 a priori quelconque.
avec α ≥ 0 a priori quelconque.
Plus la valeur de α(x0) est petite, moins la mesure est régulière autour de x0.
Le spectre f(α)des singularités décrit donc la répartition statistique des exposants α sur le support de mesure. Ainsi, si l'on pave le support de la mesure de « boîte » de taille ε, alors le nombre de ces boîtes dont la mesure varie comme εα pour un α donné, se comporte de la façon suivante :
![]()
Une mesure sera qualifiée d'homogène si son spectre des singularités est concentré en un seul point. C'est le cas des fractales auto-similaires ou auto-affines. Si le support de f(α) est large, la mesure considérée n'est pas homogène, l'exposant α(x0) fluctue d'un point à l'autre du support de μ ; on parle dans ce cas de mesure multifractale.
Le maximum de f(α) correspond à ![]() . Il a par conséquent une signification particulière. Enfin, à tout
. Il a par conséquent une signification particulière. Enfin, à tout ![]() ,
, ![]() avec
avec ![]() , le maximum de f(α) correspond à la mesure uniforme sur le support.
, le maximum de f(α) correspond à la mesure uniforme sur le support.
Enfin, il faut remarquer, pour mémoire, que le lien entre f(α) et αq sont les transformées de Legendre l'une de l'autre :
![]() ;
;
![]() .
.
5.2.2.2.4.1.3. Le spectre τ(q)
Soit une mesure τ(q) et un recouvrement de son support par des boules Bi(ε) de rayon ε. Soit N(ε) le nombre de boules nécessaires. On considère, pour tout ![]() , la fonction de partition
, la fonction de partition
![]() où on pose
où on pose ![]() .
.
On définit le spectre τ(q) à partir du comportement en loi puissance de Z(q, ε) quand ε → 0+
![]() ,
,
et le spectre des dimensions fractales généralisées comme le rapport :
![]() .
.
La dénomination « dimension fractale généralisée » se comprend si l'on remarque, d'après la définition ci-dessus, que pour q = 0, la fonction Dq est égale à la dimension fractale du support de la mesure Dq = dF. Pour q = 1, D1 caractérise le comportement dans les échelles de l'information (ou l'entropie) ![]() . Il faudra revenir sur son étude plus tard. On l'appelle dimension d'information. Pour q entier, q ≥ 2, Dq peut être relié au comportement des intégrales de corrélation à q points.
. Il faudra revenir sur son étude plus tard. On l'appelle dimension d'information. Pour q entier, q ≥ 2, Dq peut être relié au comportement des intégrales de corrélation à q points.
Les exposants τ(q) décrivent le comportement de quantités « globales », Z(q, ε), qui peuvent être considérés comme valeurs moyennes sur le support de mesure
![]() .
.
5.2.2.2.4.1.3.1. La signification de τ(q)
On considère la mesure suivante : ![]() . Que représente-t-elle ? On distingue quatre cas :
. Que représente-t-elle ? On distingue quatre cas :
quand q = 0,
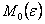 représente le volume du support mesuré en intervalle ε :
représente le volume du support mesuré en intervalle ε :quand q = 1,
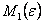 représente la somme sur le support des mesures dans l'intervalle ε :
représente la somme sur le support des mesures dans l'intervalle ε :quand q → +∞, Mq est dominée par les régions de très forte densité
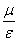 ;
;quand q → –∞, Mq est dominée par les régions de faible densité
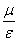 .
.
![]() avec D0 = 1 pour le segment [0, 1] ;
avec D0 = 1 pour le segment [0, 1] ;
![]() ;
;
Le paramètre q permet de sélectionner les sous-ensembles Eq correspondant à des densités plus ou moins grandes.
On pose ![]() . Les Dq sont appelées : dimensions généralisées d'ordre q. L'avantage de Dq sur les τ(q) réside dans le fait que ceux-ci se réduisent tous à la dimension fractale D quand l'espace est homogène c'est-à-dire :
. Les Dq sont appelées : dimensions généralisées d'ordre q. L'avantage de Dq sur les τ(q) réside dans le fait que ceux-ci se réduisent tous à la dimension fractale D quand l'espace est homogène c'est-à-dire :
![]() car
car ![]()
![]() .
.
Dq décroît de manière monotone quand q croît.
![]() avec
avec ![]() .
.
5.2.2.2.4.1.3.2. La forme et la signification de D1
Quand q = 1, l'expression précédente est indéterminée.
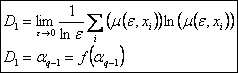
D1 est appelée dimension d'information. L'ensemble support Eα(1) contient presque toute la mesure de l'ensemble E.
L'exposant de masse de la distribution de mesure ![]() au moyen de la
au moyen de la ![]() mesure de recouvrement s'obtient comme la somme de volumes élémentaires
mesure de recouvrement s'obtient comme la somme de volumes élémentaires ![]() pondérés par leur mesure associée μq.
pondérés par leur mesure associée μq.
Soit ![]() , donc
, donc ![]() .
.
τ(q) est l'exposant de masse de la distribution μq.
5.2.2.2.4.1.4. Bilan
Jean-François Gouyet (1992) démontre que les liens entre f(α) et τ(q) sont les suivants :
![]()
et
![]()
avec cinq conditions :
(1) ![]() ;
;
(2) ![]() ;
;
(3) ;
;
(4) ![]() ;
;
(5)![]() .
.
Les grandeurs f(α) et τ(q) permettent de caractériser les hétérogénéités de distribution des mesures que l'on appelle mesures multifractales. L'analyse multifractale a pour but l'étude de fonctions dont la régularité ponctuelle peut varier d'un point. Le formalisme multifractal est basé sur la caractérisation suivante qui relie la régularité ponctuelle aux suprema locaux Dλ. Toutefois, ce résultat est valable si f est uniformément hölderienne, c'est-à-dire un cas très particulier de multifractalité.
En effet, on dit qu'une fonction f est uniformément hölderienne s'il existe ε > 0 et C > 0 tels que :
![]()
L'exposant de Hölder de toute fonction f uniformément hölderienne est donné par :
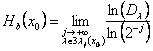
λj(x0) désigne l'intervalle dyadique de côté 2-j contenant x0 (donc 3λj(x0)) représente cet intervalle ainsi que les deux intervalles adjacents de même longueur.
5.2.2.2.4.2. L'approche statistique des multifractales
La variation de la dimension fractale, caractérisée par les spectres f(α) et τ(q), nécessite une approche statistique classique. On définit ainsi une mesure fractale suivant une loi binomiale et une autre suivant une loi multinomiale (Gouyet 1992 pour plus de détail).
5.2.2.2.4.3. Le problème inverse pour les fractales
Le problème inverse pour les fractales ne sera qu'évoquer dans ce mémoire simplement parce qu'il a été en partie résolu par l'approche de Laurent Nottale dans le cadre de la théorie de la relativité d'échelle. On appelle le problème inverse l'extraction « des données [d'] un système dynamique (ou ses caractéristiques principales) qui laisse invariant l'objet analysé, caractérisant par là son processus de construction » (OMT, 1995, p. 126).
5.2.2.2.4.4. Conclusion
L'approche statistique des multifractales est particulièrement « monstrueuse » et compliquée, et en plus, ne présente qu'un cas particulier de variation de la dimension fractale. Elle traduit bien une volonté de trouver un modèle discontinu. Ne serait-il pas plus simple de trouver un modèle continu encadrant cette discontinuité ? C'est ce que propose la théorie de la relativité d'échelle par l'intermédiaire du concept de djinn, où une partie de la multifractalité est expliquée comme étant solution d'une équation différentielle (donc continue) dans l'espace des échelles.
5.2.2.2.5. Les problèmes de la définition de Benoît Mandelbrot
Cettedéfinition des fractales (auto-similarité, auto-affinité, multifractalité) est incomplète et pose de nombreux problèmes épistémologiques et techniques.
Problème 1. De nombreux objets sont clairement fractales dans le sens où ils présentent une très forte irrégularité à toutes les échelles, mais ne sont pas invariants d'échelle que l'on soit dans le cas auto-similaire ou dans celui auto-affine. Il est donc évident que des objets invariants d'échelle sont rarement déployés sur l'interface terrestre.
Problème 2. L'ouvrage de vulgarisation de Benoît Mandelbrot (1975) a « trop bien marché ». Tout le monde s'est mis à calculer des modèles puissances, mais un peu n'importe comment. En effet, la plupart de ceux qui faisaient ces calculs ont oublié que, trouver une dimension fractale, nécessite une gamme d'échelle suffisante variant au minimum entre 100 et 106 .
Problème 3. Benoît Mandelbrot a défini les fractales à leurs limites. En géographie, par exemple, le choix de la limite d'un massif dont on calcule la dimension fractale est arbitraire. Autrement dit, ces calculs ne demeurent valables que dans le cadre du choix des données. De plus, se limiter aux objets, c'est nier l'existence même de l'espace géographique. Ne serait-ce donc pas plus utile pour la géographie d'adopter la définition des espaces fractals de Laurent Nottale .
Problème 4. Benoît Mandelbrot a lancé de nombreuses pistes sur les fractales, mais il n'a pas créé une véritable ligne directrice qui présente la théorie des fractales de manière cohérente. À savoir, pourquoi tel objet est « évidemment fractal » et tel autre est « évidemment non fractal », ou encore comment passe-t-on d'un objet non fractal à un objet qui l'est (et inversement).
Autrement dit, il faut mettre de l'ordre de ce pêle-mêle presque empirique qui a tendance à faire croire que l'on peut faire et écrire tout et son contraire à propos des fractales. C'est ce que propose la théorie de la relativité d'échelle de Laurent Nottale (1993). Au cours de la suite de cette partie, un cadre théorique précis va être défini pour caractériser les propriétés fractales d'un objet, et plus particulièrement d'un objet géographique. La partie suivante va présenter quelques applications pratiques de ce cadre théorique.
5.2.2.3. La définition de Laurent Nottale
Le physicien Laurent Nottale part de deux constats.
Constat 1. Toute expérience ou observation menée sur un système est réalisée à une résolution donnée.
Constat 2. Les états d'un système ne peuvent pas être définis de manière absolue, mais seulement de manière relative. Ceci s'applique à l'échelle du système : seuls les rapports d'échelles ont un sens, et non des échelles absolues.
Laurent Nottale n'est pas vraiment un « élève » de Benoît Mandelbrot. Il a plutôt découvert les fractales de manière indépendante en partant d'une hypothèse qui paraît évidente : toute mesure physique dépend de l'échelle à laquelle on la fait. Au cours de ses recherches, il a appris que ses objets dépendants d'échelle avaient été appelés « fractales » par Benoît Mandelbrot. Autrement dit, la définition de Laurent Nottale des fractales est légèrement différente de celle de Benoît Mandelbrot, comme il aime le préciser. De plus, bien évidemment, les deux définitions sont complémentaires, mais Laurent Nottale plante un décor beaucoup plus général et cohérent que Benoît Mandelbrot.
En effet, Benoît Mandelbrot a défini des « objets fractals » (1975), alors que Laurent Nottale parle d'« espaces fractals » (1993). Subtile nuance ? Non, tout simplement, parce qu'un objet est défini à sa limite c'est-à-dire de l'extérieur – si on veut faire une analogie avec la géographie, il s'agit d'un territoire, d'une région, d'un domaine, etc. – alors qu'un espace est obligatoirement défini de l'intérieur, ce qui signifie que l'on a donc plus besoin de limites pour caractériser le phénomène observé.
La suite des définitions présentera les résultats fondamentaux de la théorie de la relativité d'échelle de Laurent Nottale (1993). Il s'agit, pour une large partie, d'une traduction française du chapitre 3 de l'ouvrage de 1993, dûment complétée et remise à jour, mais surtout commentée. L'approche sera très mathématique dans le but de bien cadrer les différentes situations qui peuvent ou pourraient se présenter en géographie. Quelques applications en géographie seront présentées dans la partie suivante.
5.2.2.3.1. Les fondements des fractals
Le terme « fractal » a été attribué par Benoît Mandelbrot pour nommer des objets, des courbes, des fonctions, ou tout autre ensemble qui est extrêmement irrégulier et/ou fragmenté à toutes les échelles. Ces objets peuvent être caractérisés par des dimensions non intégrables et par leur non différentiabilité.
Deux ensembles ont la même dimension topologique si et seulement si on peut définir une transformation continue entre eux. Les dimensions topologiques demeurent intégrables. Cependant, des définitions alternatives des dimensions ont été données, comme celle de Hausdorff-Besicovitch, celle de la dimension de boîtes, celle de la dimension de recouvrement et la dimension de similarité. Les fractales sont habituellement définies comme des objets de dimension topologique DT, tels que D > DT.
Cette définition semble être trop restrictive, puisque beaucoup d'objets ou ensembles sont clairement fractals et peuvent avoir D = DT ou une dimension non constante ou une dimension bien définie. On va adapter à partir de maintenant, une définition différente. Les ensembles et les espaces que l'on appelle fractal sont caractérisés par leur échelle divergente. Cela signifie qu'ils sont des espaces métriques pour lesquels une mesure finie peut être définie, mais qu'une mesure standard (laquelle correspond à leur dimension topologique, c'est-à-dire la longueur d'une courbe, l'aire d'une surface, etc.) tend vers l'infini quand la résolution tend vers zéro. Cela inclut les fractales usuelles (une loi puissance divergente comme ![]() ) mais aussi les « sous-fractales » comme les divergences logarithmiques pour lesquelles D = DT, et les « sur-fractales » par exemple, les divergences exponentielles pour lesquelles la dimension formelle peut être infinie.
) mais aussi les « sous-fractales » comme les divergences logarithmiques pour lesquelles D = DT, et les « sur-fractales » par exemple, les divergences exponentielles pour lesquelles la dimension formelle peut être infinie.
| dT = -1 | ensemble vide |
| dT = 0 | ensemble de points |
| dT = 1 | ensemble d'éléments d'une courbe, d'un cercle |
| dT = 2 | ensemble d'éléments d'une surface, d'un plan |
| dT = 3 | ensemble d'éléments d'un volume |
| dT > 3 | ensemble d'éléments d'un hypervolume |
Un ensemble ou un objet a une dimension mesurée par des boules de rayon variable. La longueur d'un segment de « rayon » r est de 2r ; la surface d'un disque de rayon r est πr2 ; le volume d'une sphère est ![]() … Plus généralement, le contenu d'une boule de rayon r dans un espace de dimension d peut être défini comme :
… Plus généralement, le contenu d'une boule de rayon r dans un espace de dimension d peut être défini comme :
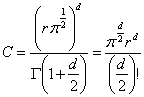
où Γ est une fonction gamma d'Euler.
le='font-family: Times New Roman;'>Cette relation est généralisable pour les dimensions d lesquelles ne sont plus intégrables. On considère un sous-ensemble compact F d'un espace métrique M. F peut être couvert par N(ε) boules de rayon inférieur ou égal à ε :

D n'est pas forcément entier.
La dimension de Hausdorff est une généralisation non nécessairement intégrable
![]() , où D > DT par définition.
, où D > DT par définition.
Ainsi, un chemin simplifié et très efficace pour décrire le recouvrement des fractals par des boules et rayons variables est identifié, par leur processus, avec la construction d'approximations successives de la fractale à résolution variable ε. On trouve que la d-mesure d'un sous-ensemble d'une fractale de dimension de Hausdorff D est obtenu par :
![]()
où la signification de la quantité finie ξ émergera graduellement à partir du suivant.
Les cas spéciaux considérés auparavant sont ainsi éclairés. Quand d = D, on trouve que la D-mesure d'un ensemble de dimension fractale D est la quantité finie, ξ dans l'équation ![]() . Quand d = DT cela implique l'existence d'une loi puissance divergente de la mesure usuelle (la dimension topologique). Cela est le cas le plus fréquent utilisé par l'interprétation physique et dans la mesure des dimensions fractales. C'est-à-dire que l'on tend naturellement à mesurer le nombre de points d'une poussière fractale, la longueur d'une courbe fractale, l'aire d'une surface, etc., lesquelles dépendent des résolutions comme :
. Quand d = DT cela implique l'existence d'une loi puissance divergente de la mesure usuelle (la dimension topologique). Cela est le cas le plus fréquent utilisé par l'interprétation physique et dans la mesure des dimensions fractales. C'est-à-dire que l'on tend naturellement à mesurer le nombre de points d'une poussière fractale, la longueur d'une courbe fractale, l'aire d'une surface, etc., lesquelles dépendent des résolutions comme :
![]() .
.
Quand ε tend vers zéro, ce DT-hypervolume est la production d'une quantité finie ξ laquelle est identifiée avec la D-mesure du sous-ensemble de la fractale considéré, et une quantité infinie, ![]() . Cette factorisation amène à un groupe de « renormalisation » des fractales.
. Cette factorisation amène à un groupe de « renormalisation » des fractales.
Une définition alternative pour la dimension fractale est la dimension de similarité. Les fractales auto-similaires de dimension de similarité D sont telles que quand on élargit par un facteur q, on obtient p = qD versions de la fractale initiale. La relation entre p, q et D est alors :
![]() .
.
Dans ce cas très simple, la dimension de Hausdorff et des dimensions de similarité sont identiques. On remarque que, dans ce cas, les fractales ont une propriété caractéristique : elles sont non différentiables.
5.2.2.3.2. La question de la différentiabilité de l'espace
5.2.2.3.2.1. L'espace-temps différentiable
Dans le cadre d'un espace différentiable, on a pour toute fonction les relations suivantes :
![]() où
où ![]() désigne la limite à droite et
désigne la limite à droite et ![]() , la limite à gauche.
, la limite à gauche.
![]() et
et ![]() .
.
5.2.2.3.2.2. L'espace-temps non différentiable
Dans ce cas, ces limites n'ont plus de sens, dt doit être considérée comme une résolution, et non comme un élément de différentiation. Il en résulte que, par exemple, la vitesse sur une trajectoire géodésique dépend explicitement de la résolution :
![]()
mais rien ne justifie que ![]() donc
donc
![]() .
.
Dans un espace non différentiable, ![]() .
.
L'abandon de la différentiabilité de l'espace-temps ne signifie pas qu'il faille abandonner la différentiabilité des grandeurs (physiques). La non différentiabilité de fonction L signifie simplement que :
![]()
au lieu de la traditionnelle limite
![]() .
.
Dans ce cas, dt → –dt éventuellement, on parle alors de brisure de symétrie, c'est-à-dire la brisure de l'invariance par « réflexion temporelle locale ».
Il existe aussi un autre type de brisure de l'invariance dite par « réflexion spatiale locale » dans le cas où dx → –dx.
5.2.2.3.2.3. L'opérateur différentiel de dilatation
Un opérateur est un outil mathématique qui relève en général du calcul différentiel qui décrit une action de transformation sur variation de la forme ![]() .
.
Une dilatation ou une contraction est une transformation de la résolution de la forme :
ε' = ρε
On définit une fonction L qui désigne une transformation d'échelle :
L(ε) = Kε–δ
Soit une dilatation ou une contraction infinitésimale ![]() à la résolution ε.
à la résolution ε.
On effectue ensuite un développement limité de Taylor pour obtenir :
![]() .
.
On pose Ď = ![]() , ce qui donne :
, ce qui donne :
L(ε' = (1+Ďdρ)L(ε)
où Ď est par définition l'opérateur de dilatation.
Leséquations différentielles d'échelle à construire vont donc impliquer des expressions telles que :
![]() .
.
Une telle équation et ses généralisations ne sont rien d'autre que l'équivalent différentiel de ce que sont les générateurs dans le cas des objets fractals construits par itérations, mais au lieu de passer d'une étape à la suivante de la construction à l'aide de dilatations finies discrètes, on passe de ln ε à ln ε + d ln ε. Ce sont des lois d'échelles. En d'autres termes, le calcul différentiel effectué dans l'espace des échelles permet de décrire un comportement non différentiable (à la limite) par des équations différentielles, ce qui apparaît incroyable. De plus, l'emploi des équations différentielles est possible grâce à une fonction de lissage définie comme telle et se retrouvant dans les équations.
5.2.2.3.3. L'espace fractal
Pourquoi passer à un espace ? Tout simplement parce que l'espace doit être défini de l'intérieur, à la différence d'un objet qui est défini de l'extérieur. De plus, la géographie spatiale a également pour objet d'étude l'espace géographique qui ne peut être qu'évidemment fractal, ne serait-ce que par ses fortes irrégularités.
5.2.2.3.3.1. Les courbes fractales dans le plan
La courbe de Van Koch se généralise dans le plan complexe en première approche par une base (ou un générateur). F1 est fabriquée de p segments de longueur ![]() . Les coordonnées des points Pj de Fj sont données par :
. Les coordonnées des points Pj de Fj sont données par :
img width=155 height=73 src="img/img-master-2-geo/image578.gif"> avec j = 1 à p.
On voit que le nombre de segments varie de 0 à (p – 1). Alors une autre représentation équivalente serait donnée par l'angle polaire du segment j, appelé ωj, ou l'angle relatif entre les segments (j – 1) et j, appelé αj. On choisit un système de coordonnées tel que F0 soit identifié avec le segment [0, 1]. La longueur des segments individuels est maintenant ![]() , et la dimension fractale sera donnée par :
, et la dimension fractale sera donnée par :
![]() .
.
La base F1 donne :
On constate que :
![]() et
et ![]() .
.
Pour j = 0, ![]() .
.
![]() avec
avec ![]() .
.
On note enfin que :
![]() et
et ![]() .
.
Cela est obtenu par la résolution de l'équation ![]() .
.
Un paramètre s peut être maintenant défini sur la fractale et peut s'écrire dans les termes de l'expression dans la base de comptage p :
![]()
avec sk prenant les valeurs intégrées de 0 à p – 1. Ce paramètre est une normalisation de la coordonnée curviligne sur une courbe fractale. La hiérarchie des figures reproduit la structure hiérarchique de la fractale, ce qui permet d'écrire l'équation fractale sous la forme :
![]() .
.
On a désormais :
![]()
et l'équation paramétrique de la fractale devient :
![]() .
.
Cette équation peut également être généralisée dans le cas où plusieurs transformations d'addition sont appliquées au générateur, ce qui peut être décrit par un opérateur, alors on obtient une généralisation :
![]()
![]()
où x(s) et y(s) sont les fonctions fractales dont les approximations successives sont xn(s) et yn(s).
La structure de l'équation ![]() est remarquable puisqu'il est évident que la partie jouée par p sur la fractale et q dans le plan :
est remarquable puisqu'il est évident que la partie jouée par p sur la fractale et q dans le plan : ![]() . Une construction « intrinsèque » de la courbe fractale peut être ainsi faite. On se place sur Fn. On a seulement besoin de connaître le changement de direction de chaque segment élémentaire de longueur q-n de l'étape suivante. Sur le générateur fractal F1, ces angles ont été nommés αi. Le problème est maintenant de trouver α(s).
. Une construction « intrinsèque » de la courbe fractale peut être ainsi faite. On se place sur Fn. On a seulement besoin de connaître le changement de direction de chaque segment élémentaire de longueur q-n de l'étape suivante. Sur le générateur fractal F1, ces angles ont été nommés αi. Le problème est maintenant de trouver α(s).
Les points de Fn qui sont communs avec f, sont caractérisés par des paramètres rationnels s et décrits avec n figures dans la base de comptage p, ![]() . Il dénote sk, le dernier chiffre non nul de s, c'est-à-dire que
. Il dénote sk, le dernier chiffre non nul de s, c'est-à-dire que
![]() .
.
Il est facile de vérifier, prouvé par ![]() que l'angle relatif entre le segment numéro s.pn – 1 et le segment numéro s.pn sur Fn est donné par :
que l'angle relatif entre le segment numéro s.pn – 1 et le segment numéro s.pn sur Fn est donné par :
![]() .
.
Cette formule définit COMPLETEMENT la fractale par un chemin très simple, uniquement par la (p – 1) structure des angles αi, et indépendamment du système de coordonnées particuliers dans le plan (x, y).
On peut finir cette partie en considérant une autre généralisation de la construction des fractales. La courbe de Van Koch est discontinue dans les échelles à cause de la discrétisation de la méthode qui consiste à appliquer des générateurs. La continuité de la construction peut être retrouvée en introduisant des pas immédiats entre Fn et Fn + 1. On définit un sous niveau de fractalisation k, tel que ![]() , et on généralise
, et on généralise ![]() dans le chemin suivant : en se plaçant seulement sur Fn, si sn = 0 alors
dans le chemin suivant : en se plaçant seulement sur Fn, si sn = 0 alors ![]() , tandis que si sn ≠ 0 alors
, tandis que si sn ≠ 0 alors ![]() . La courbe fractale est dessinée dans les termes de la variable de l'espace x et de la variable d'échelle ln(δx).
. La courbe fractale est dessinée dans les termes de la variable de l'espace x et de la variable d'échelle ln(δx).
5.2.2.3.3.2. Les courbes fractales dans l'espace
Dans IR3, la rotation d'opérateurs complexes est simplement remplacée par une matrice de rotation en trois dimensions Rk. Le générateur F0 est défini par les coordonnées des p points, Uk = (Xk, Yk, Zk) et le point du paramètre s sera défini par le vecteur :
![]() .
.
Dans le même chemin, si on lui donne la matrice de rotation relative Ak sur le générateur, l'équation intrinsèque de la fractale est donnée par la dernière figure (de rang h) non nulle de la s-expansion :
![]() .
.
Une intéressante particularité de la sous-classe d'une telle fractale est la classe de courbes de dimension fractale 2, puisque comme ce sera vu dans une prochaine section, c'est la dimension fractale universelle des trajectoires des particules en mécanique quantique. Ils sont construits par p = q2 segments de longueurs ![]() , dans le cas d'une parfaite auto-similarité. Le cas des générateurs orthogonaux dans IR3 est particulièrement simple. Par exemple, avec q = 3, et p = 9, on peut construire entre autres, les générateurs suivants :
, dans le cas d'une parfaite auto-similarité. Le cas des générateurs orthogonaux dans IR3 est particulièrement simple. Par exemple, avec q = 3, et p = 9, on peut construire entre autres, les générateurs suivants :
![]() (Nottale, 1993)
(Nottale, 1993)
ou encore q = 4, et p = 16,
![]() (Nottale, 1993)
(Nottale, 1993)
etc.
5.2.2.3.3.3. Les surfaces fractales
Bien que l'étude des courbes fractales soit maintenant instructive pour comprendre les propriétés des espaces fractals - puisque les lignes géodésiques des espaces fractals et des espaces-temps sont des courbes fractales particulières - des problèmes plus spécifiques pour les espaces (comme comparer des fonctions ou des applications) commencent à être rencontrés quand on étudie les surfaces (c'est-à-dire les fractales de dimension deux). On illustrera ce point après une étude préliminaire d'une classe particulière des surfaces fractales faites des côtés orthogonaux.
tyle='font-family: Times New Roman;'>En essayant d'obtenir un premier membre de cette classe par une généralisation à deux dimensions du bien-fondé de la courbe fractale constituée par F0 qui est un carré de côté 1, on obtient le générateur F1 fait de 48 nouveaux carrés de longueur ![]() . Si on veut maintenant construire F2 par la méthode de « fractalisation » usuelle, c'est-à-dire en remplaçant chacun des 48 carrés par une version d'échelle de F1, une nouvelle et spécifique difficulté apparaît en égalant les structures à leur limite. Alors que F1 peut lui être égal quand il n'y a pas de rotation d'une face sur une face adjacente, ce n'est pas plus long par rapport au le cas où la rotation relative est
. Si on veut maintenant construire F2 par la méthode de « fractalisation » usuelle, c'est-à-dire en remplaçant chacun des 48 carrés par une version d'échelle de F1, une nouvelle et spécifique difficulté apparaît en égalant les structures à leur limite. Alors que F1 peut lui être égal quand il n'y a pas de rotation d'une face sur une face adjacente, ce n'est pas plus long par rapport au le cas où la rotation relative est ![]() . Désormais, une complète description d'une telle fractale implique non seulement l'offre d'un générateur, mais aussi de plusieurs égalités d'état d'un côté à l'autre. Plus généralement, un générateur de ce type peut être construit en lui donnant, dans un système de coordonnées cartésiens (x, y, z), la hauteur Zij (i = 0 à q – 1 ; j = 0 à q – 1) de la face horizontale dans F1. Alors le nombre total des faces est :
. Désormais, une complète description d'une telle fractale implique non seulement l'offre d'un générateur, mais aussi de plusieurs égalités d'état d'un côté à l'autre. Plus généralement, un générateur de ce type peut être construit en lui donnant, dans un système de coordonnées cartésiens (x, y, z), la hauteur Zij (i = 0 à q – 1 ; j = 0 à q – 1) de la face horizontale dans F1. Alors le nombre total des faces est :
![]() .
.
Si ce nombre est conservé quels que soient les connections, la dimension fractale est ![]() . On note qu'il y aurait un terme d'addition si F1 contenait des faces d'embranchement retardées dans lesquels cas le nombre de faces horizontales serait plus large que q2.
. On note qu'il y aurait un terme d'addition si F1 contenait des faces d'embranchement retardées dans lesquels cas le nombre de faces horizontales serait plus large que q2.

5.2.2.3.3.4. Les fonctions fractales
5.2.2.3.3.4.1. La construction mathématique
Tout commence avec le théorème de Lebesgue énoncé en 1903, « une courbe de longueur finie est presque partout différentiable ». Ce théorème a pour corollaire : « une courbe continue et non différentiable presque partout entre deux points est explicitement dépendante d'échelle, mais sa longueur reste souvent bornée lorsque l'intervalle d'échelle tend vers zéro ». D'où le théorème fondamental suivant, démontré par Laurent Nottale : une courbe continue et non différentiable partout est explicitement dépendante d'échelle et sa longueur tend vers l'infini lorsque l'intervalle tend vers zéro.
5.2.2.3.3.4.2. La dimension fractale d'une courbe
Lest une fonction de dimension fractale D qui diverge comme 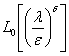
![]()
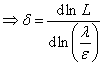 . Il faut remarquer que si
. Il faut remarquer que si ![]() , la résolution sur L,
, la résolution sur L, ![]() .
.
5.2.2.3.3.4.3. Les fonctions fractales
Une fonction fractale est une famille de fonctions dépendant d'un paramètre ε = δy représentant les résolutions sur y, modulo une relation d'équivalence ε1.
Soit ![]() .
.
![]()
et vérifiant
![]()
où ![]() est une fonction de lissage. Cette relation indique que la fonction à résolution ε est une version lissée de la même fonction à la résolution η.
est une fonction de lissage. Cette relation indique que la fonction à résolution ε est une version lissée de la même fonction à la résolution η.
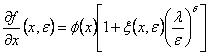 avec la moyenne
avec la moyenne ![]()
Chaque fonction de cette famille est différentiable si ε ≠ 0. Seule la fonction fractale limite f(x, 0) est non différentiable.
Si on néglige la fluctuation résiduelle ξ – 1, est une solution d'une équation du groupe de renormalisation :
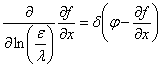
où δ est une dimension anormale. Comment cette dimension anormale δ est-elle reliée à la dimension fractale D ? La réponse dépend de la variable à laquelle est reliée la résolution ε : x ou y. Alors, on a besoin de savoir d'abord la relation entre δx et δy sur une fonction fractale.
L'élément différentiel d'une fractale de dimension D peut être écrite comme ![]() , c'est-à-dire comme la relation cherchée entre δx et δy est :
, c'est-à-dire comme la relation cherchée entre δx et δy est :
![]() .
.
Dès que δy >> δx, l'élément différentiel sur le fractal devient ![]() . La longueur totale diverge comme
. La longueur totale diverge comme ![]() , et on obtient finalement la relation ci-dessus.
, et on obtient finalement la relation ci-dessus.
On suppose maintenant que ε = δy. La dimension anormale est reliée à la dimension fractale par :
![]()
On suppose maintenant que ε n'est plus égale à δy, mais à δx, soit ε = δx.
![]() .
.
δx et δy sont reliés par la relation ![]() où D est la dimension fractale.
où D est la dimension fractale.
![]()
En conclusion et plus généralement, la dimension d'échelle δ est reliée aux dimensions fractale D et topologique DT par :
![]() ,
,
ou
![]() .
.
Ces deux définitions rappellent qu'il n'y a pas d'échelles absolues dans la nature. Seul un rapport d'échelle entre deux systèmes a un sens. Il existe une dépendance d'échelle explicite dans de nombreux domaines de la physique, mais aussi dans biens d'autres sciences comme la géographie où cette évidence est défendue depuis longtemps. De plus, ces définitions permettent, en abandonnant la différentiabilité, de conserver la continuité. Cependant, elles ne prennent un sens fort que si on les rapproche du principe de relativité.
On peut noter un théorème à propos de ξ. En effet, une définition complète dans laquelle sera donnée la dimension fractale de la dérivée renormalisée d'une fonction fractale qui est formellement infinie. Cela signifie que :
![]() ,
,
avec ζ fini et ε = δx, si δ = 1 alors D = ∞ pour la formule précédente. Ce résultat influencera énormément les dérivées suivantes. Autrement dit, quelle que soit la valeur de ε, ξ ne disparaît pas puisque ![]() – et est alternativement positive et négative – et que la pente est finalement proportionnelle à ε-1.
– et est alternativement positive et négative – et que la pente est finalement proportionnelle à ε-1.
Une autre propriété de ξ peut être obtenue par une intégration de 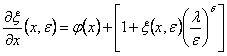 . Pour l'hypothèse que f est finie, on conclut que
. Pour l'hypothèse que f est finie, on conclut que ![]() est elle aussi finie, et que l'intégrale de ξ a disparu comme εδ, contrairement à l'intégrale de
est elle aussi finie, et que l'intégrale de ξ a disparu comme εδ, contrairement à l'intégrale de ![]() laquelle est finie et non nulle.
laquelle est finie et non nulle.
5.2.2.3.3.5. Qu'est-ce qu'une dimension fractale ?
Pour achever la définition progressive du concept de dimension fractale, on peut affirmer que deux approches sont possibles dans l'espace à, au moins, trois dimensions :
(1) l'approche de Benoît Mandelbrot. D est une dimension fractale constante définit telle que δ = D – DT où ![]() . Il s'agit de la définition d'un objet fractal ;
. Il s'agit de la définition d'un objet fractal ;
(2) l'approche de Laurent Nottale. δ devient variable ; c'est ce qu'il appelle la dimension d'échelle. ![]() , où δ est appelé djinn (ou dimension d'échelle variable). Il s'agit de la définition d'un espace fractal.
, où δ est appelé djinn (ou dimension d'échelle variable). Il s'agit de la définition d'un espace fractal.
Enfin, il faut préciser que le terme dimension est ambigu. En effet, il possède deux définitions :
(1) lorsque l'on parle de la dimension de l'espace, on évoque l'espace à trois dimensions ;
(2) lorsque l'on évoque une dimension de l'espace, on évoque un vecteur particulier ; c'est dans ce sens que doit être comprise la dimension d'échelle.
5.2.2.3.3.6. La dimension fractale variable
On introduit une généralisation simple de la courbe de Van Koch qui peut avoir une dimension fractale entre 1 et 2, qui est basée sur un générateur qui dépend d'un paramètre angulaire β.
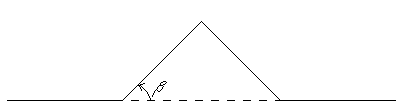
Le paramètre q est donnée par :
q = 2(1 + cos β).
La dimension fractale est :
![]()
et
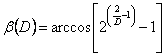 .
.
Maintenant, on peut construire une fractale à dimension variable en généralisant l'équation ![]() :
:
![]() .
.
5.2.2.3.3.7. Vers la définition d'un espace-temps fractal
Avant d'étudier plus en détail le concept d'espace fractal, on doit chercher à établir une relation plus précise entre non différentiabilité et fractalité. On démontre que continuité et non différentiabilité impliquent une dépendance d'échelle. On considère une fonction continue f(x) entre deux points A0(x0, f(x0)) et AΩ(xΩ, f(xΩ)). Puisque f est non différentiable, il existe un point A1 de coordonnées (x1, f(x1)) avec x0 < x1 < xΩ, tel que A1 n'est pas sur le segment A0AΩ. Alors la longueur totale L1 = L(A0A1) + L(A1AΩ) > L0 = L(A0AΩ). Maintenant, on peut itérer l'argument et trouver deux coordonnées x01 et x11 avec x0 < x01 < x1 et x1 < x11 < xΩ, tel que L2 = L(A0A01) + L(A01A1) + L(A1A11) + L(A11AΩ) > L1 > L0. En itérant, on construit finalement des approximations successives f0, f1, …, fn de f(x) qui ont des longueurs L0, L1, …, Ln qui croissent avec la résolution.
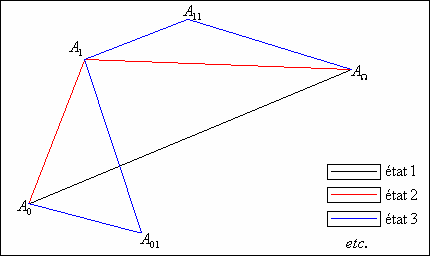
5.2.3. La théorie de la relativité d'échelle de Laurent Nottale
La théorie de la relativité d'échelle est construite autour des trois principes : le principe de relativité, le principe de covariance et le principe d'équivalence.
5.2.3.1. Le principe de la relativité
Avec Laurent Nottale, le « principe d'échelle » de Benoît Mandelbrot est identifié au grand principe physique de la relativité, ce qui aboutit à la définition d'une relativité d'échelle. La relativité d'échelle généralise l'application des fractales. Les lois de la nature doivent être valides quel que soit le système de coordonnées choisi. Un système de coordonnées est défini par une liste de nombres, ces nombres représentant les valeurs de grandeurs qui caractérisent l'état du système de coordonnées. Elles sont relatives à un autre système de coordonnées. Ce principe est extrêmement fort : une loi transcrivant un phénomène naturel observé ne doit pas dépendre du support, de l'espace support choisi. Il dépasse donc naturellement, presque lui-même le cadre de la seule physique.
En géographie, cela fait une cinquantaine d'années que nous recherchons des lois spatiales, mélangeant les aspects naturels et les aspects anthropiques. Malheureusement, la dépendance de nos lois par rapport au système de coordonnées choisi est évidente. En introduisant le principe de relativité dans notre discipline, le sens de nos mesures et interprétations ne pourra qu'être plus fort.
En fait, il existe « trois grandes relativités » : la relativité galiléenne, la relativité restreinte et la relativité générale. Chacune de ces relativités définit une relativité du mouvement. À ces relativités du mouvement, l'idée de Laurent Nottale est de définir une relativité d'échelle qui portera le nom de relativité galiléenne d'échelle, relativité restreinte d'échelle et relativité générale d'échelle. Ce travail n'exposera que la relativité d'échelle galiléenne qui explique les cas où la dimension fractale varie peu dans l'espace-temps, et la relativité restreinte d'échelle qui explique certains cas de multifractalité. La relativité générale d'échelle ne sera qu'évoquer car les travaux ne sont qu'à leur début. De plus, ce sujet passionnant ne concernera sans doute pas l'espace géographique dans la mesure où il représente un espace-temps localement plat. La relativité restreinte devrait donc amplement suffire pour le décrire.
La relativité d'échelle est une représentation géométrique de la nature, par l'intermédiaire d'un espace, et non plus un objet ! L'objet est ponctuel et peu commode à généraliser. Un espace est plus pratique car il est défini de l'intérieur, donc descriptible en tout point.
5.2.3.1.1. La relativité galiléenne
C'est une première forme de relativité. Elle consiste à séparer espace et temps. La position devient une conséquence du temps dans le cadre d'un déplacement. Elle est à la base de la mécanique newtonienne dont le fer de lance est le principe d'inertie. Relativités restreinte et générale montrent que ce n'est qu'un cas particulier, qu'une première approximation.
5.2.3.1.2. La relativité restreinte
La relativité restreinte change de cadre théorique par rapport à la relativité galiléenne. En effet, on ne sépare plus désormais l'espace et le temps, mais on construit un espace-temps (à quatre dimensions) plat (c'est-à-dire non courbe). La construction de la théorie n'est possible que si l'on pose l'invariance de la vitesse de la lumière qui devient donc la vitesse maximale de propagation des interactions. De plus, chaque référentiel possède, pour les distinguer, un temps propre, c'est-à-dire le temps indiqué sur l'horloge liée à ce référentiel. Un changement de référentiel s'opère grâce à la transformation de Lorentz, c'est-à-dire une rotation dans l'espace-temps.
5.2.3.1.3. La relativité générale
La différence entre la relativité restreinte et la relativité générale peut paraître minime. Toutefois, elle modifie profondément les équations de la physique par le simple fait de ne plus avoir un espace-temps plat, mais courbe. Aussi, pour y remédier, Albert Einstein introduisit les principes de covariance et d'équivalence qui montrent, entre autres, que la matière équivaut à la géométrie intrinsèque (Nottale, 1998, p. 83).
5.2.3.2. Les principes de covariance et d'équivalence
Le principe de covariance exige que les équations doivent garder leur forme (la plus simple possible) dans les transformations d'un système donné de coordonnées. On distingue deux types de covariance : la covariance faible et la covariance forte. La covariance faible correspond au cas où les équations ont gardé, sous une transformation plus générale, la même forme que sous la transformation particulière précédente. La covariance forte correspond au cas où la forme la plus simple possible des équations a été obtenue.
Le principe d'équivalence articule les principes de relativité et de covariance pour un « objet » donné. Il montre comment un objet peut être remplacé, dans des conditions bien précises, par un autre équivalent.
5.2.4. La dimension fractale constante ou la relativité d'échelle galiléenne
Les fractales à dimension constante correspondent à la relativité galiléenne. On peut en présenter deux types : le modèle puissance pur et le modèle avec une correction log-périodique.
5.2.4.1. Les régressions linéaires ou la relativité d'échelle galiléenne
Il s'agit d'un cas particulier des dilatations globales d'échelle. Il n'existe qu'une seule variable d'échelle et une dimension fractale constante (Mandelbrot, 1975 ; 1997). L'invariance d'échelle n'est qu'un cas très particulier de dépendance d'échelle. En physique, elle correspond au cas galiléen des lois de la relativité restreinte d'échelle.
Les lois de puissance rencontrées dans les comportements fractals auto-similaires peuvent être identifiées comme les plus simples des lois recherchées. Elles correspondent à la plus simple des équations d'échelle possible, qui s'écrit comme une équation aux valeurs propres de l'opérateur de dilatation : ĎL = bL. « L'auto-similarité est une sorte d'inertie d'échelle » (Nottale, 1998, p. 224). La solution est une loi fractale standard divergente :
![]() où
où ![]() avec D constant.
avec D constant.
δ est la dimension d'échelle définie par Benoît Mandelbrot. D est la dimension fractale. DT est la dimension topologique de l'ensemble fractal (objet ou espace). λ et L0 sont des grandeurs qui a-dimensionnent L et ε. λ est appelée échelle de coupure. L0 est la valeur initiale.
En fait, δ correspond à un nombre qui caractérise l'accroissement de L avec ε :
![]() .
.
Sous une dilatation (ou une contraction) apparaît la structure galiléenne du groupe de transformations d'échelle. On transforme ε en ε' :
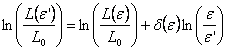
![]()
Plus généralement, une transformation globale ρ (dilatation ou contraction globale) décrite au sein de « l'espace » mathématique appelé « espace des échelles » s'écrit comme le rapport de deux états d'échelle :
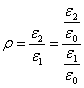
![]()
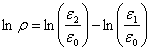
La structure mathématique est donc comparable à celle des vitesses pour le mouvement (fig. 24) :
x' = x + vt avec t = t'.
La composition de deux dilatations ε, ε' et ε'' s'exprime de la manière suivante :
![]()
![]() .
.
Elle ressemble à v'' = v' + v avec ![]() , qui est la loi de « composition des vitesses » du groupe de Galilée.
, qui est la loi de « composition des vitesses » du groupe de Galilée.
| Loi du mouvement | Loi d'échelle |
|---|---|
| x : position du point de vue des déplacements | ln L : position du point de vue des changements d'échelle |
| t : mesure du mouvement | δ : mesure des changements d'échelle (ou djinn) |
| v : état du mouvement | ln ε : état d'échelle |
5.2.4.1.1. Une brisure de la symétrie d'échelle (ou l'apparition de la dépendance d'échelle)
Soit un espace-temps continu, mais non nécessairement différentiable. Les coordonnées curvilignes que l'on peut définir dans cet espace-temps dépendent explicitement des résolutions spatio-temporelles, L = L(ln ε).
On suppose que dans l'espace des (ln ε, L) soit solution de l'équation différentielle, que l'on suppose être du premier ordre en première approximation
![]() où L est inconnue.
où L est inconnue.
Pour L variant peu autour d'une valeur constante, on peut faire un développement perturbatif du type β(L) = a + bL ; l'équation précédente devient :
![]()
ce qui se résout en :
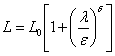
où L0 est une solution particulière (le générateur) et δ = –b. λ est une sorte de dimension caractéristique du cadre dans lequel on effectue les mesures c'est-à-dire une échelle de coupure. ε symbolise les résolutions. Cette solution présente deux comportements asymptotiques particuliers :
pour les micro échelles, si δ > 0, la dépendance d'échelle de L est une loi puissance
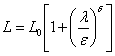 ;
;pour les méso échelles, il n'y a pas de dépendance d'échelle :
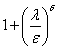 devient négligeable ;
devient négligeable ;pour les macro échelles, si δ < 0, la dépendance d'échelle de L est une loi puissance
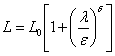 .
.
5.2.4.1.2. La brisure de l'invariance d'échelle : les échelles de transition
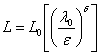 est la forme classique de l'invariance d'échelle qui se différencie de la dépendance d'échelle générale par l'absence du « + 1 ». Cette invariance est spontanément brisée par l'existence d'une dynamique. Si on change l'origine du système de coordonnées, on obtient :
est la forme classique de l'invariance d'échelle qui se différencie de la dépendance d'échelle générale par l'absence du « + 1 ». Cette invariance est spontanément brisée par l'existence d'une dynamique. Si on change l'origine du système de coordonnées, on obtient :
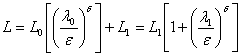 où
où 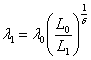 .
.
Cette équation en physique satisfait au double principe de relativité du mouvement et d'échelle. C'est la solution de la plus simple équation différentielle en échelle que l'on puisse écrire (équation du premier ordre ne dépendant que de L lui-même). L'avantage de ce raisonnement est qu'il est reproductible. Le développement en série limitée de Taylor se poursuit par un polynôme du second degré, puis du troisième, etc.
![]() (Développement en série limitée de Taylor).
(Développement en série limitée de Taylor).
Autrement dit, si l'on pousse plus loin le développement limité, on obtient des solutions montrant plusieurs échelles de transition, en accord avec le comportement observé de nombreux objets fractals naturels.
5.2.4.2. La correction log-périodique, un exemple de régression non linéaire
L'invariance d'échelle est caractérisée par des lois puissances. Parmi les corrections apportées à l'invariance d'échelle, la plus efficace et la plus courante dans de nombreux cas est la correction de la loi puissance par une loi log-périodique, qui est définie par l'apparition de dimensions fractales complexes. Un des avantages de la correction log-périodique est que la dimension fractale, bien que complexe, reste constante.
5.2.4.2.1. Les lois d'échelles non linéaire : les équations du deuxième ordre et les dimensions fractales complexes
5.2.4.2.1.1. La correction log-périodique et l'invariance d'échelle
Didier Sornette (2000, 2003) a essayé de modéliser l'oscillation observée en utilisant une dimension fractale complexe. Rappelons qu'un nombre complexe est un nombre z tel que z = a + ib, où a est appelé la partie réelle et ib la partie imaginaire avec i2 = –1 (Murray, 1992). Ainsi arrive-t-on à modéliser cette oscillation en utilisant la forme trigonométrique des nombres complexes.
En effet,
![]()
La partie réelle est
![]() .
.
Elle correspond à une fluctuation log-périodique. Il faut remarquer qu'il est très courant dans des sciences, comme la physique, d'utiliser les nombres complexes pour ensuite revenir aux nombres réels, ce qui, d'un point de vue analytique, est correct puisque les nombres complexes sont une « extension » des nombres réels. Cette partie réelle correspondant à une fluctuation log-périodique de l'invariance d'échelle.
5.2.4.2.1.2. La correction log-périodique et la dépendance d'échelle
Si l'on revient à la théorie de la relativité d'échelle, il faut trouver une équation différentielle d'échelle donnant cette fluctuation log-périodique. La démonstration est plus compliquée que celle de l'invariance d'échelle, mais elle aura pour effet de satisfaire au principe de covariance : la dépendance d'échelle log-périodique aura la même forme mathématique, mais plus sophistiquée, que la dépendance d'échelle puissance.
Avant de poursuivre le raisonnement, il faut opérer un changement de variable et poser : 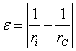 , où
, où ![]() correspond à ce que l'on appelle la valeur critique de manière générale, et dans le cas des lois rang-taille, on appellera cette valeur le rang critique.
correspond à ce que l'on appelle la valeur critique de manière générale, et dans le cas des lois rang-taille, on appellera cette valeur le rang critique.
Pour obtenir une telle fluctuation, il faut reprendre l'équation de l'invariance d'échelle :
![]() .
.
On exige que cette équation ne soit plus égale à zéro :
![]() .
.
Cependant, en vertu du principe de covariance, on exige que ![]() corresponde à une équation différentielle de la même forme que l'équation de l'invariance d'échelle.
corresponde à une équation différentielle de la même forme que l'équation de l'invariance d'échelle.
On obtient donc :
![]()
où D' = D + iω.
Toutefois, D' correspond à une dimension fractale complexe. Pour trouver V(ε), il faut dériver par le logarithme de la résolution l'équation ![]() , ce qui donne :
, ce qui donne :
![]() .
.
Dans l'équation (19), on remplace ![]() par sa valeur
par sa valeur ![]() , ce qui correspond, finalement à une équation différentielle du second ordre :
, ce qui correspond, finalement à une équation différentielle du second ordre :
![]() .
.
L'équation précédente se résout très facilement car elle correspond à un modèle d'équation différentielle connu dont la solution est :
![]()
où δ = iω.
En posant l'équation précédente sous sa forme trigonométrique, on obtient :
![]() .
.
Dans cette équation, on exige, tout comme dans le paragraphe précédent, que la partie imaginaire soit négligeable, et on obtient la correction log-périodique dépendante d'échelle :
![]() .
.
Autrement dit, le simple fait d'avoir un « + 1 » supplémentaire par rapport à la formule de Didier Sornette suffit à la transformer en une relation dépendante d'échelle et obtenir une équation plus pratique.
Toutefois, la fonction log-périodique est une fonction à quatre paramètres. Deux sont facilement paramétrables : la dimension fractale D et a qui correspond à l'ordonnée à l'origine de la courbe à ajuster, c'est-à-dire la valeur initiale. b et ω restent à identifier. En conclusion, bien que non linéaire, dans cette fonction, la dimension fractale reste constante. La log-périodicité n'est qu'une correction qui améliore nettement la loi puissance trouvée initialement.
5.2.4.2.2. Discrétisation de loi log-périodique
En théorie, la log-périodicité ![]() est parfaitement continue. En pratique, il faut discrétiser les données autour de la valeur critique.
est parfaitement continue. En pratique, il faut discrétiser les données autour de la valeur critique.
Ainsi la discrétisation des lois log-périodiques a été utilisée, entre autres, par Laurent Nottale (et alii, 2000) sous la forme d'une relation de récurrence :
le='font-family: Times New Roman;'>![]() .
.
Cette approche est intéressante dans la mesure où VC et g sont des paramètres assez simples à estimer. VC est ce que l'on appelle la valeur critique. Il s'agit d'une valeur vers laquelle converge ou diverge la série. Il n'y a pas vraiment de condition sur VC, si ce n'est que cette valeur doit être choisie à l'extérieur de la série des données. g est, par contre, un rapport d'échelle constant qui permet de lier toutes les données. On peut estimer g et TC de la manière suivante :
![]() ;
;
![]() .
.
Il faut noter qu'il existe de nombreuses autres formules équivalentes à ces deux formules.
Pour l'instant, cette méthode n'a été appliquée qu'à des séries chronologiques. La valeur critique sera ici un temps critique (qui est l'équivalent d'un rang). Toutefois, on pourrait imaginer appliquer cette méthode à un ordre spatial, ce qui est bien sûr plus compliqué. En effet, le temps n'a qu'une dimension tandis que l'espace géographique en a au minimum deux.
5.2.5. Les fractales à dimension variable (ou djinn)
Il s'agit ici de montrer que « l'horreur multifractale » n'est pas forcément nécessaire à travers les lois d'échelle où la dimension fractale devient variable.
5.2.5.1. Les lois d'échelle, le djinn et le formalisme lagrangien
Dans une relativité non galiléenne, δ n'a aucune raison de rester constante. Cette variable joue exactement le même rôle que la variable t dans les lois du mouvement. Il s'agit de comprendre le cas de la dynamique d'échelle. La dimension d'échelle δ devient une variable primaire, traitée sur le même plan que l'espace et le temps. Les résolutions sont définies comme dérivées à partir de la coordonnée fractale et δ, c'est-à-dire comme s'il s'agissait de « vitesses d'échelle ». À partir des variables δ et ln L (t et x par analogie), on peut construire tout naturellement une grandeur qui jouera le rôle de la vitesse :
![]() .
.
Ce sens nouveau et fondamentale donné à la dimension d'échelle, traitée maintenant comme une variable, rend nécessaire de lui attribuer un nouveau nom : le djinn. Il faut noter que l'emploie de ce terme permet de contracter l'expression « dimension fractale variable ». Il s'agit de travailler dans un espace-temps-djinn à cinq dimensions. Le caractère vectoriel des zooms est alors apparent, car les quatre résolutions spatio-temporelles peuvent se définir à partir des quatre coordonnées d'espace-temps et du djinn :
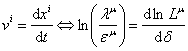 9.
9.
L'accélération d'échelle est un nouveau concept nécessaire au passage à des lois d'échelle non linéaires et à une « dynamique » d'échelle. L'introduction de ce concept permet de renforcer encore l'identification des fractals à dimension constante à une « inertie d'échelle ». L'équation « du vide » en échelle s'écrit, à une dimension, ![]() . Elle s'intègre comme
. Elle s'intègre comme ![]() . Cette constante signifie ici son indépendance en fonction du djinn δ. La solution prend la forme :
. Cette constante signifie ici son indépendance en fonction du djinn δ. La solution prend la forme : ![]() .
.
Plus généralement, on peut faire l'hypothèse que les lois d'échelle peuvent être construites à partir d'un principe de moindre action. On introduit une fonction de Lagrange d'échelle L ![]() , où
, où ![]() . Comme pour les lois du mouvement, on peut postuler l'existence d'un lagrangien L
. Comme pour les lois du mouvement, on peut postuler l'existence d'un lagrangien L![]() . À partir de ce lagrangien, on peut construire une action :
. À partir de ce lagrangien, on peut construire une action :
![]()
et obtenir une équation d'Euler-Lagrange à partir d'un principe d'action stationnaire. Le principe d'action stationnaire conduit alors à des équations d'Euler-Lagrange d'échelle :
![]() .
.
L'avantage de cette formalisation est qu'elle est beaucoup plus générale et plus simple que celle de la multifractalité.
5.2.5.2. La dynamique d'échelle et la force d'échelle
Toujours en poursuivant l'analogie avec les lois du mouvement, on peut approfondir le concept de force d'échelle. En effet, l'introduction d'une force d'échelle permet d'écrire une version appliquée aux lois d'échelle de l'équation de la dynamique d'Isaac Newton :
![]()
ou
 .
.
μ est une « masse d'échelle », qui mesure comment le système résiste à la force d'échelle.
La force d'échelle constante dérive d'un « potentiel d'échelle » défini tel que :
![]() .
.
On peut écrire 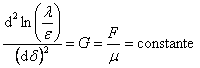 . Il s'agit là de l'équivalent pour les échelles de ce qu'est la chute des corps en gravité constante. Sa solution est un comportement parabolique :
. Il s'agit là de l'équivalent pour les échelles de ce qu'est la chute des corps en gravité constante. Sa solution est un comportement parabolique :
![]() ;
;
![]() .
.
Après redéfinition des constantes d'intégration, cette solution s'exprime de nouveau sous la forme :
![]() ;
;
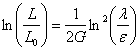 .
.
Ainsi la dimension fractale, ordinairement constante, est devenue une fonction linéaire de la log-résolution, et le logarithme de la longueur varie maintenant, non plus linéairement, mais de manière parabolique.
« Il est fréquent qu'après analyse soigneuse de la dépendance d'échelle d'une grandeur, le modèle en loi puissance soit rejeté pour cause de variation de la pente dans le plan (log L, log ε). Dans de tels cas, la conclusion que le phénomène considéré n'est pas fractal pourrait s'avérer prématurée. Il s'agit au contraire s'agir d'un comportement fractal non linéaire relevant d'une dynamique d'échelle, auquel cas l'identification et l'étude de la force d'échelle responsable de la distorsion se révèlerait du plus haut intérêt » (Nottale, 2002a).
5.2.6. La relativité d'échelle restreinte
Le principe de relativité des référentiels galiléens et de celui de l'invariance d'une certaine résolution forment ensembles une relativité restreinte d'échelle. En physique, il demeure assez « simple » de deviner une telle échelle, mais, en géographie, il n'est pas sûr que l'on arrive à en définir une. Pourtant, la géographie rencontre des cas où la dimension fractale devient variable. C'est donc avec la relativité restreinte que le concept d'« espace-temps-djinn » prend tout son sens. Elle n'a été développée qu'à deux dimensions, une dimension d'espace-temps et le djinn. Un traitement complet à cinq dimensions reste à réaliser. Tout part de l'idée que les lois fractales standard à dimension fractale constante ont la structure du groupe de Galilée. Cependant, ce groupe n'est qu'un cas très particulier et dégénéré du groupe de Lorenz.
De plus, avec la relativité d'échelle restreinte, la dimension fractale tend maintenant vers l'infini quand l'intervalle de résolution tend vers une échelle microscopique. En allant à des résolutions de plus en plus petites, la dimension fractale passera donc successivement par les valeurs 2, 3, 4, ce qui permettrait de couvrir une surface, puis l'espace, puis l'espace-temps à l'aide d'une unique coordonnée. Il est donc possible de définir un espace-temps plat nécessitant, dans les repères fractals adéquats, seulement deux dimensions aux très petites échelles. En allant vers les grandes résolutions, l'espace-temps-djinn voit sa cinquième dimension varier de moins en moins vite pour devenir presque constante aux échelles accessibles, qui s'identifie à la transition fractal – non fractal dans le référentiel de repos.
5.2.7. La relativité d'échelle généralisée
Le champ d'échelle correspond à une distorsion dans l'espace des échelles par rapport aux lois auto-similaires usuelles, ce qui peut également être représenté en termes d'espace d'échelle courbe. Cependant, la théorie reste à construire.
5.2.8. L'équation d'Erwin Schrödinger généralisée et une dynamique induite de type quantique
5.2.8.1. La définition de la mécanique quantique (Messiah, 1959 ; Cohen-Tannoudji et alii, 1977 ; Landau, Lifchitz, 1989 ; Gribbin, 1994)
« La mécanique quantique est l'ensemble des lois nécessaires à la prévision du mouvement des objets microscopiques » (Sapoval, 1997, p. 18). Les fondateurs sont Werner Heisenberg pour la théorie des matrices et Erwin Schrödinger pour la mécanique ondulatoire. La théorie d'Heisenberg est une théorie basée sur la discontinuité. Il s'agit d'un modèle discret. Elle reçut le prix Nobel de physique en 1925. La théorie de Schrödinger est une théorie basée sur la continuité. Il découvrit ce que l'on appelle l'équation de propagation de la fonction d'onde représentant un système quantique donnée, plus connue sous le nom d'équation de Schrödinger. De plus, il démontra que la mécanique des matrices et mécanique ondulatoire étaient équivalentes, ce qui valut à Schrödinger le prix Nobel de physique en 1926. La théorie quantique était née. Cependant, il lui manquait quelque chose : des principes de fonctionnement.
La théorie quantique est une théorie fondée sur des axiomes qui, jusqu'à présent, n'ont pas été démontrés. Laurent Nottale a réussi à le faire en utilisant le principe de relativité et sa théorie de la relativité d'échelle. Il a montré qu'à une certaine échelle de coupure, dans le cas de la physique l'échelle de Planck, tout système, quel qu'il soit, devient quantique ! Les règles de la mécanique quantique seraient-elles universelles ? Les quelques travaux de Laurent Nottale avec le paléontologue Jean Chaline et l'économiste Pierre Grou (2000) tendent à être des indices de cette généralisation méthodologique. Ainsi, la mécanique quantique ne serait-elle pas la « bonne mécanique » à appliquer en sciences humaines .
5.2.8.2. La mécanique quantique et la relativité d'échelle
Il pourrait « exister dans la nature une fractalité auto-amortie. Les objets fractals seraient « robustes » dans ce sens, et ce serait une des raisons pour lesquelles nous pouvons constater leur existence : les géométries fractales « résisteraient mieux car elles amortiraient les excitations auxquelles elles seraient soumises. Cela constitue un exemple de potentiel d'auto-organisation » (Sapoval, 1997, p. 175) qui peut être identifié à la constante D de l'équation de Schrödinger généralisée que nous allons définir maintenant. Cela va également permettre, plus généralement, de définir la dynamique de l'espace géographique fractale.
Trois conditions minimales permettent de transformer l'équation de la dynamique classique en équation de Schrödinger généralisée (Nottale, 1993).
(1) Il existe un très grand nombre (à la limite, une infinité) de trajectoires potentielles (espace des phases) ; cette condition est une conséquence naturelle de la non différentiabilité de l'espace et de la fractalité de l'espace, dans le cas où les trajectoires peuvent être définies précisément comme géodésiques (droites, courbes diverses) de cet espace.
(2) Chacune de ces trajectoires est une courbe fractale (la dimension D = 2, qui correspond à une perte complète d'information sur les déplacements élémentaires, jouant ici un rôle particulier). Dans le cas d'un espace et ses géodésiques, le caractère fractal de l'espace implique directement celui de ses géodésiques.
(3) Il y a irréversibilité au niveau infinitésimal, c'est-à-dire non invariance dans la réflexion de l'élément différentiel de temps dt → –dt. Cette condition est une conséquence immédiate de l'abandon de l'hypothèse de différentiabilité. L'un des outils fondamentaux qui permettent de gérer la non différentiabilité consiste en la réinterprétation des éléments différentiels comme variables. La coordonnée dans l'espace devient une fonction fractale X(t, dt) et sa vitesse, bien que n'existant plus à la limite dt → 0, se définit maintenant comme une fonction fractale. La nouveauté et qu'il y a deux définitions au lieu d'une, qui se transforment l'une dans l'autre par la réflexion dt → –dt. Le concept de vitesse se dédouble :
![]() ;
;
![]() .
.
La condition (1) conduit à adapter une description de type « fluide »dans laquelle on considèrera le champ de vitesse moyen v[x(t), t] de toutes les trajectoires potentielles.
La condition (2) rappelle que les lois d'échelles satisfont au principe de relativité. Dans le cas le plus simple « galiléen d'échelle », la coordonnée (solution d'une équation différentielle d'échelle) se décomposait sous forme d'un terme classique indépendant d'échelle et d'un terme asymptotiquement fractal. Ceci amène à décomposer les déplacements élémentaires dX = dx + dξ sous forme d'une moyenne indépendante d'échelle, dx = vdt, et d'une fluctuation dξ caractérisée par une loi de comportement fractale, ![]() .
.
La condition (3) a pour conséquence un dédoublement des vitesses
![]()
se décomposent en une composée v non fractale (donc dérivable au sens ordinaire) à laquelle s'ajoute une composante fractale divergente ![]() , nulle en moyenne. La source de ce dédoublement se trouve au niveau de l'espace.
, nulle en moyenne. La source de ce dédoublement se trouve au niveau de l'espace.
Sous l'effet d'une variation de dt, V va, au premier ordre, varier selon une fonction de V seulement, conformément aux lois du groupe de renormalisation :
![]()
c'est-à-dire ![]() par un développement autour de V << 1. La solution de cette équation est V = v + W c'est-à-dire
par un développement autour de V << 1. La solution de cette équation est V = v + W c'est-à-dire 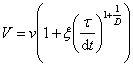 avec
avec ![]() (vitesse moyenne). On pose
(vitesse moyenne). On pose ![]() . τ est l'échelle de transition. ξ est une variable stochastique telle que
. τ est l'échelle de transition. ξ est une variable stochastique telle que ![]() et
et ![]() (fig. 25).
(fig. 25).
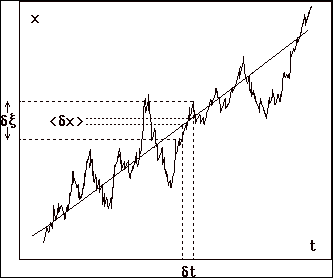
On est amené à introduire un double processus tridimensionnel :
![]() ,
,
dans lequel ![]() avec
avec ![]()
et ![]() ,
,
où dij représente le symbole de Kronecher et D est un paramètre d'échelle fondamental qui caractérise le comportement fractal des trajectoires. Ce n'est rien d'autre qu'une notation différente pour l'échelle de transition fractal – non fractal. Ce paramètre détermine la transition essentielle qui apparaît dans un tel processus entre le comportement fractal à petite échelle (où les fluctuations dominent) et non fractal à grande échelle (où le mouvement classique moyen redevient dominant).
Une représentation naturelle du dédoublement de variables dû à l'irréversibilité consiste en l'utilisation de nombres complexes ; on peut démontrer que ce choix est « covariant », au sens où il préserve la forme des équations. On définit un opérateur complexe de dérivation par rapport au temps, qui porte sur les quantités macroscopiques indépendantes d'échelle, donc dérivables au sens ordinaire,
![]()
puis une vitesse moyenne complexe qui résulte de l'action de cet opérateur sur la variable de position :
![]() .
.
Ainsi, à la limite classique où ![]() , la partie réelle de cette vitesse complexe s'identifie à la vitesse classique tandis que la partie imaginaire disparaît.
, la partie réelle de cette vitesse complexe s'identifie à la vitesse classique tandis que la partie imaginaire disparaît.
Après avoir défini des lois de déplacements élémentaires dans un tel processus fractal et localement irréversible, il faut analyser les effets de ces déplacements sur d'autres grandeurs physiques. On considère une fonction dérivable f(X(t), t). Sa dérivée totale par rapport au temps s'écrit :
![]()
On peut alors calculer les dérivées « avant » et « arrière » de f. Dans ce calcul, la valeur moyenne de ![]() devient
devient ![]() tandis que
tandis que ![]() se réduit à
se réduit à ![]() , si bien que l'équation présente se transforme en un Laplacien en raison de l'équation :
, si bien que l'équation présente se transforme en un Laplacien en raison de l'équation :
![]() .
.
On obtient alors :
![]() .
.
En combinant ces deux dérivées, on obtient l'expression de l'opérateur complexe de dérivation par rapport au temps :
![]() .
.
Il contient deux termes imaginaires supplémentaires, ![]() et
et ![]() , en plus l'opérateur de dérivation totale ordinaire, >
, en plus l'opérateur de dérivation totale ordinaire, >![]() .
.
On peut maintenant réécrire l'équation fondamentale de la dynamique en utilisant cet opérateur de dérivation : celle-ci prendra alors automatiquement en compte les nouveaux effets considérés. Elle garde la forme newtonienne :
![]() , où
, où ![]() est un terme de potentiel.
est un terme de potentiel.
Dans le cas où le potentiel est nul et dans le cas où il s'agit d'un potentiel gravitationnel, cette équation n'est rien d'autre qu'une équation des géodésiques. On a mis en œuvre un principe d'équivalence généralisé, grâce auquel le mouvement (gravitationnel et quantique) reste localement inertiel. Cette équation s'intègre sous la forme de l'équation de Schrödinger.
Plus généralement, on peut reprendre le déroulement de la construction de la mécanique lagrangienne avec ce nouvel outil. Le caractère complexe de la vitesse V implique celui de la fonction de Lagrange, donc l'action S.
La fonction d'onde ψ s'introduit alors très simplement comme une nouvelle expression de cette action complexe :
![]() .
.
Elle est reliée à la vitesse complexe comme suit :
![]() .
.
On peut changer l'outil de description et écrire l'équation d'Euler-Newton en fonction de cette onde :
![]() .
.
Après quelques calculs, cette équation s'intègre sous formed'une équation de Schrödinger généralisée :
![]() .
.
D est une constante d'auto-organisation. Pour retrouver l'équation de la mécanique quantique standard, il suffit de choisir ![]() . L'énigme de l'émergence serait-elle résolue .
. L'énigme de l'émergence serait-elle résolue .
En posant ![]() , on trouve que la partie imaginaire de cette équation est l'équation dite de continuité :
, on trouve que la partie imaginaire de cette équation est l'équation dite de continuité :
![]() .
.
ce qui justifie l'interprétation de ρ comme une densité de probabilité.
5.3. Vers un espace géographique quasi quantique ?
L'espace géographique est-il un espace fractal ? Fonctionne-t-il avec une dynamique quasi quantique ? Avant de répondre à ces questions, il est bon de préciser la non contradiction entre le rapprochement de certains concepts géographiques avec des théories mathématiques. D'abord, l'espace fractal, au sens de Laurent Nottale, présente la particularité d'être indescriptible dans sa totalité. Il est également capable d'englober toutes les échelles géographiques possibles. L'espace géographique peut donc être mathématiquement défini comme étant un espace fractal. De plus, il fonctionne avec une dynamique quasi quantique, c'est-à-dire une dynamique probabiliste (donc possibiliste) qui n'offre donc aucune certitude, mais simplement des cas plus probables que d'autres, qui seront eux aussi définis mathématiquement. Il s'agit ici de dégager quelques conséquences majeures de la définition de l'espace géographique fractal et de sa dynamique quasi quantique induite.
5.3.1. Rôle capital de la transition fractal – non fractal en géographie
La relativité d'échelle éclaire un problème capital que l'on peut rencontrer lorsque l'on étudie un objet géographique par une analyse fractale. D'abord, elle explique la signification de la loi puissance par l'introduction d'une échelle de coupure à partir de laquelle un objet non fractal aux petites échelles, par exemple, devient fractal aux grandes échelles. Cette observation est lourde de conséquences car elle signifie qu'un objet peut parfaitement présenter un aspect non fractal à une échelle donnée pour devenir fractal à une autre échelle. Autrement dit, l'analyse fractale permet d'identifier les « bonnes échelles », les échelles que l'on pourrait nommer « optimale » ! L'archétype, en géographie, demeure la ville. Les différentes analyses menées sur celles-ci (Frankhauser, 1994 ; Tannier, Pumain, 2005) sont peu convaincantes car elles ne prennent pas en compte le fait qu'un objet comme la ville possède des échelles spécifiques dans lesquelles toute sa fractalité se manifeste. Ces études partent d'un postulat qui manifestement est faux, à savoir le fait qu'un objet est soit fractal, soit non fractal. Il faut arrêter d'opposer les deux états, mais bien comprendre qu'ils peuvent se succéder dans une dynamique d'échelle que nous avons identifiée comme étant quantique, ou plus exactement pour la géographie, quasi quantique. Pour une ville, on s'aperçoit que, globalement, elle est parfaitement fractale. Toutefois, localement, à l'échelle d'un îlot, elle devient non fractale. En revanche, il semble logique que, dans le réseau urbain, cette ville devienne également non fractale, alors que le réseau urbain lui l'est. On s'aperçoit alors toute la complexité du raisonnement amené par l'analyse fractale, et du danger de certaines études qui conclut un peu trop vite que cette analyse ne marche pas. Encore une fois, tout dépend des échelles de coupure dans lesquelles la fractalité se manifeste ou ne se manifeste pas.
5.3.2. Dynamique de type quantique en géographie
La dynamique de type classique adaptée aux sciences humaines fut un des échecs du positivisme ou du bourbakisme. Aussi, la dynamique de type quantique semble être mieux adaptée à la théorisation des sciences humaines comme la géographie. En effet, le principe de relativité d'échelle conduit à accepter que l'espace géographique soit quasi-quantique, ce qui permet de conserver un certain degré de liberté. Autrement dit, les partisans de la liberté humaine de la géographie sociale pourraient s'y retrouver puisqu'il s'agit d'une théorie probabiliste.
L'espace géographique est donc « coincé » entre le domaine classique et le domaine quasi quantique. Cependant, il ne faut pas oublier que la fractalité se manifeste à tous les niveaux et qu'il n'est donc pas impossible de trouver dans l'espace géographique une nouvelle structure en échelle. Toutefois, ce qu'enseigne la relativité d'échelle en géographie est qu'il n'existe aucune échelle absolue. On sauvait déjà que l'espace et le temps absolu n'existaient pas (Albert Einstein, Henri Poincaré). Aujourd'hui, avec Laurent Nottale, c'est au tour des échelles.
5.3.3. Le rôle de la constante d'auto-organisation
Enfin, il faut souligner l'importance capitale en géographie de la constante d'auto-organisation de l'équation généralisée de Schrödinger. La modification de cette constante, c'est-à-dire son éventuelle évolution, transforme considérablement l'objet étudié. Il n'existe malheureusement aucun exemple type en géographie. Toutefois, certaines analyses de Laurent Nottale avec Charles Auffray (http://luth2.obspm.fr/~luthier/nottale/) ont montré que la division cellulaire ainsi que la structure même d'une cellule et d'un tissu organique, dépend de la variation de cette constante en fonction d'une « énergie d'échelle ». On pourrait appliquer ce type d'analyse dans l'explication des divisions spatiales des différents Etats actuels dans le monde. Par exemple, il est peut être possible d'utiliser cette possibilité pour le « réseau » urbain local, national ou mondial en considérant que l'équation de Schrödinger définit comme un champ morphogénétique qui a pu avoir différents niveaux d'énergie dans l'histoire et qui se cristallise en des lieux qui sont des sortes de nœuds et correspondent à des villes. Il y aurait donc comme des singularités locales qui phénoménologiquement seraient dissociées. Toutefois, cela nécessiterait une dimension temporelle plus importante qu'elle l'ait aujourd'hui en géographie. C'est ce qu'essaye de dégager l'exemple de « Boves » et de l'espace historique picard.
5.4. Conclusion de la partie
La géographie n'a pas pris toute la mesure de l'approche par les fractales des structures spatiales et de (ou du moins d'une partie de) l'espace géographique : elle a voulu absolument chercher des modèles mathématiques discontinus, alors que le modèle mathématique continu est bien plus puissant. Pourtant, la fondation de la mécanique quantique par Erwin Schrödinger en 1926 aurait dû faire école. Un an plutôt, Werner Heisenberg avait proposé un modèle discret (celui des matrices) pour expliquer la mécanique quantique. En revanche, Erwin Schrödinger, lui, propose un modèle continu qui explique la discrétisation de Werner Heisenberg ! Autrement dit, travailler sur les fractales, c'est travailler sur un espace des échelles continu ! À partir duquel, le modèle discontinu émergera.
Pour conclure cette partie, on peut résumer les relations espace, temps et espace-temps avec les échelles (résolution ou djinn) par les figures 26 et 27.
| L'espace | Le temps | L'espace-temps | ||
|---|---|---|---|---|
| Distance | Angle | |||
| La grandeur primaire | Position | Orientation | Instant | Temps propre |
| La grandeur conservative associée | Impulsion | Moment angulaire | Énergie | Impulsion Énergie Moment angulaire |
| Les types de variables | Vecteur | Vecteur | Scalaire | Quadrivecteur |
| L'échelle | Résolution de la distance | Résolution angulaire | Résolution temporelle | Résolution spatio-temporelle |
| L'espace | Le temps | L'espace-temps-djinn | |||
|---|---|---|---|---|---|
| Distance | Angle | Espace-temps | Djinn | ||
| La grandeur primaire | Position | Orientation | Instant | Temps propre | Djinn propre |
| La grandeur conservative associée | Impulsion | Moment angulaire | Énergie | Impulsion Énergie Moment angulaire | Impulsion d'échelle Énergie d'échelle Moment angulaire d'échelle |
| Les types de variables | Vecteur | Vecteur | Scalaire | Vecteur à cinq composantes10 | |
6. Quelques applications en géographie
La théorie des fractales doit être au cœur de l'explication géographique. Cependant, sa mise en œuvre en géographie présente deux difficultés :
(1) la définition de Laurent Nottale est une sorte de synthèse de nombreux concepts mathématiques qu'il faut connaître ;
(2) cette définition demeure malgré tout trop simpliste pour les problèmes géographiques car dès que l'on essaye de les théoriser, on se heurte à leur complexité. En physique, ce n'est pas le cas puisque l'on peut toujours partir du cas le plus simple pour aller vers les cas les plus complexes. En revanche, en géographie, le simple n'existe pas. Il faut s'attaquer, presque sans filet, directement au complexe.
Toutefois, difficile ne signifie pas impossible. Une multitude d'essais existe, et fait encore école. La suite de ce mémoire essaye de présenter quelques applications possibles en géographie, parfois, en faisant quelques détours, mais toujours avec l'objectif ultime d'établir une théorie des discontinuités en géographie par des équations parfaitement continues expliquant la morphogenèse d'objet géographique.
6.1. Retour à Boves : vers un modèle spatio-temporel
Depuis 2005, deux événements sont venus compléter les études de l'espace géographique picard du Xe au XXIe siècle : un texte dans le Géopoint 2006 (Forriez, Martin, 2006, à paraître) et une amorce d'étude beaucoup plus complexe lors de mon stage avec Laurent Nottale (juin-juillet 2006). Aussi, il faut en présenter une synthèse de ce qui a été fait d'une part, de ce qu'il reste à faire d'autre part.
6.1.1. La méthode pour mener l'étude spatio-temporelle
Pour mener à bien l'étude spatio-temporelle, une fiche a été construite pour recueillir les données relatives à l'espace géographique et à la chronologie historique de chaque motte et/ou château. Cette fiche sert de support dans la construction d'un système d'information géographique sur MapInfo 6. La première carte (Forriez, 2005) comportait de nombreuses lacunes. La plus importante était de ne pas pouvoir ajouter facilement la « découverte » d'un nouveau site. Pour y remédier, toutes les communes de l'espace historique picard (Pas-de-Calais, Somme, une partie de l'Oise et une partie de l'Aisne) ainsi que de nombreux « lieux-dits » (ancien village rattaché à une commune-centre), ont été reporté sur une nouvelle carte. Il est à noter que la carte support reste celle de 2005 (60 km autour d'Amiens).
FICHE N°
| Nom de la commune : | Lieu-dit : | Code postal : | |||||||||||||||||||
| |||||||||||||||||||||
| État antérieur : □ villa à proximité □ autre : |
| |||||||||||||||||||
Historique (rapide bilan des grandes phases connues du site castral) :
| |||||||||||||||||||||
| Schéma spatial du site castral : | Schéma chronologique du site castral :
| ||||||||||||||||||||
| Dépendant de : | Statut : □ domaine royal : □ bailliage □ sénéchaussée □ prévôté □ intendance □ autre | |||||||||||||||||||
carte 1 = 60 km autour d'Amiens carte 2 = cartes de Roger AGACHE | Statut : □ seigneurie □ baronnie □ vicomté □ comté □ marquisat □ duché □ principauté | ||||||||||||||||||||
| Zone historique : □ carte du XIe siècle reconstitué □ carte de l'Amiénois au XIIIe siècle □ carte de la Picardie bourguignonne au XVe siècle | Enregistrer sur PC : □ oui □ non | ||||||||||||||||||||
Le recueil des données relatives à l'étude spatio-temporelle des mottes et/ou châteaux de l'espace picard historique est très difficile. En effet, il n'existe aucun ouvrage de synthèse répertoriant la totalité des mottes et châteaux. De plus, les bases de données disponibles au service régional d'archéologie de Picardie sont fortement incomplètes. Richard Jonvel (2006) l'a montré. Aussi, pour mener une étude globale, la principale source de données sera provisoirement la base de données des 36 000 communes de France du Quid (http://www.quid.fr). Cela permet déjà de savoir où se localise principalement les mottes et châteaux. Un nettoyage de cette première base sera donc nécessaire pour une étude plus exhaustive. Aussi, une fiche est systématiquement ouverte pour chaque commune. Actuellement, seul l'Amiénois a été dépouillé de manière systématique ce qui représente un peu plus de 500 communes, l'ensemble de l'espace en regroupant à peu près 3 000.
De plus, la localisation des sites castraux reste imprécise. Nombreux sont les textes qui mentionnent un château dans telle ou telle commune dont nous ne savons rien de sa localisation. Aussi, pour prendre en compte ce problème, les cercles matérialisant le château ou la motte ont un diamètre de 1 kilomètre. Reste ainsi le problème de la taille des grandes agglomérations comme Amiens qui ont pu accueillir plusieurs châteaux en leur sein.
Bien qu'imprécise, la figure 28 montre une cohérence dans la répartition des châteaux et des mottes : on les trouve à proximité des grands axes de communication (voies romaines, cours d'eau) ou dans des zones stratégies comme au niveau de la « frontière » entre l'Amiénois et le Ponthieu (Forriez, 2005). Cette nouvelle carte, beaucoup plus complète que la précédente (Forriez, 2005 ; Forriez, Martin, 2006), permet tout de même de remarquer que la répartition atemporelle des mottes et châteaux de l'Amiénois reste hétérogène malgré tout.
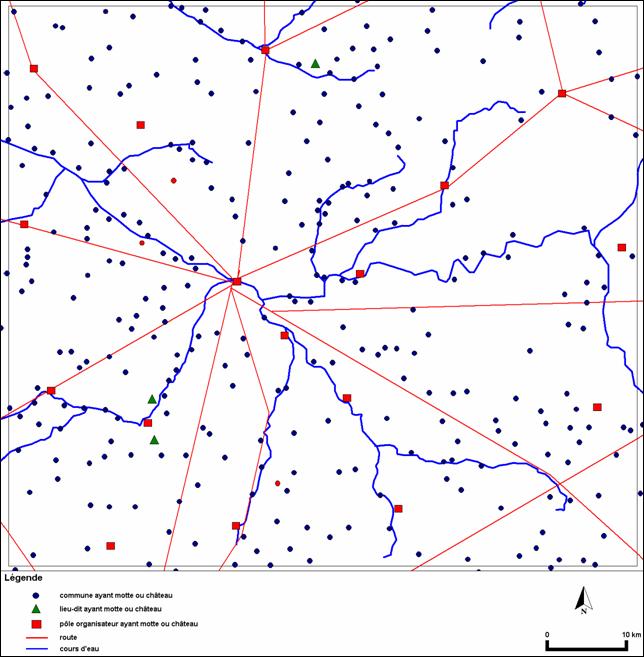
6.1.2. La réflexion sur l'analyse spatio-temporelle
6.1.2.1. Le temps
6.1.2.1.1. La loi de l'évolution de Laurent Nottale (2000)
Les données historiques et/ou archéologiques sont incertaines. La connaissance de la date de construction, ou de destruction, d'une motte, ou d'un château, peut varier de l'année près au siècle près. Il est donc plus simple de cartographier le nuage des mottes et châteaux que d'établir la répartition temporelle. Pour y remédier, nous allons modéliser ce temps historique par l'intermédiaire de la loi de l'évolution de Laurent Nottale (et alii, 2000), à savoir :
![]() où
où ![]()
avec k entier si le nombre d'embranchements (choix potentiels à chaque bifurcation du système) reste constant à chaque étape et si D est un exposant qui relie le rapport d'échelle au nombre d'embranchements, et T0 l'origine de l'évolution considérée déterminée par un événement arbitrairement choisi à n = 0.
Il s'agit d'une loi phénoménologique puisqu'elle est restreinte à des phénomènes particuliers. Avant d'appliquer l'équation, il faut caler les données avec trois dates. Ce calage consiste à calculer g et TC à partir des premières dates. Il faut préciser que
![]() et
et ![]()
Autrement dit, la série chronologique est déterminée par l'origine spatio-temporelle que l'on a choisie. On calcule ensuite g et TC entre n et n + 1 de la manière suivante :
![]()
![]()
Ce type d'équation n'est pas exceptionnel en soi. Elle porte le nom de convergence géométrique se formulant de la manière suivante :
![]()
Ce point présente la particularité d'être super stable.
Dans la pratique, il faut ajuster numériquement g et TC par une méthode d'estimation statistique comme celle des moindres carrés. On peut utiliser aussi comme estimateur statistique la variable t de Student dans un tirage de Monte-Carlo (fig. 30).
6.1.2.1.2. L'archétype de Boves
Aujourd'hui, l'exemple de Boves sert toujours d'archétype. Le site archéologique de Boves se situe à huit kilomètres au sud-est d'Amiens. Il est essentiellement d'époque médiévale et il fait l'objet d'une étude très approfondie depuis dix ans (Racinet, 1996-2006). C'est un complexe castral constitué d'une motte (élévation de terre vraisemblablement ou partiellement anthropique), d'un château et de bâtiments d'habitation et/ou ecclésiastiques (Racinet et Drouin, 2002 ; Racinet, 2004).
C'est bien sûr grâce à tous les travaux existant sur ce site que cette étude a pu être possible et réalisée. Ainsi, dix « dates remarquables » ont été retenues pour construire le modèle. Les quatre premières ont été choisies en fonction des données archéologiques. 920 et 960 correspondent aux deux premières structures en bois construites sur la motte. Vers 1025 les occupants ont mis en place une structure mi-pierre, mi-bois. Vers 1140, ils commencent à bâtir le premier château à proprement parler. Par l'étude d'Olivier Leblanc (2003), nous savons que la motte est ensuite occupée de manière continue. Le château connaît alors plusieurs transformations et reconstructions.
| n | Date réelle | g(n, n + 1, n + 2) | k | TC(0, n) | TC(n, n + 1, n + 2) | log(Tn ‐ TC) |
| BIFURCATION | ||||||
| 0 | 920 | 1,32 | ||||
| 1 | 960 | 0,62 | 3 | 856,00 | 856,00 | 1,78 |
| 2 | 1025 | 0,57 | 3 | 870,71 | 875,50 | 2,10 |
| 3 | 1140 | 0,52 | 4 | 883,34 | 899,05 | 2,38 |
| 4 | 1360 | 0,90 | 1 | 62,47 | –876,67 | 2,66 |
| BIFURCATION | ||||||
| 5 | 1604 | 0,72 | 2 | 762,08 | 746,23 | 2,85 |
| 6 | 1945 | 3,02 | ||||
| BIFURCATION ? | ||||||
Les six dernières dates sont obtenues à partir de sources historiques déjà exploitées. Entre 1360 et 1380, les ducs de Lorraine reconstruisent le château. Vers 1604, ce dernier château est détruit, ce qui débouche sur une occupation de moins en moins intensive. Du XIXe au XXIe siècle, le site est réactivé en 1870, lors de la guerre franco-allemande puis en 1914-1918, lors de la première guerre mondiale et enfin en 1939-1945, lors de la seconde guerre mondiale. À partir de 1997 débutent les fouilles archéologiques. Une simplification a été réalisée afin de résumer les quatre dernières dates entre la fin du XIXe siècle et le XXe siècle en une seule. En effet, leur connaissance précise n'est due qu'à la proximité temporelle que nous avons par rapport à elles. Aussi, ces quatre dates ont été « résumées » par la date 1945 qui est symbolique de la fin des guerres franco-allemandes et du début de la construction européenne. De plus, la dernière trace « en dur » (un bloc de béton armé) laissée sur le chantier date de cette époque.
La figure 29 donne une première estimation de g et une estimation du nombre k d'embranchements possibles avec : ![]() , et deux estimations de TC. Elle montre une décélération (Cash et alii, texte pdf).
, et deux estimations de TC. Elle montre une décélération (Cash et alii, texte pdf).
Après plusieurs tests manuels, on trouve une valeur g comprise entre 0,56 (de n0 à n4) et 0,68 (de n5 à n6). La différence des valeurs s'explique sans doute par la présence d'une bifurcation entre n4 et n5 (fig. 29). Laurent Nottale a confirmé ces résultats en effectuant un tirage de type Monte Carlo afin d'ajuster g et TC en utilisant l'estimateur statistique de la variable t de Student (fig. 30). On constate que pour g ≈ 0,56938 on observe un pic de la variable t de Student avec un TC ≈ 870 pour les cinq premières dates de la série. Il n'y a qu'une chance sur 50 000 d'obtenir ces résultats au hasard.
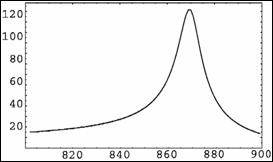
La valeur de TC est donc voisine de 870. Cette valeur n'est pas aberrante ni pour l'historien ni pour le géographe, puisqu'il s'agit du moment où l'empire carolingien se désagrège.
La fonction de bifurcation f(X) (fig. 31) varie comme la fonction ![]() où m est le nombre de bifurcations. Le problème est que dans le cas de Boves m n'est pas constant, d'où la nécessité de diviser la courbe en au moins deux parties : dans la première, m = 3, dans la seconde m = 2. La rupture de pente de la courbe peut être interprétée, aussi comme une bifurcation.
où m est le nombre de bifurcations. Le problème est que dans le cas de Boves m n'est pas constant, d'où la nécessité de diviser la courbe en au moins deux parties : dans la première, m = 3, dans la seconde m = 2. La rupture de pente de la courbe peut être interprétée, aussi comme une bifurcation.
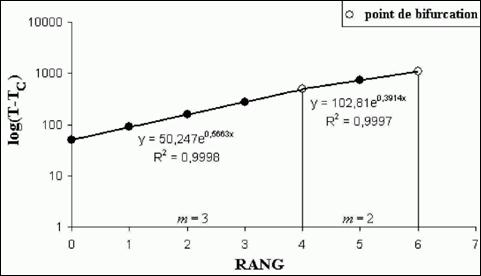
La figure 32 présente les dates théoriques obtenues à partir des valeurs de g et de TC choisies, réinjectées dans l'équation de l'évolution.
| n | Date théorique | g optimisé | log(Tn – TC) | k |
| BIFURCATION | ||||
| 0 | 920 | 1,70 | ||
| 1 | 959 | 0,56 | 1,95 | 3 |
| 2 | 1028 | 0,56 | 2,20 | 3 |
| 3 | 1150 | 0,56 | 2,45 | 3 |
| 4 | 1366 | 0,56 | 2,70 | 3 |
| BIFURCATION | ||||
| 5 | 1600 | 0,68 | 2,86 | 2 |
| 6 | 1944 | 0,68 | 3,03 | 2 |
| BIFURCATION ? | ||||
On constate ainsi qu'après chaque bifurcation supposée, le nombre d'embranchements, c'est-à-dire en fait l'ampleur du choix, diminue. Il passe de trois à deux. Puis, si on prend comme date suivante 2080 (Nottale et alii, 2000), il passe de deux à un. Ce qui, en soi, pour une occupation d'un site archéologique, c'est-à-dire un site qui a subi une « extinction », est très logique.
De plus, d'un point de vue purement mathématique, on remarque que :
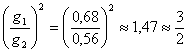
ce qui correspond bien à l'hypothèse des trois embranchements qui sont portés au nombre de deux après la bifurcation temporelle.
La figure 33 montre le nombre de choix d'évolutions possibles. Au début, il y a une rupture entre l'empire carolingien et le système féodal, marquée par une désagrégation spatiale. De 920 à 1360, il y a, à chaque « moment historique » trois branches possibles donc trois futurs potentiels dont seulement un se réalisera. Cela étant, le système ne semble avoir réellement bifurqué qu'à partir du moment où le nombre de choix possibles s'est réduit à deux (en 1360). La bifurcation peut s'expliquer par l'intégration définitive, à une échelle plus petite, du site de Boves dans l'Etat français en construction.
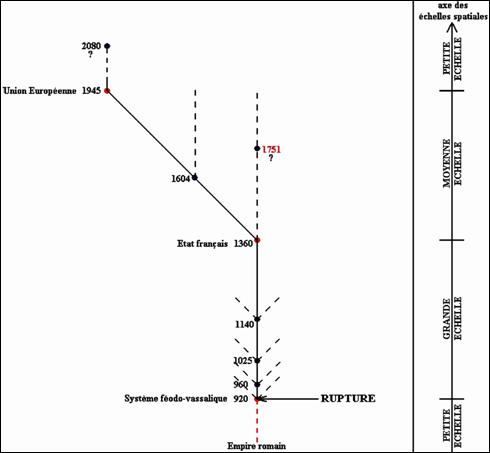
Si l'évolution s'était poursuivie autrement (absence d'Etat français par exemple), l'étape suivante de construction aurait eu lieu, sur la motte, vers 1751 (?). Quelle forme cette césure aurait-elle pu prendre ? Quelle nouvelle structure territoriale aurait pu, là, prendre naissance ? Nous ne le savons pas mais certains scénarii pourraient être échafaudés.
Rappelons qu'après 1748, année du traité d'Aix la Chapelle, et la constitution de la Prusse et de l'Autriche « la possibilité d'une hégémonie française sur l'Europe disparaît » (Duby, 1971, t.3, p. 246). La France devra ensuite ferrailler d'abord pendant la Révolution, puis entre 1869 et 70, puis entre 1914 et 1918 puis enfin entre 1939 et 1945 pour assurer son existence.
La seconde bifurcation a lieu en 1945, si on prend comme TC = 2080, et si on considère comme recevables les résultats de Laurent Nottale et alii (2000). Là, il n'y a plus qu'un choix possible. L'évolution du site n'a plus qu'une possibilité, qu'une branche. Tout comme les états antérieurs, cela peut s'expliquer par l'intégration européenne. Il ne présente plus aucun intérêt quels que soient les niveaux considérés, sauf au niveau scientifique. À partir de là, il n'est pas impossible de penser que le site de Boves restera dans son état actuel : c'est-à-dire à l'abandon jusqu'à la prochaine rupture (2080 ?) qui peut être lui redonnera un intérêt stratégique.
6.1.2.1.3. Bilan et perspective
Enfin, il faut préciser que, pour l'ensemble des séries temporelles, trois cas sont possibles (lorsqu'il existe au moins trois dates connues) : (1) l'accélération ; (2) la décélération ; (3) l'oscillation non amortie. À la vue des données déjà recueillies, les trois possibilités semblent exister. Il faudra en dresser une moyenne pour constater si, globalement, la tendance est une accélération, une décélération ou une oscillation non amortie.
6.1.2.2. L'espace
Cela étant, l'approche de Laurent Nottale demeure avant tout temporelle. Aussi, faut-il la compléter par une analyse spatiale, notamment à partir de l'équation de Schrödinger généralisée (Nottale, 1993 ; Nottale et alii, 2000, p. 350-353). Nous l'esquisserons ci-dessous. Cette approche permettra d'essayer de comprendre l'organisation de la distribution dans l'espace des châteaux (fig. 28). Cette étude n'a pas pour but d'être exhaustive. Elle vise seulement à dégager des pistes de recherche fondées sur une analyse spatiale et fractale.
6.1.2.2.1. L'analyse spatiale
La méthode est assez simple (Martin, 1997 ; 2003b). On calcule une succession de densités de châteaux en fonction de la surface de cercles tracés autour d'un pôle organisateur c'est-à-dire des principaux châteaux. On reporte ensuite les valeurs sur un graphique avec en abscisse le logarithme la taille du rayon (de cinq kilomètres en cinq kilomètres) et en ordonnée le logarithme du rapport : ![]() .
.
Le calcul est appliqué autour de dix positions, supposées être des pôles organisateurs au Xe siècle : Boves, Amiens, Corbie, Vignacourt, Picquigny, Moreuil, Poix, Conty, Folleville et Albert (ou Ancre au Moyen Age) (Forriez, 2005). Il est donc postulé un lien de subordination qui s'exprimerait par une hiérarchie spatiale. Afin de mener à bien cette réflexion, il faut partir d'un postulat partiellement vrai. Celui-ci consiste à supposer que le nombre des châteaux recensés dans le comté d'Amiens primitif n'a pas varié au cours du temps. Cela implique que la distribution se serait cristallisée entre le Xe et le XIIIe siècle, ce qui est historiquement très discutable.
Après une étude approfondie de l'organisation de l'espace autour de chaque château, on observe deux types de structures spatiales : celui rencontré à Boves, Amiens, Corbie, Albert et Moreuil qui correspond à un polynôme qui « croît puis décroît », et celui trouvé à Picquigny, Poix, Vignacourt et Conty qui se résume à un polynôme qui seulement « décroît ». Une seule structure paraît inclassable : c'est celle de Folleville.
Cela étant, dans ce classement, il faut prendre en compte les effets de bord. Les structures du premier type couvrent presque toute la totalité du comté d'Amiens primitif avec des cercles dont le rayon varie entre 15 et 20 km ; celles du second voire du troisième type intègrent un effet de bordure presque immédiat au-delà de 5 km.
En prenant le nombre moyen de châteaux, on obtient un modèle plus « général », qui exprime une « sur densification » moyenne entre 5 et 25 km, puis une décroissance entre 25 et 75 km de l'effectif des châteaux. Cela étant, cette variation moyenne masque une décroissance exponentielle au-delà de 25 km (fig. 34).
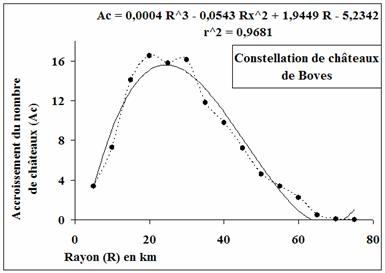
Ainsi, une fois normée avec la surface, la décroissance devient parfaitement exponentielle. L'ajustement est parfait au-delà de 15 km. En conséquence la distribution spatiale de la constellation des châteaux n'est pas fractale au sens de Benoît Mandelbrot (invariance d'échelle). Pour avoir une structure fractale, il aurait fallu que la densité décroisse en fonction des échelles, ce qui est bien le cas ici, mais aussi qu'elle décroisse d'une même valeur entre les échelles, ce qui n'est pas le cas ici. La distribution moyenne est ici exponentielle ce qui correspond à une « super-fractale » selon la classification de Laurent Nottale (1993).
Toutefois, l'analyse spatiale n'est pas complète. Il aurait fallu pour cela automatiser les calculs sur les mottes et/ou châteaux et intégrer l'évolution territoriale et la distribution spatiale des sites castraux du comté primitif d'Amiens à la France actuelle. Cependant, ces premiers résultats sont suffisants pour envisager de sérieuses pistes de recherches. En effet, à partir de la nouvelle carte (fig. 28), une nouvelle analyse spatiale a pu être réalisée sous Mathematica 4, par Laurent Nottale, lors de mon stage au C.N.R.S. à l'Observatoire de Meudon. Le programme reprend l'analyse réalisée en 2005 et essaye de mener une étude systématique en tout point (c'est-à-dire en toute commune) de la corrélation entre la distance (jouant le rôle d'un rang) et la densité de mottes et châteaux observée (fig. 35). D'après Laurent Nottale, les fonctions polynomiales observées (Forriez, 2005, p. 128-141) correspondrait à des polynômes de Laguerre qui servent dans l'étude des fonctions radiales en mécanique quantique. Autrement dit, s'il s'agit effectivement de telles fonctions, ce serait un indice de l'état quasi-quantique de l'espace géographique.
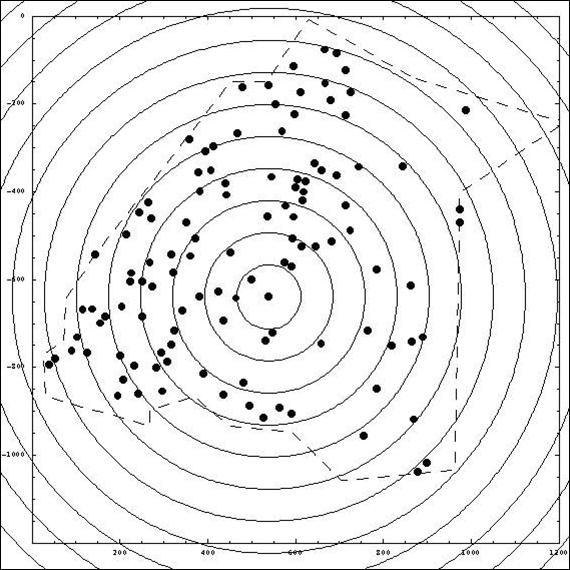
Les polynômes de Laguerre sont des solutions d'une équation différentielle linéaire du second ordre sans second membre : ![]() . Ce sont des polynômes orthogonaux de degré n ayant pour produit scalaire
. Ce sont des polynômes orthogonaux de degré n ayant pour produit scalaire ![]() . En mécanique quantique, ils donnent la dépendance radiale des fonctions d'onde de l'atome hydrogène. Les polynômes de Laguerre permettent de calculer la divergence exponentielle d'une fonction radiale R(x). On appelle fonction radiale R(x), une fonction
. En mécanique quantique, ils donnent la dépendance radiale des fonctions d'onde de l'atome hydrogène. Les polynômes de Laguerre permettent de calculer la divergence exponentielle d'une fonction radiale R(x). On appelle fonction radiale R(x), une fonction ![]() où x est la variable radiale. Il s'agit d'une fonction d'onde particulière. Les polynômes de Laguerre sont des fonctions particulières des fonctions de Laplace.
où x est la variable radiale. Il s'agit d'une fonction d'onde particulière. Les polynômes de Laguerre sont des fonctions particulières des fonctions de Laplace.
Soit an, coefficient de xn : ![]() avec
avec ![]() . Les polynômes de Laguerre Ln(x) vérifient l'équation différentielle :
. Les polynômes de Laguerre Ln(x) vérifient l'équation différentielle : ![]() . Ils vérifient également les récurrences suivantes :
. Ils vérifient également les récurrences suivantes :
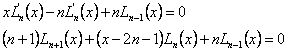
Le calcul des coefficients des polynômes de Laguerre s'effectue de la manière suivante :

Pour conclure, les polynômes de Laguerre sont obtenus par le développement en série de la fonction génératrice suivante : 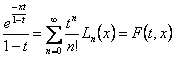 . Les polynômes de Laguerre ont pour norme pour le produit scalaire :
. Les polynômes de Laguerre ont pour norme pour le produit scalaire : ![]() . Les premiers polynômes de Laguerre sont :
. Les premiers polynômes de Laguerre sont :

Les polynômes de Laguerre associés sont les polynômes de Laguerre tels que :
![]() .
.
6.1.2.2.2. L'analyse fractale
L'analyse spatiale radiale aboutit à l'établissement d'une dimension fractale locale, c'est-à-dire la dimension en chaque lieu servant de centre. Malheureusement, une simple moyenne ne peut établir la « vraie » dimension fractale qui correspondrait à la dimension globale du nuage de points. Aussi, il faudrait calculer une des dimensions fractales générales. La dimension de boîtes semble la plus approprier. Le programme de calcul est en cours de construction sur Mathematica 4.
6.1.2.2.3. Bilan et prospectives
Du fait, du manque d'information temporelle, l'analyse spatiale est très limitée. Il faut se contenter pour le moment d'effectuer les analyses dans l'état actuel des connaissances (XXIe siècle). Toutefois, la connaissance de données temporelles plus fiables permettra de réaliser des sortes « d'arrêt sur image » en précisant la date de la carte des châteaux, d'en faire l'analyse spatiale.
6.1.2.3. L'espace-temps
On pourra ainsi dégager une dynamique temporelle, mais également d'échelle. À partir de là, la (re)connaissance d'un état spatial initial permettrait de développer des scenarii sur l'état final (actuel) de modéliser les différentes bifurcations spatiale et temporelle de l'espace historique picard des mottes et châteaux. Comment peut-on faire une telle analyse .
6.1.2.3.1. Le rôle de l'équation de Schrödinger généralisée
La combinaison de l'analyse temporelle et spatiale aboutira à la définition d'un état initial auquel on pourra appliquer l'équation de Schrödinger généralisée. Elle permet d'organiser une diffusion auto organisée dans les échelles, qui ressemble très grossièrement à une diffusion spatiale dans les temps. Ensuite, il suffira de comparer les résultats théoriques avec les résultats du système d'information géographique pour paramétrer le modèle, c'est-à-dire la recherche des constantes. Ainsi, la fonction d'onde ψ correspondra ici à la probabilité de trouver un château à une distance d pour un temps t, mais aussi à la probabilité de trouver un château à une distance d pour une échelle ε.
De plus, une modélisation de l'espace géographique par l'équation de Schrödinger généralisée semblerait plus efficace que les automates cellulaires ou les systèmes multi-agents dans les modèles de dynamique et de simulation spatiale. L'élaboration de la procédure et du programme reste un grand chantier à réaliser.
6.1.2.3.2. Bilan et prospective
Pour conclure, on peut dire que grâce à une certaine forme de stabilité des données spatiales et temporelles, l'étude temporelle menée sur Boves et l'analyse spatiale menée sur l'espace historique picard pourra servir de modèle dans l'étude d'autres espaces plus récents, notamment dans l'objectif d'une prospective de tel ou tel aménagement à court, moyen et long terme. L'espace-temps de Laurent Nottale, appliqué en sciences humaines, suppose donc une réorientation de la géographie et de l'histoire, c'est-à-dire une réconciliation structurelle entre une vision spatiale (géographique) et temporelle (historique). Ainsi, on est contraint d'abandonner définitivement la vision braudélienne du géographe plantant le décor et de l'historien expliquant le rôle des acteurs.
6.2. Population des villes mondiales : du modèle linéaire aux modèles non linéaires
Cette étude a été menée dans le cadre d'un article dans le cadre des rencontres ThéoQuant 2007 (Forriez, Martin, 2007, à paraître). Elle clarifie la loi rang-population urbaine, bien connue en géographie depuis un siècle, et propose (enfin) une solution pour introduire l'espace géographique dans cette loi en proposant un modèle beaucoup plus élaboré et complexe que le modèle classique linéaire, développé depuis Georges Kingsley Zipf.
6.2.1. Présentation de la loi rang-taille
Le modèle de Pareto (1896) est rarement employé sous sa forme classique en géographie. En effet, il a été présenté autrement par Georges Kingsley Zipf (1932 ; 1935 ; 1941 ; 1949), qui a été le premier à étudier systématiquement les distributions de tailles des mots par rapport à leur rang par ordre décroissant en l'appelant « loi rang-taille ». Walter Christaller (1933 ; Lösch, 1940) a repris ce type de modèle pour expliquer la distribution spatiale du réseau urbain de sa théorie des lieux centraux : la population Pi d'une ville i en fonction de son rang ri dans son ensemble de villes nationales ou régionales ordonnées par tailles décroissantes obéit à la loi suivante :
![]()
q est un exposant voisin de 1 et K correspond à la taille de la plus grande ville (P0 = K). Lorsque le paramètre q prend la valeur 1, la signification de la loi rang-taille est particulièrement simple : elle décrit la population des villes comme une progression géométrique inverse de leur nombre (ou de leur rang).
Georges Kingsley Zipf analysait les distributions observées en référence à la droite qui les ajuste sur un graphique bi logarithmique, avec la population en ordonnées et le rang en abscisses :
ln Pi = ln K – ln ri.
Cependant, cette expression est strictement équivalente à celle du modèle de Pareto, puisque le rang ri d'une ville i est exactement la même chose que le nombre de ville N(Pi) dont la population est supérieure ou égale à un certain seuil Pi. Dans le modèle de Pareto, l'exposant est appliqué à la taille et non au rang :
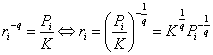 .
.
Ensuite, il suffit de poser : ![]() pour obtenir la loi Zipf-Mandelbrot (Pumain, Saint-Julien, 1997 ; Pumain, 2006) :
pour obtenir la loi Zipf-Mandelbrot (Pumain, Saint-Julien, 1997 ; Pumain, 2006) :
![]() .
.
Si q est une dimension fractale, il ne faut jamais oublier que tous les exposants trouvés correspondront à l'inverse de la dimension fractale.
6.2.2. Relativité d'échelle et loi rang-taille
A la lumière de la relativité d'échelle, on peut clarifier cette approche empirique. La loi rang-taille montre que si l'on reporte, plus généralement, une variable V, par exemple la population urbaine en fonction du logarithme de l'inverse du rang rn, la distribution s'ajuste à une loi de puissance de la forme :
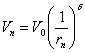
où δ est identifié à la dimension fractale D. Cette équation devient la solution d'une équation différentielle d'échelle du premier ordre de la forme :
![]() .
.
La solution de cette équation est de la forme :
![]()
qui est la forme classique de l'invariance d'échelle. On peut par conséquent rapprocher cette équation de l'équation 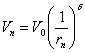 . Il suffit de poser :
. Il suffit de poser :
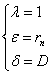
λ correspond à la constante d'intégration qui sera identifiée à ce que l'on appelle l'échelle de coupure c'est-à-dire à la résolution à partir de laquelle un phénomène devient fractal ou, au contraire, non fractal. Dans le cas des lois rang-taille, elle sera égale à 1. Cependant, le simple fait d'avoir identifier λ = 1 nous autorise à prendre n'importe quelle valeur pour λ. En effet, le fait de modifier cette constante n'aura pour conséquence que de translater la courbe vers la gauche ou vers la droite. ε est une résolution. δ correspond à la dimension fractale et V0 à la valeur initiale de la série.
Nous allons maintenant présenter la relation classique entre le rang et la population urbaine, classée en ordre décroissant qui est l'exemple classique des lois rang-taille en géographie. On la trace généralement sur un graphique bi logarithmique. Par commodité mathématique, nous utiliserons le logarithme népérien. Cet espace bi logarithmique sera appelé espace des échelles. L'équation ![]() (fig. 36) devient :
(fig. 36) devient :
![]() .
.
Autrement dit, il s'agit bien sur un graphique bi logarithmique d'une droite dans laquelle la pente correspond à la dimension fractale D (fig. 37). Il faut remarquer que la dimension fractale correspond, elle, à la dérivée de ln V par rapport au ln ε :
![]() .
.
Nous proposons, pour tester cette loi, d'étudier la base de données de l'ONU qui recense les 435 premières villes ou conurbations mondiales disponible sur le web (http://www.populationdata.net/palmaresvilles.php).
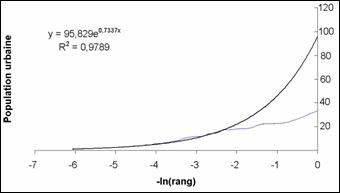
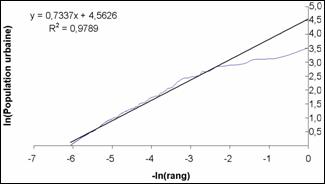
On constate que l'ajustement statistique n'est pas satisfaisant. D'ailleurs, il est probable qu'aucune série ne correspond parfaitement à une loi puissance pure. En effet, sur la figure 37, on voit très bien qu'à partir de la valeur –2, l'ajustement diverge complètement par rapport aux données analysées. Pour y remédier, il suffit d'ajuster un polynôme du second degré dans l'espace des échelles (Laherrère, 1996, Pumain, 2006) (fig. 38).
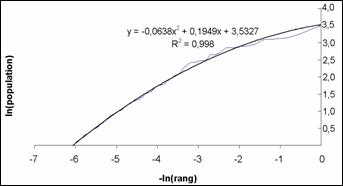
Est-ce une curiosité ? Une anomalie ? Est-ce la preuve que l'approche fractale est inadaptée pour une étude géographique ? Vraisemblablement pas ! En étendant le concept d'invariance d'échelle à celui de dépendance d'échelle, il est possible de faire fond sur la géométrie fractale pour mieux décrire cette structure d'ordre qui transparaît dans le réseau urbain mondial sommairement rendu par le niveau des populations des agglomérations.
6.2.3. Loi rang-taille parabolique
Nous avons pu ajuster dans l'espace des échelles une parabole (fig. 38), ce qui correspond à une équation de la forme :
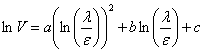
ce qui se transforme en :
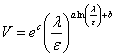 .
.
c = V0 et on appellera la constante ec = C, ce qui donne une loi de Gibrat généralisée.
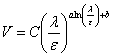 .
.
En effet, pour obtenir la loi de Gibrat classique (1931 ; Armatte, 1995), il suffit de poser, en redéfinissant les constantes :
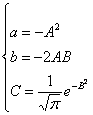
Dans l'équation de Gibrat généralisée, nous constatons que l'exposant est devenu variable. En effet, si on reprend, en vertu du principe de covariance, la définition de la dimension fractale, à savoir la dérivée de ln V par rapport à ln ε, on obtient donc :
![]()
2aln ε + b qui correspond à la définition de la dimension fractale de Laurent Nottale est devenue variable.
On notera en outre que 2aln ε + b correspondrait grosso modo à la variable z = aln(x – x0) + b de la loi de Gibrat.
De plus, une limite particulière doit retenir notre attention :
![]()
Autrement dit, lorsque ε tend vers 1, la dimension fractale devient constante et correspond à un cas d'invariance d'échelle. On peut alors poser :
b = D0.
Nous allons maintenant essayer de trouver l'origine de la loi parabolique. Nous savons :
![]()
or ici D = D(ln ε) = 2aln ε + b. Nous introduisons cette donnée dans l'équation précédente ce qui nous donne :
![]()
ce qui s'intègre très facilement en séparant les variables.

![]()
Ce résultat, illustré par la figure 39, est remarquable à plus d'un titre. Il permet de résoudre un problème posé par Jean Laherrère dans son Compte rendu à l'Académie des Sciences (1996), mais aussi de définir un attracteur qui montre une stabilité exceptionnelle dans l'espace des échelles, de la structure observée sur la figure 40.
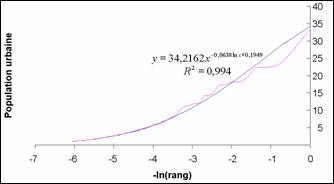
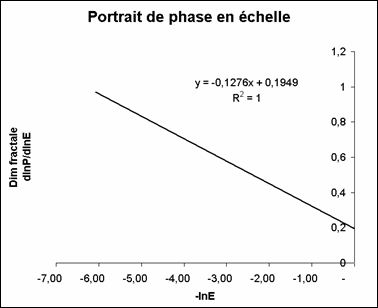
Cependant, l'interprétation reste délicate. En effet, comme toutes les lois d'échelle, l'équation différentielle d'échelle parabolique est dans sa forme absolue. Autrement dit, les populations urbaines peuvent croître, la forme de la relation restera inchangée. Il est donc logique que l'ajustement parabolique soit toujours plus proche de la structure analysée. Toutefois on peut obtenir un meilleur ajustement avec un modèle non linéaire intégrant une correction log-périodique de la loi de puissance.
6.2.4. Correction log-périodique et loi rang-taille
Nous nous sommes longtemps questionnés face à nos données pour savoir si la meilleure solution était une correction log-périodique invariante d'échelle ou dépendante d'échelle.
Le plus simple a été de les tester toutes les deux. À l'issue des calculs, il s'est avéré que nous avions à faire à une dépendance d'échelle log-périodique. Contrairement à la théorie, nous n'allons pas ajouter une valeur critique car, ici, ce n'est pas nécessaire puisque l'inverse du rang ordonné de façon décroissante tend vers zéro. Nous allons donc multiplier l'équation 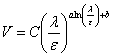 par une correction log-périodique, ce qui donne :
par une correction log-périodique, ce qui donne :
![]()
dans notre cas, β = 0,1 et ω = 4, en première approximation.
Dans ce cas, la dimension fractale sera égale à :
![]() .
.
Il faut remarquer que la partie réelle est une fonction. Il n'y a donc aucune raison d'interdire la mise en fonction de la partie imaginaire de D' ce qui permettrait d'obtenir un meilleur ajustement. En plus, c'est peut-être par la partie imaginaire que l'on pourrait introduire l'espace géographique dans les lois rang-taille. Elle correspond peut-être à la dimension fractale du nuage de points des villes étudiées. Les données n'étant pas à notre disposition pour vérifier cette hypothèse, la question reste ouverte.
Comme les lois de puissance, cette correction log-périodique demeure profondément analytique. Il faut essayer maintenant d'identifier les variables la paramétrant. À quoi correspondent β et ω ? Cela reste à établir. Autrement dit, sans relation annexe, il est extrêmement difficile de paramétrer la courbe. Pourtant, de nombreux phénomènes en géographie présentent clairement, de manière intuitive, des oscillations log-périodiques, mais il est extrêmement difficile de les paramétrer. Toutefois, la figure 41 montre bien qu'un ajustement log-périodique est beaucoup plus pertinent pour la loi rang vs population urbaine, même si le coefficient de détermination est un peu plus faible.
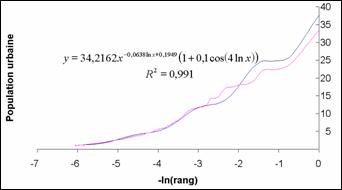
Les figures 42 à 44 montrent évidemment un attracteur cyclique présentant deux régimes : un premier régime qui englobe le second et concerne les premiers villes mondiales d'un point de vue de la population. Le second régime présente le cas général des petites et moyennes villes.
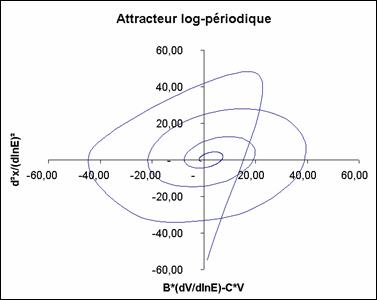
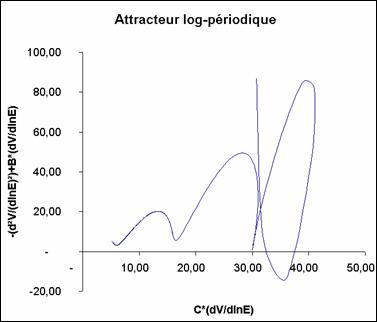
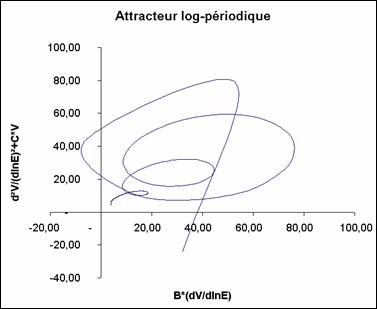
6.2.5. Quelques notes sur l'indice G de Philippe Martin
L'indice G a été utilisé par Philippe Martin (2004b) pour l'étude des reliefs dont l'analyse fractale montrait des polynômes dans l'espace des échelles :
![]()
où DA est une « dimension fractale asymptotique » et a est le coefficient en x2 du polynôme du second degré (fig. 45).
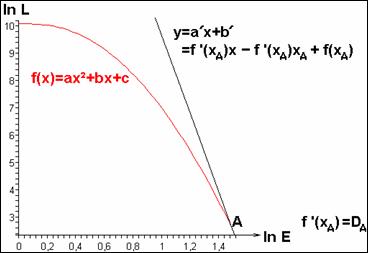
Aujourd'hui, on peut démontrer cet indice de manière suivante. Lorsque x → xA, on peut écrire :
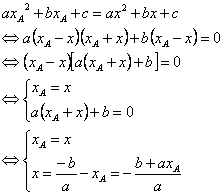
or, on sait que la dimension fractale DA correspond au nombre dérivé de la tangente en xA. Il suffit donc d'écrire :
![]() .
.
L'indice G correspond donc mathématiquement à :
![]() lorsque x → xA.
lorsque x → xA.
G traduit alors, de manière synthétique, la dépendance d'échelle et permet d'écrire une équation non linéaire
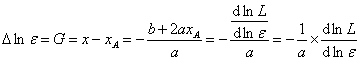
or on sait, par définition, que
![]()
donc
![]()
c'est-à-dire l'équation non linéaire
![]() .
.
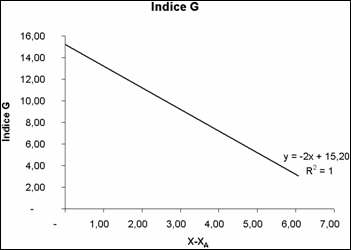
Après l'exemple de la loi rang-taille où xA = ln(435) (fig. 46), un deuxième projet de recherche se dessine alors en reprenant les travaux de Philippe Martin (2004b). On sait grâce à eux qu'il existe une relation entre l'indice G et l'altitude h qui a été avérée empiriquement. L'explication mathématique de G ouvre la possibilité de fonder une théorie de la morphogenèse du relief, presque exclusivement perçue comme une structuration issue d'une dynamique d'échelle ! En effet, G correspondrait selon toute vraisemblance à une force d'échelle constante. Autrement dit, l'évolution d'un relief quelconque (le temps) deviendrait mineure dans le processus d'émergence d'un relief. Une théorie purement spatiale pourra ainsi être formulée.
6.3. Le modèle du R.I.K.S. Un exemple de processus fractal appliqué à un automate cellulaire modélisant l'espace géographique
Nombreux sont les modèles de simulation où les fluctuations fractales sont négligées. Parmi eux, on peut citer le modèle du R.I.K.S (Research Institute for Knowledge Systems). J'ai découvert ce modèle d'automate cellulaire lors de mon stage à Besançon (novembre 2006). Il est très intéressant car la fonction de transition à micro échelle une fonction puissance correspondant à un cas de dépendance d'échelle. Or, les principaux concepteurs du modèle (White, Engelen, 1993, 1997 ; Engelen, White, Uljee, 1997 ; White, 1998) ont découvert cette formule de manière empirique. L'objectif de cette partie est de reprendre dans un cadre plus théorique les résultats de l'article.
6.3.1. Description des paramètres du modèle à micro échelle
C'est un modèle à trois paramètres : (1) la suitability ; (2) l'accessibilité ; (3) l'effet de voisinage.
La suitability est un nombre attribué à chaque cellule j en fonction de l'intérêt à apporter à ce lien. Elle est notée Zj.
L'accessibilité de la cellule j au réseau de transport est notée Tj.
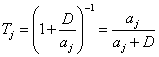
D est la distance entre la cellule j et la cellule la plus proche à travers laquelle j est connectée au réseau. aj est un coefficient représentant l'importance de l'accessibilité du réseau pour l'aménagement de j. Il exprime le fait que pour de nombreuses activités telles que l'industrie, un accès direct au système routier est plus important que pour d'autres comme l'agriculture.
L'effet de voisinage Cj est calculé de la manière suivante.
![]()
ω est le poids du paramètre appliqué à l'aménagement de k à la position x dans une distance d de son voisinage. r est une fonction de Dirac où r = 1 si la cellule est occupée par l'aménagement k et sinon r = 0. Cj est donc une constante dépendante de d et de x.
La transition se réalise avec une perturbation stochastique. Un potentiel Qj pour chaque fonction (vecteur de transition des potentiels) est calculé pour chaque cellule telle que :
![]()
où
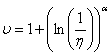 avec η est une variable stochastique et
avec η est une variable stochastique et ![]() , sinon le modèle n'est pas réaliste.
, sinon le modèle n'est pas réaliste.
On peut rapprocher la fluctuation stochastique de la fonction de transition à une loi dépendance d'échelle.
6.3.2. Etude de la fluctuation stochastique
L'articulation micro-macro est au cœur de cette fluctuation stochastique. Comment la réintroduire, comment la contrôler ? Les lois d'échelle sont l'unique outil que les mathématiques nous offrent. Autrement dit, cela revient à un problème fractal, qui est résolu par le calcul du potentiel Qj qui sert à faire la transition entre les états de chaque cellule. Reprenons :
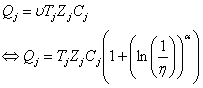
TjZjCj est une constante obtenue par un paramétrage avec la suitability, l'accessibilité et l'effet de voisinage. Nous allons le contracter en :
![]() .
.
6.3.2.1. Variable stochastique fractale
On obtient donc
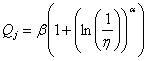
ce qui correspond presque à la loi d'échelle standard (Nottale, 1993) :
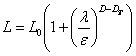
où L correspond à une longueur, L0 à la longueur initiale, DT est la dimension topologique, D est la dimension fractale, λ est l'échelle de coupure et ε est la résolution.

Essayons de redéfinir le terme 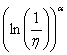 comme étant égal à
comme étant égal à ![]() c'est-à-dire :
c'est-à-dire :
 .
.
Cependant, on constate alors que :
![]() .
.
Dès lors, le but des calculs suivants sera de tenter de rétablir cette égalité.
6.3.2.1.1. Hypothèse de départ
η est une variable stochastique que nous allons identifier à un mouvement brownien en première approche. Sa dimension fractale est donc égale à 2. De plus, on sait que ![]() .
.
Recherchons une formule unissant α, D et DT. On trouve, après quelques essais, que : ![]() ce qui limite l'étude de la variation de la dimension topologique, soient trois cas DT = 0, DT = 1 et DT = 2.
ce qui limite l'étude de la variation de la dimension topologique, soient trois cas DT = 0, DT = 1 et DT = 2.
6.3.2.1.1.1. DT = D = 2
![]()
![]() . Soit la borne maximale pour laquelle la simulation demeure réaliste.
. Soit la borne maximale pour laquelle la simulation demeure réaliste.
6.3.2.1.1.2. DT = 1 et D = 2
![]()
![]() , ce qui correspond à un cas intermédiaire.
, ce qui correspond à un cas intermédiaire.
6.3.2.1.1.3. DT = 0 et D = 2
![]()
![]() . Soit la borne minimale pour laquelle la simulation demeure réaliste.
. Soit la borne minimale pour laquelle la simulation demeure réaliste.
6.3.2.1.1.4. Conclusion partielle et prospective
Résumonsles cas étudiés :
(1) si DT < 0 alors ![]() . Le modèle est impossible à modéliser.
. Le modèle est impossible à modéliser.
(2) si DT > 2 alors ![]() . Le modèle est impossible à modéliser car nous rentrons dans le domaine à trois dimensions.
. Le modèle est impossible à modéliser car nous rentrons dans le domaine à trois dimensions.
Il faudra bien sûr dans la perspective d'une approche complète reprendre ces résultats pour en réaliser le cas général.
6.3.2.1.2. Démonstration de la fractalité par la construction de l'indice γ
Reprenons : ![]() , on va supposer qu'il existe un nombre fractionnaire γ tel que
, on va supposer qu'il existe un nombre fractionnaire γ tel que ![]() . On trouve :
. On trouve :
![]() .
.
On peut donc écrire :

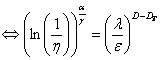
Il nous faut d'abord vérifier que l'indice empirique γ fonctionne.
| DT = D = 2 | DT = 1 et D = 2 | DT = 0 et D = 2 | |
| D – DT = | 0 | 1 | 2 |
| indéfini | 2 | ||
| 0 |
Ce tableau montre que l'indice γ est indéfini quand DT = D = 2, ce qui nous fait restreindre notre étude à (DT = 1 et D = 2) et (DT = 0 et D = 2).
Ensuite, rappelons que nous cherchions une équivalence entre 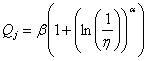 et
et 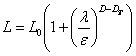 . Pour cela, on pose :
. Pour cela, on pose : ![]() et
et ![]() et
et ![]() , ce qui donne :
, ce qui donne :
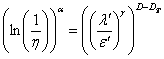
mais comme ![]() , on peut écrire que :
, on peut écrire que :
![]()
![]() c'est-à-dire
c'est-à-dire ![]() .
.
Grâce à cette formule, on comprend pourquoi la formule de Robert White et de George Engelen ne fonctionnait qu'avec le logarithme d'une variable stochastique. En effet, par définition, ![]() donc
donc
![]() ;
;
![]() car le logarithme népérien est une fonction croissante dans IR et on sait qu'il existe une asymptote verticale en 0 ;
car le logarithme népérien est une fonction croissante dans IR et on sait qu'il existe une asymptote verticale en 0 ;
![]() ;
;
or ![]() < 0 donc
< 0 donc ![]() > 0.
> 0.
![]() permet donc de contrôler la fractalité urbaine dans le sens où l'expression doit vraisemblablement contenir l'échelle de coupure λ' et la résolution ε'. Malheureusement, les calculs précédents n'ont pas réussi à trouver une formule exprimant λ' et ε' de manière indépendante de – ln η. Cependant, pourquoi a-t-on besoin d'un terme aléatoire ? Tout simplement parce que nous ne pouvons pas mesurer de manière précise comment telle ou telle cellule va se déployer dans l'ordre des échelles. En effet, le modèle prend également en compte des facteurs humains, difficilement modélisable, d'où la nécessité de faire appel à une variable stochastique permettant d'envisager le maximum de possibilités.
permet donc de contrôler la fractalité urbaine dans le sens où l'expression doit vraisemblablement contenir l'échelle de coupure λ' et la résolution ε'. Malheureusement, les calculs précédents n'ont pas réussi à trouver une formule exprimant λ' et ε' de manière indépendante de – ln η. Cependant, pourquoi a-t-on besoin d'un terme aléatoire ? Tout simplement parce que nous ne pouvons pas mesurer de manière précise comment telle ou telle cellule va se déployer dans l'ordre des échelles. En effet, le modèle prend également en compte des facteurs humains, difficilement modélisable, d'où la nécessité de faire appel à une variable stochastique permettant d'envisager le maximum de possibilités.
Enfin, il faudrait revenir sur notre hypothèse de départ (le mouvement brownien) et faire varier la dimension fractale entre 0 et 2.
6.3.2.2. Signification mathématique et intérêt du terme aléatoire
Toute l'étude précédente montre que le terme aléatoire de la fonction de transition de Robert White et George Engelen permet effectivement de contrôler la propagation entre l'échelle micro et l'échelle macro. C'est lui qui permet de placer les échelles de coupure λ entre le domaine fractal et le domaine non fractal (fig. 47). Autrement dit, c'est lui qui contrôle la fractalité de chaque cellule et qui permet de parfaitement contrôler l'automate cellulaire. Nous avons ainsi redécouvert empiriquement la notion de « chaos interne » défini par Laurent Nottale (1993), c'est-à-dire, formulé de manière très raccourcie, qu'il est certain que le modèle est incertain.
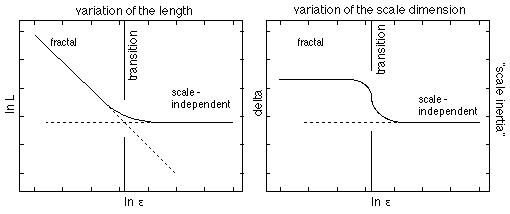
Le premier graphique montre qu'un objet peut être fractal à micro échelle et non fractal à macro échelle. La transition est matérialisée par λ. Le deuxième graphique montre que la dimension fractale reste constante à une échelle micro et disparaît après l'échelle de transition λ pour revenir à la dimension topologique.
6.3.3. Conclusion
Le modèle du R.I.K.S. présente bien une dépendance d'échelle dont l'étude semble avoir été négligée au profit d'une certaine fonctionnalité du modèle. Toutefois, observations et analyse fractale montrent qu'elles ne sont pas contradictoires.
7. Conclusion générale. Géographie et relativité d'échelle, vers une géographie mathématique
Faire un bilan est toujours quelque chose de très délicat lorsque l'on sait que les conclusions apportées seront provisoires. Elle s'articulera en deux points. D'abord, un récapitulatif de la géographie, de la relativité d'échelle et de l'espace géographique quasi quantique est nécessaire. Ensuite, la description du projet de ma thèse en reprenant quelques conseils d'André Dauphiné semble être une bonne ouverture.
7.1. Géographie et relativité d'échelle
Ce mémoire s'est acharné à montrer que géographie et relativité d'échelle possédaient de nombreux points communs. Leur rapprochement implique entre autres à construire ce que l'on a appelé espace géographique quasi quantique. Toutefois, ils ont tout de même des points de divergences forts car la relativité d'échelle est une théorie issue de la physique. Aussi, avant de construire l'espace géographique quasi quantique, il faudra bien comprendre la signification géométrique et analytique des variables physiques pour ne pas tomber dans ce que l'on pourrait appeler de la physique géographique. Ainsi, il faudra construire une véritable « géographie mathématique » comme le montre la définition de l'indice G. Le modèle spatio-temporel reste largement à construire. L'avantage de l'étude de l'espace picard historique est que l'on dispose d'un temps long dans lequel on peut dégager des règles générales que l'on pourrait appliquer à d'autres cas géographiques. Afin, une première clarification des lois rang-population urbaine et de son rapport à l'espace a pu être avancée grâce à la théorie de la relativité d'échelle. Qu'est-ce que la géographie mathématique .
7.2. Projet d'une géographie mathématique
Pour Emmanuel Kant, « la géographie physique est […] un abrégé universel de la nature ; et comme elle ne constitue pas seulement le fondement de l'histoire mais aussi celui de toutes les géographies possibles, il faudrait traiter brièvement des parties principales de chacune d'entre elles » (Kant, éd. 1999, p. 73). Il distinguait ainsi cinq géographies principales : la géographie mathématique, la géographie morale (diversité des mœurs), la géographie politique (fondée grâce à la géographie physique), la géographie de marché (localisation du commerce et de la production) et la géographie théologique (répartition des religions). Ces différents domaines de la géographie sont bien sûr plus ou moins dépassés et révélateurs d'une certaine idéologie.
La géographie mathématique d'Emmanuel Kant renvoie à la cartographie, à la description du mouvement de la terre dans le système solaire et aux notions de physiques classiques. Aujourd'hui, cette géographie mathématique a évolué vers les études morphologiques (structures). Mon projet consiste à laisser la cartographie comme elle est, à laisser la description du mouvement de la terre aux astrophysiciens, mais à introduire l'espace de la mécanique quantique en géographie, en remarquant qu'Emmanuel Kant ne pouvait pas connaître un tel espace. Ainsi, mon espace de travail est un espace quasi quantique. Pour ne pas alourdir davantage le texte avec les théories de la mécanique quantique, j'ai choisi de les exposer dans ma future thèse. De plus, je pense que la présentation de la théorie des fractales était déjà assez imposante d'un point de vue mathématique.
Toutefois, André Dauphiné (1978) rappelle trois dangers des mathématiques : (1) le désir de faire du modernisme ; (2) les erreurs d'interprétation ; (3) les simplifications abusives. Aussi, toute la difficulté de la définition d'un espace géographique fractal telle qu'elle a été formulée dans ce mémoire, est bien de louvoyer entre ces trois écueils possibles. En revanche, André Dauphiné (1978) précise également qu'une démarche quantitative et de conceptualisation permettra : (1) préciser un concept existant ; (2) enrichir les concepts existants ; (3) formuler de nouveaux concepts. C'est évident dans cet objectif qu'il faudra poursuivre les recherches.
8. Bibliographie
La bibliographie ne se contente pas de mentionner les ouvrages cités (en gras), mais quelques ouvrages qui ont contribué à la rédaction de ce mémoire de master 2.
60 km autour d'Amiens. Echelle 1:170 000, Montreuil, Cartes – Plans – Guides Blay Foldex, 2004.
AGACHE, Roger, BREART, Bruno, 1975, Atlas d'archéologie aérienne de Picardie. Le bassin de la Somme et ses abords à l'époque protohistorique et romaine, 2 tomes, Amiens, Société des Antiquaires de Picardie, 164 p.
ARMATTE Michel, 1995, « Robert Gibrat et la loi de l'effet proportionnel », in Mathématiques et sciences humaines, n°129, p.5-35.
ARON, Raymond, 1969, La philosophie critique de l'histoire. Essai sur une théorie allemande de l'histoire, Paris, Le Seuil, 320 p. [Points E18]
AYRES, Frank, 1972, Théorie et applications des équations différentielles, trad. fr. Paris, Série Schaum, 296 p.
AYRES,, Franck, SCHMIDT, Philip A., 1978, Les mathématiques de base, trad. fr., Paris, 422 p. [Série Schaum]
BABELON, Jean-Pierre, 1989, Château de France au siècle de la Renaissance, Paris, Flammarion, 840 p.
BACHELARD, Gaston, 1934, Le nouvel esprit scientifique, Paris, PUF, 184 p. [Quadrige]
BACHELET, Bernard, 1999, L'espace, Paris, PUF, 128 p. [Que sais-je ? 3383]
BACRY, Henri, 2000, La symétrie dans tous les états, Paris, Vuibert, 448 p.
BAILLY, Antoine, BEGUIN, Hubert, 1982, Introduction à la géographie humaine, Paris, Armand Colin, 216 p.
BAILLY, Antoine, FERRAS, Robert, PUMAIN, Denise (s.d.), 1995, Encyclopédie de géographie, Paris, Economica, 1168 p.
BAK, Per, 1999, Quand la nature s'organise. Avalanches, tremblements de terre et autres cataclysmes, trad. Marcel FILOCHE, Paris, Flammarion, 284 p.
BASS, Jean, 1964, Cours de mathématiques, t. 1, Matrices et tenseurs – Courbes et surfaces. Intégrales simples et multiples. Séries et intégrales de Fourier. Fonctions orthogonales. Fonctions eulériennes, Paris, Masson, XXXII-1016 p.
BASS, Jean, 1964, Cours de mathématiques, t. 2, Fonctions analytiques. Equations différentielles et aux dérivées partielles. Calcul symbolique – Fonctions harmoniques. Calcul des variations – Abaques – Algèbre de Boole, Paris, Masson, XXXII-1016 p.
BASS, Jean, 1971, Cours de mathématiques, 3 tomes, Paris, Masson, 1968, XXXIV-1226 p., 406 p. [4e édition]
BASS, Jean, 1974, Eléments de calcul des probabilités, Paris, Masson, XII-276 p.
BAUD, Pascal, BOURGEAT, Serge, BRAS, Catherine, 2003, Dictionnaire de géographie, Paris, Hatier, 544 p. [Initial]
BAUDELLE, Guy, REGNAULD, Hervé, 2004, Echelles et temporalités en géographie, Paris, Sedes, 174 p. [Dossiers des Images Economiques du Monde]
BAYLON, Christian, MIGNOT, Xavier, 1999, La communication, Paris, Nathan, 416 p. [Fac linguistique]
BEGUIN, Hubert, 1979, Méthodes d'analyse géographique quantitative, Paris, Litec, 252 p.
BEGUIN, Hubert, THISSE, Jean, 1979, « An axiomatic approach to geographical space », in Géographical analysis, n°11, p. 325-341.
BENKIRANE, Réda, 2002, La Complexité, vertiges et promesses. 18 histoires de sciences, Paris, Le Pommier, 420 p.
BERGE, Pierre, POMEAU, Yves, DUBOIS-GANGE, Monique, 1994, Des rythmes au chaos, Paris, Odile Jacob, 294 p.
BERGE, Pierre, POMEAU, Yves, VIDAL, Christian, 1988, L'ordre dans le chaos. Vers une approche déterministe de la turbulence, Paris, Hermann, 352 p.
BERGE, Pierre, POMEAU, Yves, VIDAL, Christian, 1998, L'espace chaotique, Paris, Hermann, 162 p.
BERNARD-WEIL, Elie, 1988, Précis de systémique ago-antagoniste, L'interdisciplinaire éditeur, 230 p. [Limoneste]
BOURBAKI, Nicolas, 1970, Eléments de mathématique. Théorie des ensembles, Paris, Hermann.
BOURBAKI, Nicolas, 1970, Eléments de mathématique. Algèbre. Chapitres 1 à 3, Paris, Hermann.
BOURBAKI, Nicolas, 1967, Eléments de mathématique. Algèbre. Chapitres 4 et 5, Paris, Hermann, 222 p.
BOURBAKI, Nicolas, 1964, Eléments de mathématique. Algèbre. Chapitres 6 et 7, Paris, Hermann, 174 p.
BOURBAKI, Nicolas, 1954, Eléments de mathématique. Algèbre. Chapitre 8, Paris, Hermann, 190 p.
BOURBAKI, Nicolas, 1959, Eléments de mathématique. Algèbre. Chapitre 9, Paris, Hermann, 212 p.
BOURBAKI, Nicolas, 1971, Eléments de mathématique. Topologie générale. Chapitres 1 à 4, Paris, Hermann.
BOURBAKI, Nicolas, 1974, Eléments de mathématique. Topologie générale. Chapitres 5 à 10, Paris, Hermann.
BOURBAKI, Nicolas, 1961, Eléments de mathématique. Fonctions d'une variable réelle (Théorie élémentaire), Paris, Hermann, 200 p.
BOUTOT, Alain, 1993, L'invention des formes, Paris, Odile Jacob, 376 p.
BRUNET, Roger, 1980, « La composition des modèles dans l'analyse spatiale », L'espace géographique, n°4, p. 253-265
BRUNET, Roger, 1987, La carte, mode d'emploi, Paris, Fayard, 270 p.
BRUNET, Roger, 1990, Mondes nouveaux. Le déchiffrement du monde, volume 1, livre 1, Paris, Hachette, 552 p. [Géographie universelle]
BRUNET, Roger, 2001, Le déchiffrement du monde. Théorie et pratique de la géographie, Paris, Belin, 402 p.
BRUNET, Roger, FERRAS, Robert, THERY, Hervé, 1992, Les mots de la géographie. Dictionnaire critique, Paris, Reclus, p. 518. [Collection Dynamiques de territoire]
CALVO, Adina, CALVO, Bernard, 1996, Algèbre générale, Paris, Masson, 192 p. [Amphi sciences]
CARTAN, Henri, 1967, Calcul différentiel, Paris, Hermann, 178 p. [Collection Méthodes]
Carte topographique d'Amiens, 1993, Paris, IGN. [Orange n°2308]
CASH, Roland, CHALINE, Jean, NOTTALE, Laurent, GROU, Pierre, « Développement humain et loi log-périodique », http://wwwusr.obspm.fr/~nottale/arcash.pdf
CHAITIN, Gregory, 2006, « Les limites de la raison mathématique », Pour la science, n°342, avril p. 70-76.
CHALINE Jean, MARCHAND, Didier, 2002, Les merveilles de l'évolution. Editions universitaires de Dijon, Dijon, 268 p.
CHALINE, Jean, NOTTALE, Laurent, GROU, Pierre, 1999, « L'arbre de la vie a-t-il une structure fractale ? Le point sur… », Comptes rendus de l'Académie des sciences, n°329, série II, p.849-851.
CHAZAL, Gérard, 1997, Formes, figures, réalités, Seyssel, Champ Vallon, 248 p.
CHOSSAT, Pascal, 1996, Les symétries brisées, Paris, Pour la science, 112 p.
CHOUQUER, Gérard, 2000, L'étude des paysages. Essais sur leurs formes et leur histoire, Paris, Rasse, 208 p.
CHRIST, Yvan, 1978 Dictionnaire des châteaux de France, t. 4, THIEBAUT, Jacques, Artois, Flandre, Hainaut, Picardie. Nord, Pas-de-Calais, Somme, Aisne, Paris, Berger-Levrault, 328 p.
CHRISTALLER, Walter, 1933, Die zentralen orte in Süddeutschland : eine ökonomisch-geographische untersuchung über die gesetz massigkeit der verbreitung und entwicklung der siedlungen mit städtischen funktionen, Jean, Fischer Verlag.
CLAVAL, Paul, 2003, Causalité et géographie, Paris, L'Harmattan, 126 p.
COHEN-TANNOUDJI, Claude, DIU, Bernard, LALDE, Franck, 1977, Mécanique quantique, 2 tomes, Paris, Hermann, XVI-1518 p.
DAMERON, Jean-Claude, 1994, Analyse mathématique schématisée, t. 1, Les bases, Paris, Economica, XII-374 p.
DAMERON, Jean-Claude, 1995, Analyse mathématique schématisée, t. 2, Les fonctions, Paris, Economica, XII-330 p.
DAMERON, Jean-Claude, 1997, Analyse mathématique schématisée, t. 3, Les développements, Paris, Economica, XII-270 p.
DAMERON, Jean-Claude, 1997, Analyse mathématique schématisée, t. 4, L'intégration, Paris, Economica, XIV-358 p.
DARDEL, Eric, 1990, L'homme et la terre, Paris, CTHS, 200 p.
DARNIERE, Luck, « Qu'est-ce que la théorie des modèles ? », http://math.univ-angers.fr/~darniere/ThMod.html
DAUPHINE, André, 1978, « Mathématiques et concepts en géographie », in Géopoint 1978, Avignon, p. 7-53
DAUPHINE, André, 1987, Les modèles de simulation en géographie, Paris, Economica, 188 p.
DAUPHINE, André, 1995, Chaos, fractales et dynamiques en géographie, Paris, Reclus, 136 p.
DAUPHINE, André, 2003, Les théories de la complexité chez les géographes, Paris, Economica, 248 p. [Anthropos]
DAUPHINE, André, 2006, « Emergence et multifractalité des formes. Un exemple d'application en géographie urbaine », in Colloque Géopoint 2004 : La forme en géographie, Avignon, Groupe Dupont et UMR ESPACE 6012 du CNRS éditeurs, p.281-286.
DELAHAYE, Jean-Paul, 1999, Information, complexité et hasard, Paris, Hermès, 276 p.
Département de la Somme. Carte routière et administrative. Echelle 1:125 000, 1999, Paris, carte IGN.
DESCARTES, René, 1999 [réédition], Le discours de la méthode pour bien conduire sa raison, et chercher la vérité dans les sciences, Paris, Librio, 94 p.
DESMARAIS, Gaëtan, 1998, Les cahiers de géographie du Québec, « Trois concepts-clés pour les modèles morphodynamiques de la ville », vol. 42, n°117, p. 399-449.
DESMARAIS, Gaëtan, RITCHOT, Gilles, 2000, La géographie structurale, Paris, L'Harmattan, 148 p.
DUBOIS, Jacques, 1995, La dynamique non linéaire en physique du globe, Paris, Masson, XIV-266 p.
DUBOIS, Jacques, CHALINE, Jean, 2006, Le monde des fractales. La géométrie cachée de la nature, Paris, Ellipses, 312 p.
DUBY Georges (s.d.), 1971, Histoire de la France. t. 1 : Des origines à 1348, 414 p. ; t. 2, De 1348 à 1852, 455 p. ; t. 3, De 1852 à nos jours, 448 p. Editions Larousse, Paris.
DUMOLARD, Pierre, DUBUS, Nathalie, CHARLEUX, Laure, 2003, Les statistiques en géographie, Paris, Belin, 240 p. [Atout géographie]
DURAND, Daniel, 2002, La systémique, Paris, p.U.F., 128 p. [Que sais-je ? 1795]
EINSTEIN, Albert, 1956, La relativité, trad. Maurice Solovine, Paris, Payot, 220 p. [Petite bibliothèque Payot]
EINSTEIN, Albert, 1990, Conceptions scientifiques, trad. Maurice SOLOVINE et Daniel FARGUE, Paris, Flammarion, 188 p. [Champs 214]
ENGELEN, Georges, WHITE, Robert, ULJEE, I., 1997, « Integrating constrained cellular automata models, GIS and decisions support tools for urban planning and policy making », in Decision support systems in urban planning, London, Edition Harry p.J. Timmermans, p. 125-155.
FLORY, Georges, 1974, Formulaire de mathématiques spéciales. Algèbre. Analyse. Géométrie. Cinématique, Paris, Vuilbert, 170 p.
FORRIEZ, Maxime, 2005, La motte de Boves permet-elle de mener une réflexion épistémologique commune en archéologie, en géographie et en histoire ?, Arras, Mémoire de master 1 d'histoire et de géographie, 156 p.
FORRIEZ, Maxime, 2005, « Structure spatiale et archéologie. Exemple des M.N.T. », in RACINET, Philippe, Recherches pluridisciplinaires sur un terroir picard de l'époque antique à la Révolution français. Boves, complexe castral et prioral du « Quartier Notre-Dame ». Document final de synthèse. Campagnes 2003-2005, Amiens, SRA Picardie et Laboratoire d'histoire et d'archéologie de l'Université de Picardie, p. 115-131.
FORRIEZ, Maxime, MARTIN, Philippe, 2006, « De l'utilité de la théorie de la relativité d'échelle de Laurent Nottale. Partie 1. Recherche d'un modèle scalaire spatio-temporel », in Géopoint 2006, Avignon, Groupe Dupont et UMR Espace 6012 du CNRS éditeurs, 6 p. [en cours de publication]
FORRIEZ, Maxime, MARTIN, Philippe, 2006, « De l'utilité de la théorie de la relativité d'échelle de Laurent Nottale. Partie 2. Application d'un modèle scalaire spatio-temporel », in Géopoint 2006, Avignon, Groupe Dupont et UMR Espace 6012 du CNRS éditeurs, 9 p. [en cours de publication]
FORRIEZ, Maxime, MARTIN, Philippe, 2007, « Structures hiérarchiques en géographie : des modèles linéaires aux modèles non linéaires (lois de puissance et corrections log-périodiques) » in TheoQuant 2007, Besançon, 14 p. [en cours de publication]
FOSSIER, Robert, 1968, La terre et les hommes en Picardie, 2 tomes, Paris, Béatrice-Nauwelaerts, 824 p.
FOSSIER, Robert, 1974, Histoire de la Picardie, Toulouse, Privat, 458 p.
FRANKHAUSER, Pierre, 1994, La fractalité des structures urbaines. Anthropos économica édition, Paris, 291 p.
FRANKHAUSER, Pierre, PUMAIN, Denise, 2001, « Fractales et géographies », in Lena SANDERS, Modèles en analyse spatiale, Paris, Lavoisier, 334 p.
FREMONT, Armand, 1976, La région, espace vécu, Paris, PUF, 288 p.
GANTMACHER, Félix R., 1966, Théorie des matrices, trad. Ch. SARTHOU, 2 tomes, Paris, Dunod, XIV-370 p., XII- 268 p.
GAUTHIER, Yvon, La mesure du chaos, http://mapageweb.umontreal.ca/lepagef/dept/cahiers/Gauthier_mesure_du_chaos.pdf, 30 p.
GAUTHIER, Yvon, 1997, Logique et fondements des mathématiques, Paris, Diderot Multimédia, II, 174 p.
GIBRAT, Robert, 1931, Les inégalités économiques, Paris, Sirey.
GIRAUD, Gaël, 2000, La théorie des jeux, Paris, Flammarion, 318 p.
GLEICK, James, 1991, La théorie du chaos. Vers une nouvelle science, trad. Christian JEANMOUGIN, Paris, Flammarion, 431 p.
GOULD, Stephen Jay, 2005, Le renard et le hérisson. Comment combler le fossé entre la science et les humanités, trad. Nicolas WITKOWSKI, Paris, Le Seuil, 266 p. [Science ouverte].
GOUYET, Jean-François, 1992, Physique et structures fractales, Paris, Masson, XIV-234 p.
GRATALOUP, Christian, 1996, Lieux d'histoire. Essai de géohistoire systématique, Paris, Reclus, 200 p. [Espace modes d'emploi]
GRAWITZ, Madeleine, 2001, Méthodes des sciences sociales, Paris, Dalloz, XIV-1020 p.
GRIBBIN, John, 1994, Le chat de Schrödinger. Physique quantique et réalité, trad. Christel ROLLINAT, Paris, Flammarion, 330 p. [Champs 312]
GUERMOND, Yves, 2005, Modélisations en géographie. Déterminismes et complexités, Paris, Lavoisier, 388 p.
GUERIN-PACE, France, 1993, Deux siècles de croissance urbaine. La population des villes françaises de 1831 à 1990, Anthropos, Paris, 205 p. [Villes]
GUERRIEN, Bernard, 1995, La théorie des jeux, Paris, Economica, 108 p. [Economie poche]
GUININ, Daniel, AUBONNET, François, JOPPIN, Bernard, 1996, Précis de mathématiques. Algèbre 1, Paris, Bréal, 264 p.
HAGGETT, Peter, 1973, L'analyse spatiale en géographie humaine, trad. fr., Paris, Armand Colin, 390 p. [U]
HAWKING, Stephen, 1989, Une brève histoire du temps. Du big bang aux trous noirs, trad. Isabelle NADDEO-SOURIAU, Paris, 246 p. [Champs 238]
HEGEL, Georg Wilhelm Friedrich, 1965 [réédition], La raison dans l'histoire, trad. Kostas PAPAIOANNOU, Paris, Plon, 312 p.
HEMPEL, Carl, 1996, Eléments d'épistémologie, trad. Bertrand SAINT-SERNIN, Paris, Armand Colin, VIII-184 p. [Cursus]
HLADIK, Jean, 1993, Le calcul tensoriel en physique, Paris, Masson, XVI-172 p.
http://wwwusr.obspm.fr/~nottale/
http://www.quid.fr/
JONVEL, Richard, 2006, Les mottes castrales dans l'arrondissement d'Amiens. Topographie et géographie des fortifications médiévales, Mémoire de Master 1 sous la direction de Philippe Racinet, Université de Picardie Jules Verne, Amiens, 148 p.
KANT, Emmanuel, 1999, Géographie, trad. Michèle COHEN-HALIMI, Max MARCUZZI et Valérie SEROUSSI, Paris, Aubier, 394 p.
KLEIN, Etienne, 1995, Le temps : un exposé pour comprendre, un essai pour réfléchir, Paris, Flammarion, 125 p. [Dominos]
KLEIN, Etienne, 2004, Les tactiques de chronos, Paris, Flammarion, 220 p.
KRIVINE, Jean-Louis, 1988, Théorie des ensembles, Paris, Cassini, 274 p.
KUHN, Thomas, 1983, La structure des révolutions scientifiques, trad. Laure MEYER, Paris, Flammarion, 286 p. [Champs 115]
KUNZMANN, Peter, BURKARD, Franz-Peter, WIEDMANN, Franz, 1993, Atlas de la philosophie, trad. Zoé HOUSEZ et Stéphane ROBILLARD, Paris, Le livre de Poche, 278 p. [La pochothèque]
« L'infini, le fini, le discret et le continu », Tangente. L'aventure mathématique, Paris, Pole, Hors-série 13, 2006, 156 p.
« La complexité. La science du XXIe siècle », Pour la science, Paris, Pour la science SARL, 314, 2003, 176 p.
« La magie des fractales », Tangente. L'aventure mathématique, Paris, Pole, Hors-série 18, 2004, 52 p.
LAHERRERE, Jean, 1996, « Distributions de type " fractal parabolique " dans la nature », in Comptes rendus de l'Académie des Sciences, t.322, série IIa, p. 535-541.
LAM NINA, Siu-Ngan, COLA de, Lee, 1993, Fractal in geography, PTR Prentice-Hall, Englewood Cliffs, New Jersey, 308 p.
LANDAU, Lev Davidvitch, LIFCHITZ, Evgueni, 1989, Physique théorique, t. 2, Théorie des champs, trad. Sergueï MEDVEDEV, Moscou, Mir, 520 p.
« Les fractales. Art, nature et modélisation », Bibliothèque Tangente. L'aventure mathématique, Paris, Pole, Hors série 18, 2004, 156 p.
LE MEHAUTE, Alain, 1990, Les géométries fractales. L'espace-temps brisé, Paris, Hermès, 198 p.
LE MEHAUTE, Alain, NIGMATULLIN, Raoul R., NIVANEN, Laurent, 1998, Flèches du temps et géométrie fractale, Paris, Hermès, 348 p.
LE MOIGNE, Jean-Louis, 1977, La théorie du système général. Théorie de la modélisation, Paris, PUF, 338 p.
LEBLANC, Olivier, 2003, Les seigneurs de Boves. Origines et exercices du pouvoir en Picardie (IXe-XIIIe siècle), Amiens, Thèse de l'université de Picardie.
LEDUC, Jean, 1999, Les historiens et le temps : conceptions, problématiques, écritures, Paris, Le Seuil, 328 p. [Points H259]
LEVY, Jacques, LUSSAULT, Michel, 2003, Dictionnaire de la géographie et de l'espace des sociétés, Paris, Belin, 1034 p.
LOSCH, Albert, 1940, Die räumliche ordnung der wirtschaft, Iena, Fischer.
LURCAT, François, 1999, Le chaos, Paris, PUF, 128 p. [Que sais-je ?]
LUYCKX GHISI, Marc, 2001, Au-delà de la modernité, du patriarcat et du capitalisme. La société réenchantée ?, Paris, L'Harmattan, 216 p.
MABY, Jean (s.d.), 2003, Objets et indicateurs géographiques, Avignon, Université d'Avignon, 316 p. [Collection Actes Avignon n°5]
MALEK, J., Chaos déterministe : le concept et son histoire, http://homepages.ulb.ac.be/~jmalek/chap1.pdf, p. 1-9.
MALEK, J. Les principaux concepts et résultats de la théorie du chaos déterministe, http://homepages.ulb.ac.be/~jmalek/chap2.pdf, p. 10-31.
MANDELBROT, Benoît, 1967, « How long is the coast of Britain ? Statistical self – similarity and fractional dimension », in Classics on fractals, edited by G. E. EDGAR, 1993, Addison – Wesley publishing company, Reading, Massachusetts, USA, p.351-358.
MANDELBROT, Benoît, 1975, Les objets fractals, Paris, Flammarion, 208 p.
MANDELBROT, Benoît, 1997, Fractales, hasard et finances (1959-1997), Paris, Flammarion, 246 p.
MANNEVILLE, Paul, 1991, Structures dissipatives chaos et turbulence, Paris, Commissariat à l'énergie atomique, 418 p.
MARTIN, J., 1967, Cours de mathématiques pour la préparation aux brevets de techniciens supérieurs et pour les écoles d'ingénieurs, Paris, Dunod, XVIII-722 p.
MARTIN Philippe, 1997, Structures hiérarchiques dans le karst de la Sainte Baume (B. du Rh, Var ; France) 12e Congrès de spéléologie, Symposium 7, Vol.1, Union internationale de spéléologie et Société suisse de spéléologie éditeurs, p.129-132.
MARTIN, Philippe, 2003a, « Construire un objet géographique. Recherche d'une méthodologie. » in Objets et indicateurs géographiques sous la direction de J. MABY, Collection Actes Avignon n°5, Université d'Avignon et UMR ESPACE 6012 du CNRS éditeurs, p.42-88, 13 fig., 1 graphe. Texte en ligne sur les sites : http://www.umrespace.org et http://www.geo.univ-avignon.fr.
MARTIN, Philippe, 2003b, « Objectivation des formes en géographie et calculs d'indicateurs fractals. Exemples karstiques. » in Objets et indicateurs géographiques sous la direction de J. MABY, Collection Actes Avignon n°5, Université d'Avignon et UMR ESPACE 6012 du CNRS éditeurs, p.153-268, 13 fig., 1 graphe. Texte en ligne sur les sites : http://www.umrespace.org et http://www.geo.univ-avignon.fr.
MARTIN, Philippe, 2003c, « Les limites en géographie physique. Eléments de réflexion », Travaux de l'Institut de géographie de Reims, « Frontières, limites et continuité », Reims, vol. 29, n°113-114, p. 127-143.
MARTIN, Philippe, 2004a, « La forme peut-elle libérer la prisonnière du carrefour ?, in Géopoint 2004, Avignon, p. 19-39.
MARTIN, Philippe, 2004b, Modélisation fractale et structurelle des formes en géographie. Réflexion développée à partir d'exemples karstiques, 3 tomes, Avignon, HDR, 169 p., 314 p., 179 p.
MARTIN Philippe, 2005, (sous la direction de VOLVEY A.), Géométrie fractale et géographie : l'exemple des formes physiques. in Echelles et temporalités, Atlande, Paris, p. 65-71.
MARTIN, Philippe. 2006a, La forme peut-elle libérer la prisonnière du carrefour ? Vers une théorie de la forme en géographie. Colloque Géopoint 2004 : La forme en géographie, Avignon, Groupe Dupont et UMR ESPACE 6012 du CNRS éditeurs, p. 19-38.
MARTIN, Philippe, 2006b, La dimension fractale d'un relief varie-t-elle avec l'altitude ? L'exemple de l'Aigoual (France). Colloque Géopoint 2004 : La forme en géographie, Avignon, Groupe Dupont et UMR ESPACE 6012 du CNRS éditeurs, p. 327-332.
MARTIN, Philippe, 2006c, Des courbes de niveau fractales « scale dependent » à l'Aigoual (France) ? Mesure et signification d'une courbure. Colloque Géopoint 2004 : La forme en géographie, Avignon, Groupe Dupont et UMR ESPACE 6012 du CNRS éditeurs, p. 333-340.
MARTIN, Philippe, 2006d, Fractale parabolique et fractale « scale dependent » : Un problème de courbure ? Echelle et finitude. Colloque Géopoint 2004 : La forme en géographie, Avignon, Groupe Dupont et UMR ESPACE 6012 du CNRS éditeurs, p.341-352.
MARTIN, Philippe, 2006e, Colloque Géopoint 2004 : La forme en géographie, Avignon juin 2004, Synthèse du thème 3 (atelier 2) : L'instrumentation pour la reconnaissance et la construction des formes en géographie ; de la carte à la morphologie mathématique. p.383-390, Groupe Dupont et UMR ESPACE 6012 du CNRS éditeurs.
MARTIN, Philippe, 2006f, Les limites du temps et la géographie de demain. Colloque Géopoint 2006 : Demain la géographie, Avignon, Groupe Dupont et UMR ESPACE 6012 du CNRS éditeurs, Brouillons Dupont, p.37.
MARTIN, Philippe, 2006g, Ne faudrait-il pas renaturaliser la géographie ? Colloque Géopoint 2006 : Demain la géographie, Avignon, Groupe Dupont et UMR ESPACE 6012 du CNRS éditeurs, Brouillons Dupont, p.81.
MARTIN, Philippe, 2006h, Caractérisation fractale du relief « stationnarisé » du Lodevois. Colloque SAGEO 2006, Cdrom ISBN : 2-9526014-1-0, Laboratoire : Image et ville et Université L. Pasteur, Strasbourg éditeur, 23 p., 7 fig.
MARTIN, Philippe, à paraître - Approche fractale des Grands Causses (Massif Central, France). Structure spatiale de la relation existant entre l'altitude et la dimension fractale de courbes de niveau covariantes. Actes des Journées de l'Association Française de Karstologie de Sion (Suisse), Université de Lausanne éditeur.
MATHIS, Philippe (s.d.), 2003, Graphes et réseaux. Modélisation multiniveau, Paris, Lavoisier, 362 p.
MAYET, Laurent, « L'émergence d'une nouvelle science ? », Sciences et avenir, « L'énigme de l'émergence, HS n°143, juillet-août 2005, p. 5.
Merveilles des châteaux des Flandres, d'Artois, de Picardie et du Hainaut, 1973, Paris, Hachette, 286 p. [Librairie hachette et société d'étude et de publications économiques]
MESSIAH, Albert, 1959, Mécanique quantique, 2 tomes, Paris, Dunod, XVI-974 p.
MOLK, Jules (s.d.), 1991, Encyclopédie des sciences mathématiques pures et appliquées, tome IV, Paul APPELL (s.d.), La mécanique, volume 1, Généralités. Historique, Sceaux, Editions Jacques Gabay, 292 p. [Les grands classiques Gauthier-Villars]
MURRAY R., Spiegel, 1980, Analyse de Fourier et application aux problèmes de valeurs aux limites, trad. Romain JACOUD, Paris, Série Shaum, 200 p.
MURRAY R., Spiegel, 1986, Transformée de Laplace, trad. Romain JACOUD, Paris, Série Schaum, 272 p.
MURRAY R., Spiegel, 1992, Variables complexes, trad. fr., Paris, Série Schaum, 314 p.
NAIMARK, Mark Aronovich, 1962, Les représentations linéaires du groupe de Lorentz, trad. G. LOCHAK, Paris, Dunod, XII-372 p.
NICOLAS-OBADIA, Georges, 1980, « Passer outre et se retrouver », in Géopoint 1980. Axiomes ou principes en géographie, Avignon, Groupe Dupont, 212 p.
NOTTALE, Laurent, 1993, Fractal space-time et microphysics. Towards a theory of scale relativity, World scientific, Singapour, XIV-338 p.
NOTTALE, Laurent, 1998, La relativité dans tous ses états. Au-delà de l'espace-temps, Paris, Hachette, 320 p.
NOTTALE, Laurent 2001a, « Relativité d'échelle. Structure de la théorie », in : Objets d'échelles, Revue de synthèse, n°1, T.122, p. 11-25.
NOTTALE, Laurent, 2001b, « Relativité d'échelle et morphogenèse », in Objets d'échelles, Revue de synthèse, n°1, T.122, p. 93-116.
NOTTALE, Laurent, 2002a, « Relativité d'échelle, non différentiabilité et espace-temps fractal », in ABRY, p., GONCALVES, p. et LEVY VEHEL, J., Traité IC2, volume n°2, « Lois d'échelle, fractales et ondelettes », Chapitre 7, Hermès Lavoisier, 234 p.
NOTTALE, Laurent, 2002b, « La relativité d'échelle », in Réda BENKIRANE, La Complexité, vertiges et promesses. 18 histoires de sciences, Paris, Le Pommier, p. 331-356.
NOTTALE, Laurent, CHALINE, Jean, GROU, Pierre, 2000, Les arbres de l'évolution. Univers, vie, sociétés, Paris, Hachette, 380 p.
NOTTALE, Laurent, CHALINE, Jean, GROU, Pierre, 2002, Evolution morphologique et culturelle humaine : l'apport des modèles fractales, http://wwwusr.obspm.fr/~nottale/
arGNCaix.pdf, 12 p.
ODIFREDDI, Piergiorgio, 2004, Les mathématiques à l'aube du XXIe siècle, trad. Simoca COCCO et Rémi MONASSON, Paris Belin, 176 p. [Regards sur la science]
[OMT] Ondelettes, multifractales et turbulences de l'ADN aux croissances cristallines, 1995, ARNEODO, Alain, ARGOUL, Françoise, BACRY, Emmanuel, ELEZGARAY, Juan, MUZY, Jean-François, Paris, Diderot, 168-XXXIII p.
OSCHII, Mamoru, 1995, Ghost in the shell, Tokyo, Shirow Masamune/Kodansha LTD, 1h20''.
PARETO Vilfredo, 1896, Cours d'économie politique. In PARETO œuvres complètes. Réimpression Droz, Genève, 1965.
PEREC, George, 2000, Espèces d'espace, Paris, Galilée, 186 p.
PETITOT, Jean, 2004, Morphologie et esthétique. Maisonneuve & Larose éditeur, Paris, 374 p.
PHAM, Frédéric, 1996, Les différentielles, Paris, Masson, XIV-138 p.
POMIAN, Krzysztof, 1984, L'ordre du temps, Paris, Gallimard, 366 p.
POPPER, Karl, 1960, La logique de la découverte scientifique, trad. fr., Paris, Payot, 480 p.
POPPER, Karl, 1978, La connaissance objective, trad. fr., Bruxelles, Complexe, 176 p.
Pour la science, « Les chemins de la logique », n°49, 120 p.
PRIGOGINE, Ilya, 1994, Les lois du chaos, trad. fr., Paris, Flammarion, 126 p. [Champ 369]
PRIGOGINE, Ilya, 1996, La fin des certitudes. Temps, chaos et les lois de la nature, Paris, Odile Jacob, 224 p.
PRIGOGINE, Ilya, NICOLIS, Grégoire, 1992, A la rencontre du complexe, Paris, PUF, 382 p.
PRIGOGINE, Ilya, STENGERS, Isabelle, 1979, La nouvelle alliance. Métamorphose de la science, Paris Gallimard, 296 p.
PRIGOGINE, Ilya, STENGERS, Isabelle, 1992, Entre le temps et l'éternité, Paris, Flammarion, 222 p. [Champs 262]
PUMAIN, Denise, 2006, Hierarchy in natural and social sciences, Dordrecht, Springer, X-244 p. [Methodos series volume 3]
PUMAIN, Denise, SANDERS, Léna, SAINT-JULIEN, Thérèse, 1989, Villes et auto-organisation, Paris, Economica, 192 p.
PUMAIN, Denise, SAINT-JULIEN, Thérèse, 1997, L'analyse spatiale. Localisations dans l'espace, Paris, Armand Colin, 168 p. [Cursus géographie]
PUMAIN, Denise, SAINT-JULIEN Thérèse, 2001, Les interactions spatiales, Paris, Armand Colin, 192 p. [Cursus géographie]
RACINET, Philippe (s.d.), 1996a, Recherches pluridisciplinaires sur le terroir picard de l'époque antique à la Révolution française : Boves. Complexe castre et prioral du « Quartier Notre-Dame », Amiens.
RACINET, Philippe, 1996b, Recherches pluridisciplinaires sur un terroir picard de l'époque antique à la Révolution français. Boves, complexe castral et prioral du « Quartier Notre-Dame ». Dossier de programmation de fouilles, Amiens, SRA Picardie et Laboratoire d'histoire et d'archéologie de l'Université de Picardie, 78 p.
RACINET, Philippe, 1996c, Recherches pluridisciplinaires sur un terroir picard de l'époque antique à la Révolution français. Boves, complexe castral et prioral du « Quartier Notre-Dame ». Campagne 1996, Amiens, SRA Picardie et Laboratoire d'histoire et d'archéologie de l'Université de Picardie, 282 p.
RACINET, Philippe, 1997a, « Un centre de pouvoir et de peuplement : l'exemple de Boves [Somme] », in Aux sources de la gestion publique. Actes du colloque des 26 et 27 janvier 1997, t. 3, « Hommes de Pouvoir. Ressources et lieux de Pouvoir Ve-XIIIe siècles », MAGNOU-NORTIER, Elisabeth (Ed.), Septentrion, Lille, 314 p.
RACINET, Philippe, 1997b, Recherches pluridisciplinaires sur un terroir picard de l'époque antique à la Révolution français. Boves, complexe castral et prioral du « Quartier Notre-Dame ». Campagne 1997, Amiens, SRA Picardie et Laboratoire d'histoire et d'archéologie de l'Université de Picardie, 348 p.
RACINET, Philippe, 1998, Recherches pluridisciplinaires sur un terroir picard de l'époque antique à la Révolution français. Boves, complexe castral et prioral du « Quartier Notre-Dame ». Campagne 1998, Amiens, SRA Picardie et Laboratoire d'histoire et d'archéologie de l'Université de Picardie, 391 p.
RACINET, Philippe, 1999a, Recherches pluridisciplinaires sur un terroir picard de l'époque antique à la Révolution français. Boves, complexe castral et prioral du « Quartier Notre-Dame ». Campagne 1999, Amiens, SRA Picardie et Laboratoire d'histoire et d'archéologie de l'Université de Picardie, 242 p.
RACINET, Philippe, 1999b, Recherches pluridisciplinaires sur un terroir picard de l'époque antique à la Révolution français. Boves, complexe castral et prioral du « Quartier Notre-Dame ». Document final de synthèse. Campagnes 1996-1999, Amiens, SRA Picardie et Laboratoire d'histoire et d'archéologie de l'Université de Picardie, 395 p.
RACINET, Philippe, 2000, Recherches pluridisciplinaires sur un terroir picard de l'époque antique à la Révolution français. Boves, complexe castral et prioral du « Quartier Notre-Dame ». Campagne 2000, 2 tomes, Amiens, SRA Picardie et Laboratoire d'histoire et d'archéologie de l'Université de Picardie, 230 p., 435 p.
RACINET, Philippe, 2001, Recherches pluridisciplinaires sur un terroir picard de l'époque antique à la Révolution français. Boves, complexe castral et prioral du « Quartier Notre-Dame ». Campagne 2001, Amiens, SRA Picardie et Laboratoire d'histoire et d'archéologie de l'Université de Picardie, 350 p.
RACINET, Philippe, 2002a, Recherches pluridisciplinaires sur un terroir picard de l'époque antique à la Révolution français. Boves, complexe castral et prioral du « Quartier Notre-Dame ». Document final de synthèse. Campagnes 2000-2002, Amiens, SRA Picardie et Laboratoire d'histoire et d'archéologie de l'Université de Picardie, 408 p.
RACINET, Philippe, 2002b, Recherches pluridisciplinaires sur un terroir picard de l'époque antique à la Révolution français. Boves, complexe castral et prioral du « Quartier Notre-Dame ». Document final de synthèse. Campagnes 2003-2005, Amiens, SRA Picardie et Laboratoire d'histoire et d'archéologie de l'Université de Picardie, 168 p.
RACINET, Philippe, 2003, Recherches pluridisciplinaires sur un terroir picard de l'époque antique à la Révolution français. Boves, complexe castral et prioral du « Quartier Notre-Dame ». Campagne 2003, Amiens, SRA Picardie et Laboratoire d'histoire et d'archéologie de l'Université de Picardie, 212 p.
RACINET, Philippe, 2004a, « 1000 ans d'architecture dans le château de Boves », Archeologia, 414, p. 36-49.
RACINET Philippe (s.d.), 2004b, « Site castral de Boves du Xe au XVIIe siècle », Revue archéologique de Picardie, Hors série.
RACINET, Philippe, 2004c, « Un lieu de pouvoir exceptionnel aux portes d'Amiens : Boves (Xe-XIIe siècles) », in Lieux de pouvoir en Normandie et sur ses marges, Caen, Publications du CRAHM.
RACINET, Philippe, 2004d, Recherches pluridisciplinaires sur un terroir picard de l'époque antique à la Révolution français. Boves, complexe castral et prioral du « Quartier Notre-Dame ». Campagne 2004, Amiens, SRA Picardie et Laboratoire d'histoire et d'archéologie de l'Université de Picardie, 219 p.
RACINET, Philippe, 2006, « Un lieu de pouvoir exceptionnel aux portes d'Amiens : Boves (Xè – XIIè siècles) », in Lieux de pouvoir en Normandie et sur les marges. A. M. FLAMBARD HERIDIER (Dir.). Publications du Centre de Recherches Archéologiques et Historiques Médiévales (CRAHM), Caen, 256 p.
RACINET Philippe, DROUIN Lionel, 2002, « De la résidence carolingienne à la motte : le complexe castral et prioral de Boves (somme, France), des IXe-Xe au XIIIe siècle ». in Château – Gaillard, colloque de Gwatt, Publications Centre de Recherches Archéologiques et Historiques Médiévales (CRAHM), Caen, 312 p.
RACINET, Philippe, RACINET, Sabine, 2000, « Le siège de Boves en 1185 », in NIVET Philippe (s.d.), La bataille en Picardie, combattre de l'Antiquité au XXe siècle, Amiens, Encrage.
RACINET, Philippe, SCHWERDROFFER, Joël (coord.), 2004, Méthodes et initiations d'histoire et d'archéologie, Paris, Edition du temps, 382 p.
RAFFESTIN, Claude, 1980, « Remarques incertaines sur l'axiomatisation en géographie », in Géopoint 1980. Axiomes ou principes en géographie, Avignon, Groupe Dupont, p. 136-145.
REVEL, Jacques (s.d.), 1996, Jeux d'échelles. La micro-analyse à l'expérience, Paris, Gallimard, 244 p.
Revue de synthèse. Objets d'échelles, 2001, Paris, Centre international de synthèse Albin Michel, 254 p.
RICŒUR, Paul, 1984, 1985, Temps et récits, 3 tomes, Paris, Le Seuil, 1983, 320 p., 234 p., 428 p.
RICŒUR, Paul, 2000, La mémoire, l'histoire, l'oubli, Paris, Le Seuil, 408 p. [Points E468]
RUELLE, David, 1991, Hasard et chaos, Paris, Odile Jacob, 248 p.
SALCH, Charles-Laurent, 1979, Dictionnaire des châteaux et des fortifications du Moyen Age en France, Strasbourg, XVI-1288 p.
SANDERS, Léna, 1989, L'analyse statistique des données en géographie, Montpellier, Reclus, 268 p. [Alidade]
SANDERS, Léna (s.d.), 2001, Modèles en analyse spatiale, Paris, Lavoisier, 334 p.
SAPOVAL, Bernard, 1997, Universalités et fractales Paris, Flammarion, 276 p.
SCHRODINGER, Erwin, 1986, Qu'est-ce que la vie ? De la physique à la biologie, trad. Léon KEFFLER, Paris, Le Seuil, 236 p. [Sciences 94]
SCHRODINGER, Erwin, 1992, Physique quantique et représentation du monde, trad. fr., Paris, Le Seuil, 186 p. [réédition de 1935] [Sciences 78]
SCHWARTZ, Laurent, 1961, Méthodes mathématiques pour les sciences physiques, Paris, Hermann, 392 p.
Sciences et avenir, « L'énigme de l'émergence », HS n°143, 84 p.
SCHROEDER, Manfred, 1991, Fractals, chaos, powers laws. Minute from an infinite paradis, Freeman editor, New York, 430 p.
SMIRNOV, Vladimir, Cours de mathématiques supérieures, trad. fr., 3 tomes, 4 volumes, Moscou, Mir, 1969, 498 p., 672 p., 694 p., 328 p.
SOBER, Elliot, « Ni élan vital ni réductionnisme », Sciences et avenir, « L'énigme de l'émergence, HS n°143, juillet-août 2005, p. 10-13.
SORNETTE, Didier, 2000, Critical phenomena in natural sciences. Chaos, fractals, selforganization and disorder : concepts and tools. Springer éditeur, 434 p.
SORNETTE, Didier, 2003, Why stock markets crash. Critical events in complex financial systems. Princeton university press, Princeton & Oxford, 421 p.
STEWART, Ian, 1998, Dieu joue-t-il aux dés ? Les mathématiques du chaos, trad. Marianne ROBERT et Marcel FILOCHE, Paris, Flammarion, VIII-602 p. [Champ 411]
STEWART, Robert, 1997, Les idées qui ont changé le monde, trad. fr., Paris, Solar, 224 p.
Tangente, « Ces formes qui nous fascinent », n°106, septembre-octobre 2005, 52 p.
TANNIER, Cécile, PUMAIN, Denise, 2005, « Fractals in urban geography : a theoretical outline and an empirical example », in Cybergeo, n°303, 22 p.
THOM, René, 1974, Modèles mathématiques de la morphogenèse, Paris, Union générale des éditions, 320 p. [collection 10-18 n°887]
THOM, René, 1983, Paraboles et catastrophes, Paris, Flammarion, 190 p.
THOM, René, 1991, Esquisse d'une sémiophysique. Physique aristotélicienne et théorie des catastrophes, Paris, InterEditions, 272 p.
TRICOT, Claude, 1980, « L'axiomatique en mathématiques », in Géopoint 1980. Axiomes ou principes en géographie, Avignon, Groupe Dupont, p. 22-30
VARELA, Francisco, 2002, « Autopoïese et émerge », in Réda BENKIRANE, La Complexité, vertiges et promesses. 18 histoires de sciences, Paris, Le Pommier, p. 161-176.
VIDAL, Christian, DEWEL, Guy, BORCKMANS, Pierre, 1994, Au-delà de l'équilibre, Paris, Hermann, 372 p.
VOLVEY, Anne (s.d.), 2005, Echelles et temporalités, Paris, Atlande, 240 p.
WACKERMANN, Gabriel, 2005, Dictionnaire de géographie, Paris, Ellipses, 432 p.
WHITE, Robert, 1998, « Cities and cellular automata », Discrete dynamics in Nature and Society n°2, p. 111-125.
WHITE, Robert, ENGELEN, George, 1993, « Cellular automata and fractal urban form : a cellular modelling approach to the evolution of urban land use patterns », Environment and planning A, Planning & Design n°25, p. 1175-1199.
WHITE, Robert, ENGELEN, George, 1997, « Cellular automata as the basis of integrated dynamic regional modeling », Environment and planning B, Planning & Design n°24, p. 235-246.
[WW] WONNACOTT, Thomas H., WONNACOTT, Ronald J., 1995, Statistique. Economie – Gestion – Sciences – Médecine, trad. Patrick COHENDET, Maurice LETHIELLEUX, Mohamed LYAZID, Anne-Marie RICHARDOT et Gérard SCHADE, Paris, Economica, 920 p.
ZIPF, George Kingsley, 1932, Selective studies and the principle of relative frequency in language.
ZIPF, George Kingsley, 1935, Psycho-biology of languages, Houghton-Mifflin.
ZIPF, George Kingsley, 1941, National unity and disunity. The nation as a bio-social organism, Bloomington Indiana, Principia Press.
ZIPF, George Kingsley, 1949, Human behavior and the principle of least effort, Addison-Wesley.
ZWIRN, Hervé P., 2006, Les systèmes complexes. Mathématiques et biologie, Paris, Odile Jacob, 220 p.
Notes
[1] Stephen Jay Gould voit le terme au sens large puisqu'il y inclut la philosophie.
[2] Il ne s'agit pas d'un reproche mais d'un constat.
[3] C'est une animation japonaise.
[4] Nom donné par James Yorke. Le chaos devient un objet mathématique avec une signification et un statut bien précis.
[5] Ici, le vecteur est, par défaut, un vecteur à trois dimensions, matérialisant les trois directions de l'espace euclidien.
[6] Le quadrivecteur est le nom particulier donné au vecteur de l'espace-temps, possédant quatre composantes.
[7] Attention. Il ne faudra pas confondre l'analyse fractale et l'analyse des formes fractales. La première est une véritable analyse au sens de René Descartes qui est appelé analyse non standard fractale. La seconde est une méthode analytique particulière qui permet de « mesurer » les formes fractales.
[8] Les forces extérieures sont les forces sortant du système, tandis que les forces intérieures sont les forces entrant ou évoluant à l'intérieur du système.
[9] Attention. Ici, μ correspond à un indice, et pas à une puissance.
[10] Rappelons que le traitement complet à cinq dimensions reste à faire.